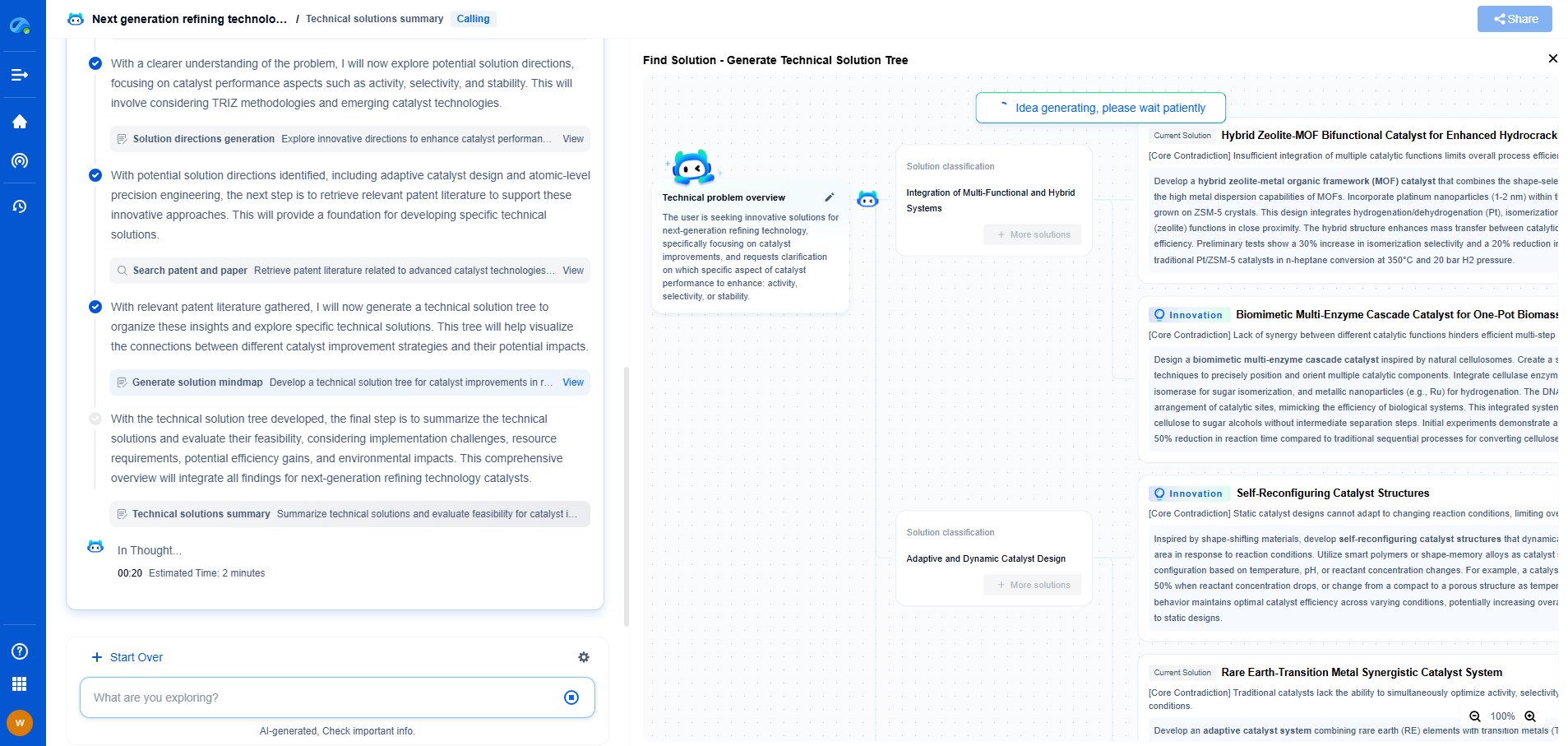
Improving Control Accuracy with State Estimation Techniques
JUL 2, 2025 |
In today's rapidly evolving technological landscape, precision and accuracy in control systems have become paramount. From autonomous vehicles to robotics and industrial automation, the need for precise control is crucial to ensure safety, efficiency, and reliability. One of the most effective ways to enhance control accuracy is through state estimation techniques. By providing a more accurate representation of the system's current state, state estimation plays a critical role in improving the performance of control systems.
Understanding State Estimation
State estimation involves using mathematical algorithms to estimate the internal states of a system based on available measurements. These internal states are often not directly measurable, making state estimation essential for obtaining a complete picture of the system's dynamics. The process typically involves filtering noisy measurements, predicting future states, and correcting these predictions with actual measurements. Two widely used state estimation techniques are the Kalman Filter and Particle Filter.
The Kalman Filter: A Proven Approach
The Kalman Filter is a powerful tool for state estimation, particularly in linear systems with Gaussian noise. It operates in a two-step process: prediction and update. During the prediction step, the filter uses a mathematical model to predict the next state of the system. In the update step, it gathers data from sensors to adjust the predicted state, effectively minimizing the error. The Kalman Filter is widely used in applications where high precision is required, such as aerospace and navigation systems.
Particle Filter: Tackling Nonlinear Challenges
While the Kalman Filter is effective for linear systems, many real-world applications involve nonlinear dynamics. The Particle Filter is designed to handle such complexities by employing a set of random samples, or "particles," to represent the probability distribution of the system's state. Each particle is assigned a weight based on how well it matches the observed data. Through iterative processes of sampling, weighting, and resampling, the Particle Filter converges towards an accurate estimation of the system's state. This technique is particularly useful in robotics and computer vision, where environments can be highly unpredictable.
Improving Control Accuracy with State Estimation
Incorporating state estimation techniques into control systems significantly enhances their accuracy and reliability. By providing real-time insight into the system's state, these techniques enable more informed decision-making. For instance, in autonomous vehicles, accurate state estimation allows for precise control of speed, direction, and obstacle avoidance, reducing the risk of accidents. In industrial automation, it ensures that machinery operates within optimal parameters, minimizing downtime and enhancing productivity.
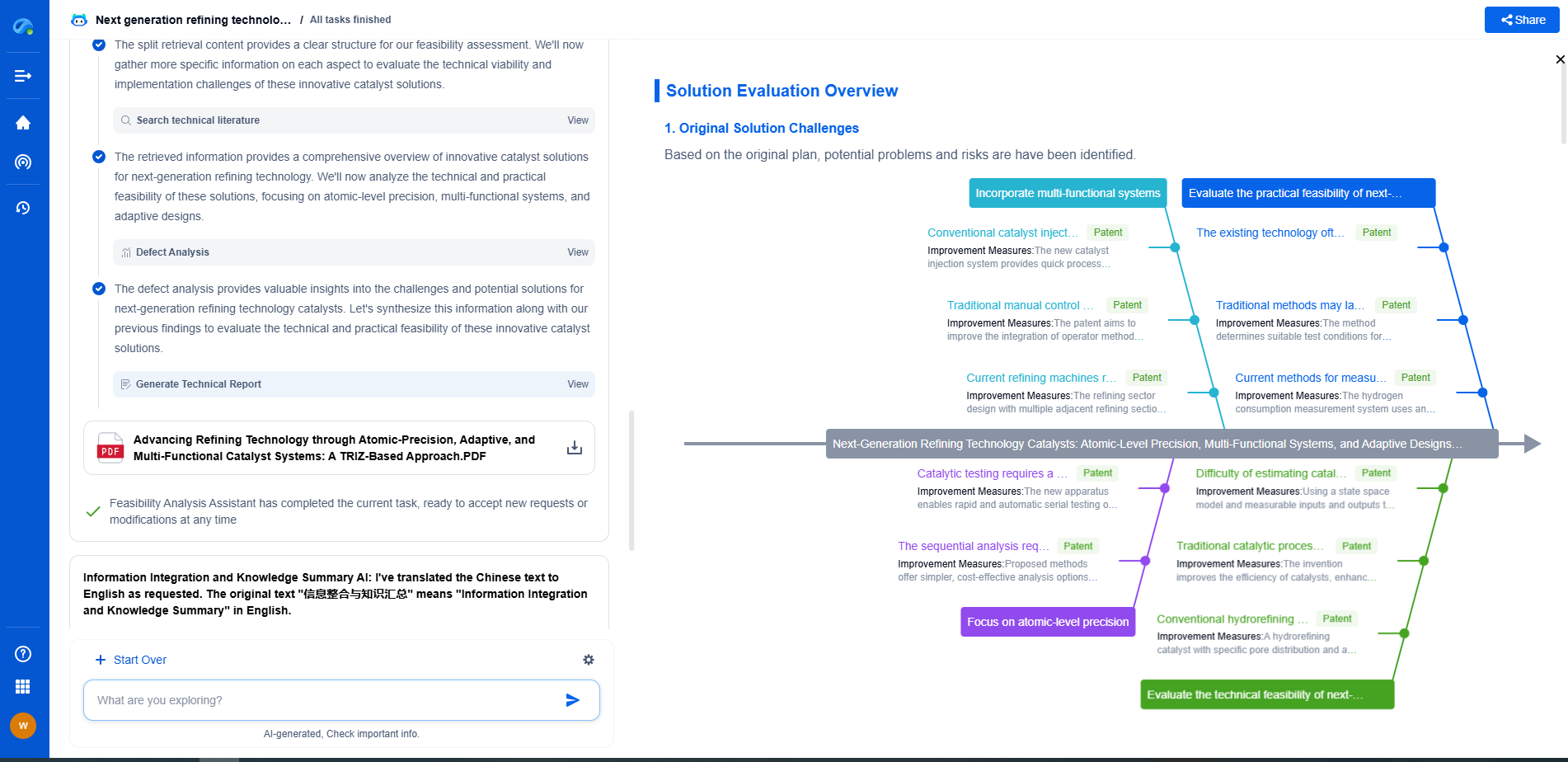
Challenges and Considerations
While state estimation techniques offer substantial benefits, they are not without challenges. The accuracy of state estimation depends on the quality of the models and measurements used. Inaccurate models or noisy data can lead to errors in estimation, potentially compromising the control system's performance. Additionally, computational complexity can be a concern, especially in systems with high-dimensional state spaces. It is crucial to balance the need for precision with the available computational resources to ensure efficient operation.
Future Directions
As technology continues to advance, the development of more sophisticated state estimation techniques is likely to follow. Machine learning and artificial intelligence are poised to play a significant role in this evolution, offering new ways to model complex systems and process large volumes of data. By integrating these technologies, future state estimation methods will likely become more robust, adaptable, and capable of handling an even wider range of applications.
Conclusion
State estimation techniques are indispensable in modern control systems, providing the accuracy and reliability needed for safe and efficient operation. From the simplicity of the Kalman Filter to the versatility of the Particle Filter, these methods offer valuable tools for navigating the complexities of real-world dynamics. As we continue to push the boundaries of technology, the importance of precise control, supported by advanced state estimation, will only grow, paving the way for smarter, more autonomous systems.
Ready to Reinvent How You Work on Control Systems?
Designing, analyzing, and optimizing control systems involves complex decision-making, from selecting the right sensor configurations to ensuring robust fault tolerance and interoperability. If you’re spending countless hours digging through documentation, standards, patents, or simulation results — it's time for a smarter way to work.
Patsnap Eureka is your intelligent AI Agent, purpose-built for R&D and IP professionals in high-tech industries. Whether you're developing next-gen motion controllers, debugging signal integrity issues, or navigating complex regulatory and patent landscapes in industrial automation, Eureka helps you cut through technical noise and surface the insights that matter—faster.
👉 Experience Patsnap Eureka today — Power up your Control Systems innovation with AI intelligence built for engineers and IP minds.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com