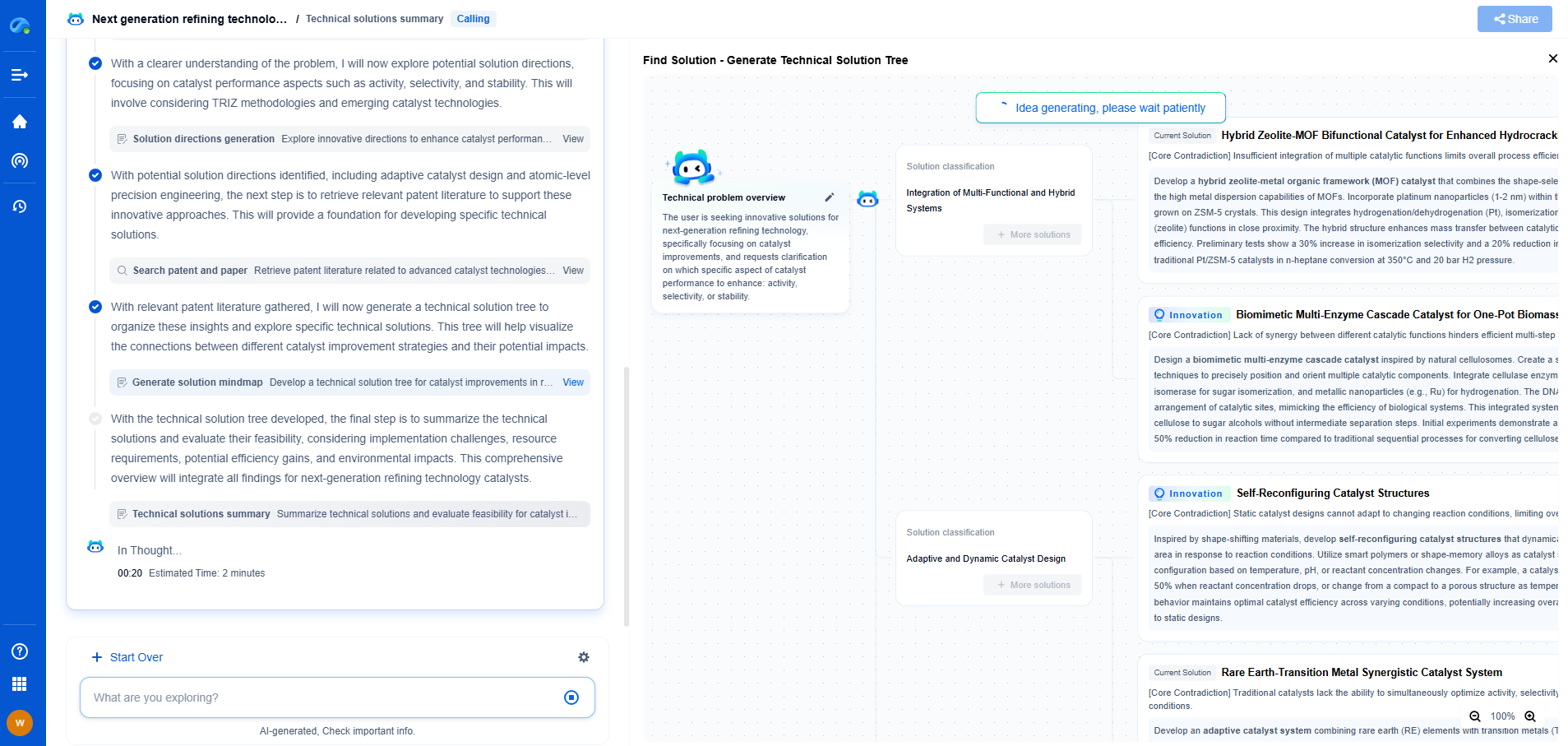
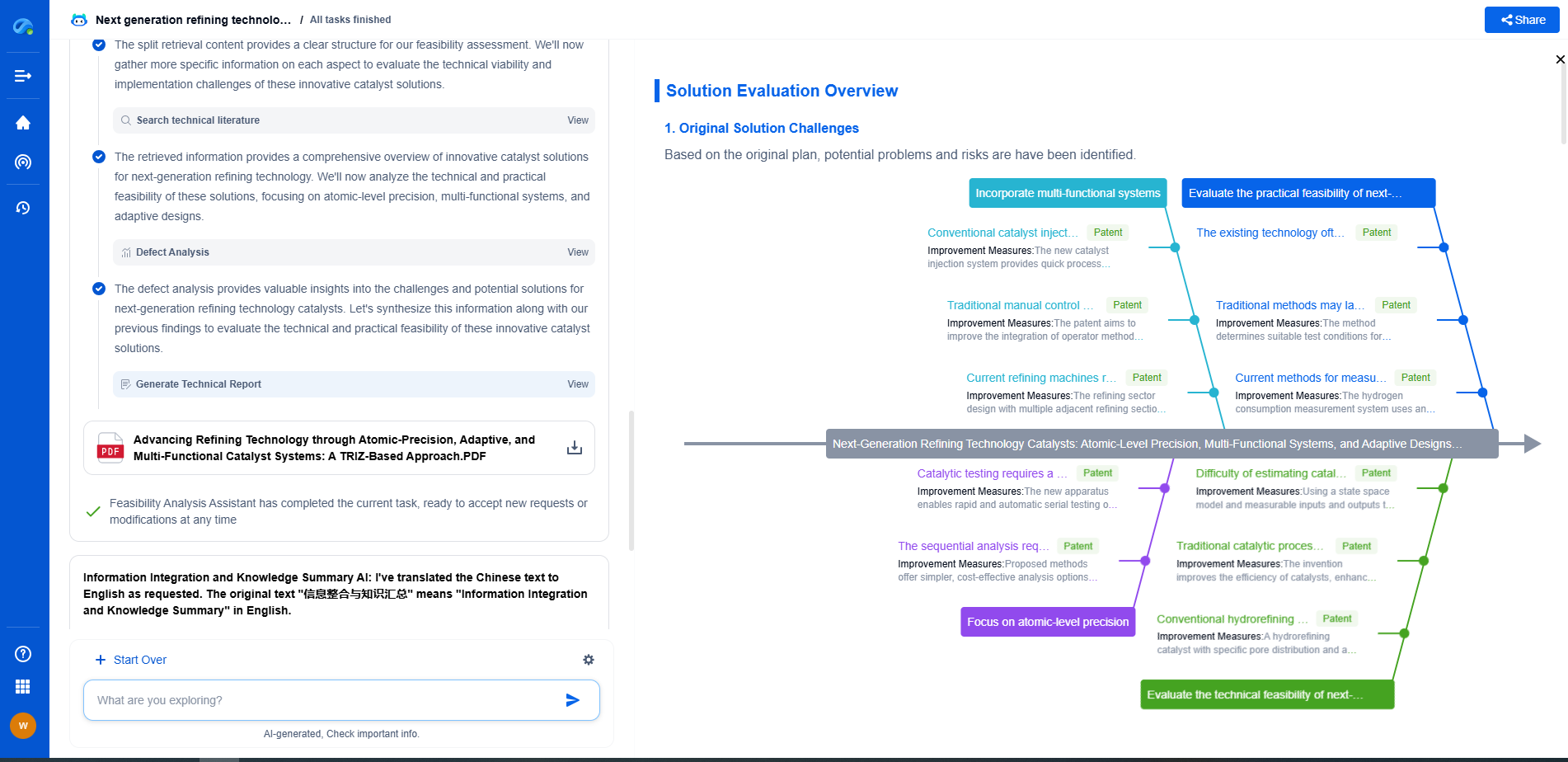
Langmuir adsorption model: Basics and relevance to filter media
JUL 25, 2025 |
The Langmuir adsorption model is a cornerstone in the field of surface chemistry and materials science. Developed by Irving Langmuir in 1916, this model describes the adsorption of molecules on a solid surface, providing essential insights into how molecules interact with surfaces. Its simplicity and effectiveness make it highly relevant in analyzing how filter media work, especially in capturing unwanted particles or molecules from a fluid phase.
Fundamentals of the Langmuir Model
The Langmuir model is based on a few key assumptions that make it applicable to a variety of adsorption scenarios. First, it assumes that the surface is homogeneous, meaning that all adsorption sites are equivalent. Additionally, it posits that adsorption is limited to a single monolayer and that there are no interactions between adsorbed molecules. The adsorption process is also considered to be in dynamic equilibrium, with the rate of adsorption equaling the rate of desorption.
The mathematical representation of the Langmuir isotherm is expressed as:
q = (q_max * b * P) / (1 + b * P)
where q is the amount of adsorbate on the adsorbent, q_max is the maximum adsorption capacity, b is the Langmuir constant related to the affinity between the adsorbate and adsorbent, and P is the pressure (or concentration in case of solutions).
Relevance to Filter Media
Filter media are materials that separate particles or molecules from fluids, and understanding their efficiency is crucial for a wide range of applications, from water purification to air filtration. The Langmuir model helps in comprehending how these media capture pollutants, as it provides insights into the saturation point and the efficiency of the filter material.
In practical terms, the Langmuir model can predict the capacity of a filter media to adsorb a specific pollutant. By determining the Langmuir constants for a given system, engineers can design filter media with optimized properties for maximum adsorption efficiency. This is particularly useful in creating filters that need to remove specific contaminants from water or air, such as heavy metals, dyes, or volatile organic compounds.
Applications in Modern Filtration Technology
The application of the Langmuir model extends beyond theoretical analyses. In modern filtration technology, it aids in the development of novel materials such as activated carbons, zeolites, and metal-organic frameworks. These materials are engineered to have specific pore sizes and surface characteristics that align with the assumptions of the Langmuir model, thus maximizing their adsorption capacities.
For instance, in water treatment processes, activated carbon filters designed using Langmuir model parameters can efficiently remove organic compounds and chlorine. Similarly, in air purification technologies, zeolites designed with Langmuir principles can selectively adsorb and trap volatile organic compounds, improving air quality.
Limitations and Considerations
While the Langmuir model provides valuable insights, it is not without limitations. Real-world surfaces are often not homogeneous, and the presence of multiple layers of adsorbate can complicate the adsorption process. Additionally, interactions between adsorbed molecules can occur, especially at high coverage, which the Langmuir model does not account for.
Despite these limitations, the Langmuir model remains a fundamental tool in the initial stages of filter media design. Researchers often use it in conjunction with other models, such as the Freundlich or BET isotherms, to gain a more comprehensive understanding of adsorption processes.
Conclusion
The Langmuir adsorption model continues to be a vital framework in the study and application of filter media. Its ability to provide a simplified yet informative description of adsorption phenomena makes it a staple in scientific research and industrial applications. By understanding and applying the principles of the Langmuir model, engineers and scientists can design more effective and efficient filtration systems to meet the growing demands for clean air and water.
From next-generation membrane materials to high-efficiency separation processes for pharmaceuticals, water treatment, food processing, or energy systems, the filtration & separation industry is rapidly evolving with a surge in material innovation, microstructure design, and process optimization.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
Whether you're designing the next high-throughput filter, optimizing nanostructured surfaces, or exploring new separation media for emerging industries—Patsnap Eureka gives you AI-driven insights in seconds, helping you move from ideation to innovation with confidence.
🚀 Start your free trial today and experience how Eureka transforms filtration innovation—from reactive to predictive.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com