
Introduction to Binary and Decimal Systems
Understanding the binary and decimal systems is crucial for anyone working with numbers in mathematics and computing. The binary system (base-2) uses only 0 and 1, forming the foundation of digital computing. In contrast, the decimal system (base-10) uses digits 0 to 9 and is widely used in daily life. This article will guide you through the process of converting binary to decimal, explain their key differences, and highlight their applications in modern technology. Whether you’re a student or a professional, mastering binary to decimal conversions is an essential skill in today’s digital world.

Steps for Binary to Decimal Conversion
Converting a binary number to its decimal equivalent involves a straightforward process based on the positional value of each digit. Follow these steps:
Step 1: Write Down the Binary Number
Note the binary number you want to convert, ensuring that each digit is clearly positioned from right to left.
Step 2: Assign Positional Values
Assign powers of 2 to each digit, starting from ![]() for the rightmost digit and increasing the power by one as you move left. For example, in the binary number 1101, the positional values are
for the rightmost digit and increasing the power by one as you move left. For example, in the binary number 1101, the positional values are ![]()
Step 3: Multiply Each Binary Digit by Its Positional Value
Multiply each binary digit (0 or 1) by its corresponding power of 2. For example, for the binary number 1101 : 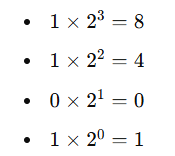
Step 4: Sum Up the Results
Add all the results from step 3 to get the decimal equivalent. In this example:
8+4+0+1=13
Step 5: Verify the Conversion
Double-check your calculations to ensure accuracy.
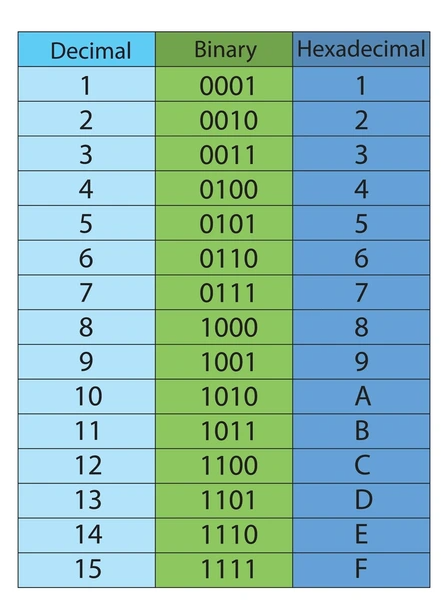
Using Tools for Binary to Decimal Conversion
Decimal Arithmetic Units
Modern processors often include dedicated hardware units to handle binary to decimal conversion. These units perform the conversions seamlessly during operations like multiplication and division, optimizing speed and reducing power consumption.
Optical Computing
Emerging technologies, such as optical computing, are exploring all-optical binary to decimal converters. These use devices like Mach-Zehnder interferometers to achieve ultra-fast conversions. Optical systems are promising for applications requiring high bandwidth and speed.
Recent Innovations
Scaled Remainder Tree
This innovative algorithm replaces traditional division with multiplications in the critical path. It can achieve significant speed improvements, up to 50%, over conventional methods like those in the GMP (GNU Multiple Precision Arithmetic Library).
Efficient Encoding Techniques
Encoding methods like B-transform reduce the bit length of binary expressions, enhancing compression performance for uniformly distributed data. These techniques are particularly useful in data storage and processing applications.
Applications of Binary to Decimal in Computing
Why Accurate Data Conversion Matters
Computers process information in binary, but many systems require data in a form that humans can easily understand. Industries like finance, engineering, and database management often rely on numerical formats for precise calculations. Standards such as IEEE 754 ensure these calculations meet the demands of modern applications.
Efficient Conversion Methods
A popular approach involves dividing numbers repeatedly by 10 to generate readable digits. Techniques like weighted-sum functions and radix-based arithmetic decompositions also play a significant role. Advanced solutions, such as CORDIC algorithms, offer optimized and precise results for demanding applications.
The Role of Hardware in Fast Data Processing
Hardware solutions ensure faster and more accurate transformations compared to software-based approaches. Tools like look-up tables, adders, and multipliers provide the foundation for many systems. Cutting-edge processors, including IBM’s System z series, feature dedicated arithmetic units for enhanced performance. Innovations such as pipelining and parallel architectures further improve speed and reliability.
New Applications Driving Innovation
Accurate number conversion is critical for evolving technologies in areas like finance, scientific research, and online computing. Innovative fields, such as optical systems, use advanced encoding techniques to handle transformations across different formats. These developments demonstrate the growing need for efficient and reliable solutions across industries.
To get detailed scientific explanations of binary to decimal, try Patsnap Eureka.

