
Introduction
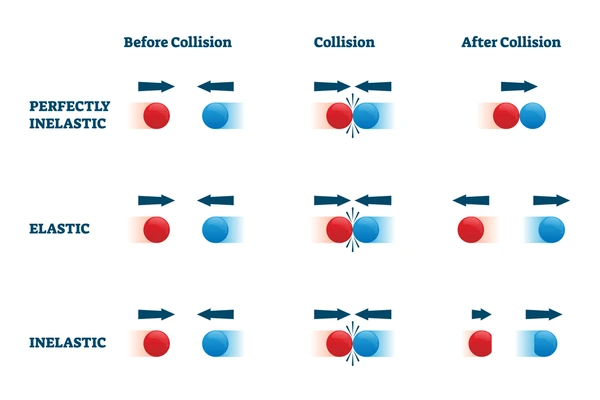
In physics, collisions are categorized into two main types: elastic and inelastic collisions. These collisions describe how objects interact and transfer momentum and energy when they collide. The key difference lies in the behavior of kinetic energy—elastic collisions conserve it, while inelastic collisions lose some energy as heat, sound, or deformation. In this guide, we’ll explore Elastic vs. Inelastic Collisions, breaking down their definitions, properties, and real-world examples to help you understand how they work in nature and technology.
What is an Elastic Collision?
An elastic collision occurs when particles interact without losing total kinetic energy or momentum. During these events, the target atom usually stays in its ground state without excitation. This interaction often causes the projectile to deflect significantly, altering the path of fast-moving charged particles as they pass through a material. The energy transferred to the target atom appears as recoil, playing a crucial role in determining the stopping power in nuclear physics and related applications. Elastic collisions are vital for understanding particle dynamics in various scientific and engineering contexts.
Fundamental Principals
Elastic Collisions:
Elastic collisions preserve both kinetic energy and momentum, making them unique in their energy efficiency. These interactions cause no permanent deformation or heat generation. The primary governing equations include:
- Momentum Conservation:
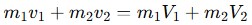
- Kinetic Energy Conservation:
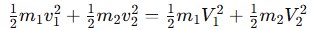
These principles are essential in applications involving particle collisions, billiards, and atomic interactions, where energy preservation is critical.

What is an Inelastic Collision?
An inelastic collision occurs when part of the kinetic energy converts into other forms, such as heat, sound, or deformation. Unlike elastic collisions, where the total kinetic energy remains unchanged, inelastic collisions result in energy loss, though momentum is still conserved. These collisions are further categorized as partially inelastic or completely inelastic. In a completely inelastic collision, the objects stick together after impact, moving as a single unit. This unique behavior highlights the diverse outcomes of energy transformations during inelastic interactions.
Fundamental Principles
Inelastic Collisions:
Inelastic collisions are characterized by the partial loss of kinetic energy, transformed into heat, sound, or deformation energy. Despite this, momentum remains conserved. The fundamental equation for these interactions is:
- Momentum Conservation:
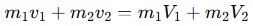
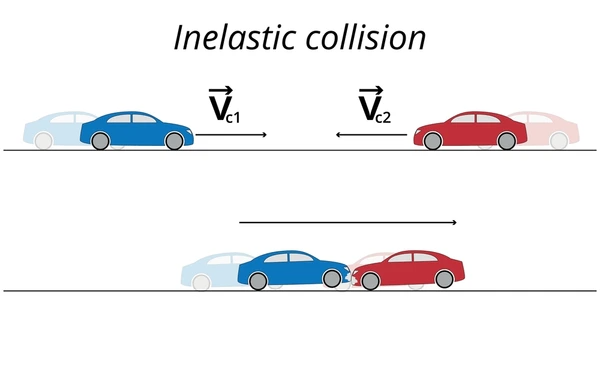
Elastic vs. Inelastic Collisions: Key Differences
Energy Transfer Mechanisms
- Elastic Collisions:
In elastic collisions, kinetic energy is exchanged between the colliding bodies without any loss to other forms of energy. For example, in proton-proton interactions, the elastic nature enables precise analysis of fundamental particles, ensuring no energy dissipates into heat or deformation. This property is vital in fields like particle physics and accelerator experiments. - Inelastic Collisions:
Inelastic collisions involve a partial transformation of kinetic energy into internal energy, leading to effects like photon creation. This phenomenon is crucial in cosmological studies, such as analyzing the Cosmic Microwave Background (CMB). In automotive contexts, energy is absorbed by safety features like airbags and crumple zones during inelastic collisions, ensuring passenger protection.
Practical Examples and Applications
- Elastic Collisions:
These interactions are commonly observed in atomic and subatomic processes, where energy conservation aids in studying particle behavior. For instance, elastic collisions of charged particles with atoms are essential in radiation physics, influencing particle trajectories in different materials. - Inelastic Collisions:
Inelastic collisions frequently occur in real-life scenarios, such as car accidents where energy absorption protects occupants. These collisions are also significant in material science, leading to plastic deformation and alterations in the mechanical properties of materials.
Mathematical Modelling and Simulation
- Elastic Collisions:
Mathematical models for elastic collisions often use scattering theory and central potential approximations to predict outcomes. For example, Rutherford’s scattering formula is a classic model that describes the behavior of particles during elastic collisions with a nucleus. - Inelastic Collisions:
Modeling inelastic collisions requires advanced techniques to account for energy dissipation and internal changes. Simulations often integrate competing rates for inelastic processes like charge or spin exchange, ensuring accurate predictions of system dynamics.
Experimental Observations and Ratios
- Elastic Collisions:
Experimental data frequently highlight the dominance of elastic collisions under specific conditions. For instance, in magnetic traps at low energy, the elastic-to-inelastic collision ratio can exceed 100, showcasing the efficiency of energy conservation. - Inelastic Collisions:
Observations reveal that inelastic collisions cause significant energy redistribution. This can include phenomena like Hawking radiation production or insights into dark matter and dark energy through photon creation, emphasizing their role in cutting-edge physics research.
Recent Innovations and Research
Recent advancements have significantly expanded our understanding of collision dynamics across various conditions. For instance, studies on ultracold quasi-two-dimensional gases reveal that laser confinement can enhance the elastic-to-inelastic collision ratio. This breakthrough offers new opportunities to control collision behaviors at low temperatures, which is vital for quantum simulations and precision experiments.
Another intriguing development is the discovery of “super-elastic” collisions. In these interactions, the restitution coefficient exceeds unity due to thermal fluctuations, seemingly defying traditional energy conservation principles. This phenomenon sheds light on the unique behaviors of small systems, paving the way for novel applications in nanotechnology and advanced materials research.
Conclusion: Elastic vs. Inelastic Collisions
Understanding Elastic vs. Inelastic Collisions is essential to grasp how energy and momentum behave during impacts. Elastic collisions conserve both momentum and kinetic energy, while inelastic collisions only conserve momentum, with kinetic energy lost in the process.
From molecular interactions in gases to vehicle crash safety, these concepts are key in explaining phenomena across physics and engineering. By recognizing their differences, you’ll gain deeper insights into the fundamental principles governing motion and collisions.
FAQs
- What is the main difference between elastic and inelastic collisions?
In elastic collisions, both momentum and kinetic energy are conserved. In inelastic collisions, momentum is conserved, but kinetic energy is lost. - Can a collision be partially elastic?
Yes, most real-world collisions are partially elastic, where some kinetic energy is lost, but objects don’t stick together. - Is momentum always conserved in collisions?
Yes, momentum is conserved in all types of collisions as long as no external forces act on the system. - Why is kinetic energy lost in inelastic collisions?
Kinetic energy is transformed into other forms like heat, sound, or deformation in inelastic collisions. - Are there real-world examples of perfectly elastic collisions?
Perfectly elastic collisions rarely occur in the real world but are common at the molecular and atomic levels, like gas molecule interactions.
To get detailed scientific explanations of elastic vs. inelastic collisions, try Patsnap Eureka.

