
Instantaneous velocity describes the velocity of an object at a specific point in time. Unlike average velocity, which measures the overall displacement over a time interval, instantaneous velocity focuses on a particular moment. It is crucial in understanding real-world motion, from projectile motion to circular motion. This article explores the definition, calculation, and applications of this velocity.
What is Instantaneous Velocity?
Instantaneous velocity refers to the velocity of an object at a given point in time. It is a vector, meaning it has both magnitude (speed) and direction. The formula for it is: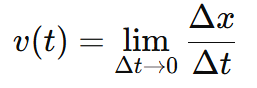
Where:
- v(t) = Instantaneous velocity at time
- Δx = Change in position
- Δt = Change in time
Instantaneous velocity provides a detailed view of motion at any point.

Instantaneous Velocity vs. Average Velocity
| Aspect | Instantaneous Velocity | Average Velocity |
|---|---|---|
| Time Frame | Specific moment in time | Over a time interval |
| Quantity | Vector (magnitude + direction) | Vector (magnitude + direction) |
| Calculation | Derivative of position with respect to time | Total displacement divided by total time |
| Dependence on Motion | Describes detailed motion at any time | Provides general motion information over time |
How to Calculate Instantaneous Velocity?
You can calculate instantaneous velocity by differentiating the position function x(t) with respect to time: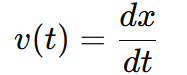
For example, for uniform motion with velocity v=10 m/s, the position function is:![]()
The instantaneous velocity is constant: ![]()
For accelerated motion, where the position function is ![]() , the instantaneous velocity is:
, the instantaneous velocity is:![]()
Thus, the velocity increases over time due to the acceleration.
Graphical Representation
A position vs. time graph helps visualize this concept. The slope of the tangent at any point represents velocity. For constant motion, the slope stays the same, indicating constant velocity. For accelerated motion, the slope changes, so velocity varies.
Real-World Applications
💡 Wondering about the real-world applications of instantaneous velocity? Eureka Technical Q&A provides clear explanations of how this concept is used in fields like physics, engineering, and automotive design, helping you apply it effectively to solve practical problems and optimize performance.
- Projectile Motion
This concept is crucial for understanding projectile motion, as it describes the velocity at any moment during the trajectory. By breaking it into horizontal and vertical components, we can predict the motion more precisely.Example: In basketball, players analyze the velocity at key moments to adjust their shots for accuracy. - Vehicle Motion
Automotive systems, such as adaptive cruise control and collision avoidance, use this principle to adjust vehicle speed in real-time based on velocity data.Example: Self-driving cars use sensors to track velocity, ensuring safe navigation without human input. - Space Exploration
In orbital mechanics, spacecraft rely on this concept to adjust their paths. Knowing velocity at specific times helps engineers navigate satellites and spacecraft accurately.Example: NASA’s Mars missions use velocity calculations to guide spacecraft to their landing sites. - Sports Science
Tools like motion capture track the velocity of athletes during various activities, helping optimize techniques in sports like running, swimming, and cycling.Example: Sprinters analyze their velocity during races to refine their technique and improve performance.
Key Factors Influencing Velocity
- Forces
Forces like gravity and friction influence velocity. These forces affect both speed and direction over time. - Acceleration
Acceleration, or the rate of change of velocity, impacts how fast the velocity increases or decreases. - Path Shape
The shape of an object’s path also plays a role. Curves cause velocity to change in both direction and magnitude.
Conclusion
Velocity at any given time is essential for understanding and analyzing motion. It plays a critical role in various fields like vehicle dynamics, space exploration, and sports science. By mastering this concept, we gain deeper insights into both theoretical and applied physics.
FAQs
1. How is instantaneous velocity different from average velocity?
It is the speed and direction at a specific time, while average velocity is the total displacement divided by the total time.
2. Can this velocity be negative?
Yes, when an object moves in the opposite direction, the value becomes negative.
3. How do you calculate it from a position vs. time graph?
You find the slope of the tangent line at a specific point on the graph to calculate velocity.position at that specific moment.
To get detailed scientific explanations of Instantaneous Velocity, try Patsnap Eureka.


