
Technical Background and Objectives
Background
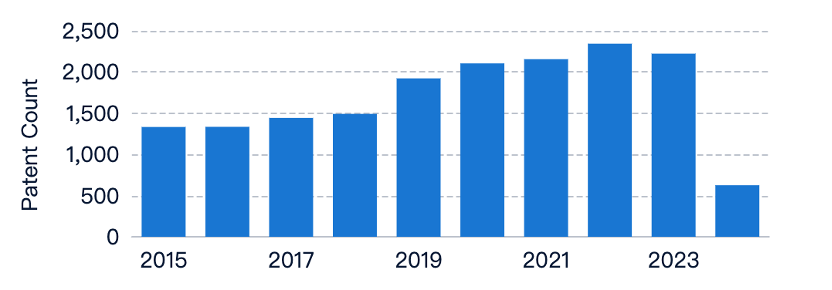
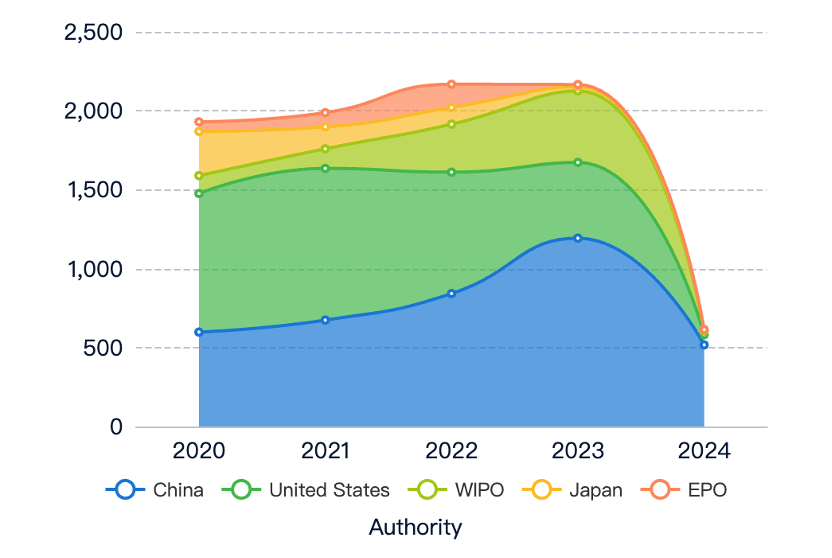
Patent applications related to reducing intensity error through linear interpolation have steadily risen, indicating growing interest and investment. While academic research has gained traction, it appears to have stabilized, suggesting a possible shift in research focus or maturation of theoretical foundations. The continued rise in patent applications, despite stable literature numbers, suggests that practical applications and commercialization efforts remain active.
Objectives
The primary objective is to develop innovative and efficient linear interpolation techniques that reduce intensity errors across various applications. This research aims to quantify the benefits, optimize algorithms, and develop application-specific solutions to improve the overall accuracy and effectiveness of linear interpolation methods.
To get a detailed scientific explanations of Linear Interpolation, try Eureka.
Technical Current Status Analysis
Linear Interpolation Overview
Linear interpolation is widely used in image processing, signal processing, computer graphics, and scientific computing. It estimates the value of a function or data point between two known points, crucial in reducing intensity errors.
Applications and Impact:
- Image Processing: Used in image resizing, scaling, and resampling to estimate new pixel values and reduce artifacts.
- Medical Imaging: Applied in CT and MRI to reconstruct images, reducing intensity errors and artifacts for more accurate images.
- Computer Graphics: Employed in texture mapping, anti-aliasing, and rendering for smoother transitions and reduced visual artifacts.
- Scientific Computing and Data Analysis: Essential in curve fitting, data smoothing, and numerical integration, improving computation accuracy.
Technical Characteristics and Challenges:
- Linearity Assumption: Assumes a linear relationship between known data points, which may not hold for all data types, leading to potential inaccuracies.
- Continuity and Smoothness: Ensures continuity but not higher-order smoothness, resulting in visible discontinuities with non-linear data.
- Accuracy and Error Bounds: Dependent on data point spacing; larger gaps or rapid changes increase interpolation errors.
- Computational Efficiency: Generally efficient but can be a bottleneck in real-time or large datasets; optimization is necessary.
- Higher-Dimensional Interpolation: Introducing complexities, especially with irregularly spaced data points.
Technological Paths:
- Adaptive and Non-Linear Interpolation: Combining linear interpolation with spline, polynomial, or machine learning-based methods.
- Error Analysis and Error-Bounded Interpolation: Quantifying and controlling interpolation errors through theoretical and numerical approaches.
- Parallel and Distributed Interpolation: Leveraging multi-core processors, GPUs, or distributed frameworks for acceleration.
- Higher-Dimensional Techniques: Efficient algorithms for higher-dimensional data with irregular spacing.
- Application-Specific Optimizations: Tailoring techniques to domain-specific constraints and data characteristics.
Research Content
Research Objectives
Investigate the effectiveness of linear interpolation in reducing intensity errors across various applications, develop optimized algorithms, and tailor them to specific use cases.
Research Direction and Focus
Theoretical Foundations
- Analyze the mathematical properties, assumptions, and limitations of linear interpolation.
- Compare linear interpolation with alternative methods under various conditions.
Empirical Evaluation
- Conduct controlled experiments in signal processing, image analysis, and data visualization.
- Quantify the effectiveness of linear interpolation in reducing intensity errors across different datasets.
Algorithm Optimization
- Develop optimized algorithms tailored to specific applications, focusing on error estimation and adaptive sampling.
- Enhance computational efficiency and resource constraints handling.
Application-Specific Studies
- Collaborate with domain experts to address real-world challenges in medical imaging, remote sensing, and telecommunications.
- Demonstrate potential benefits and facilitate adoption in various industries.
Technical Development Roadmap
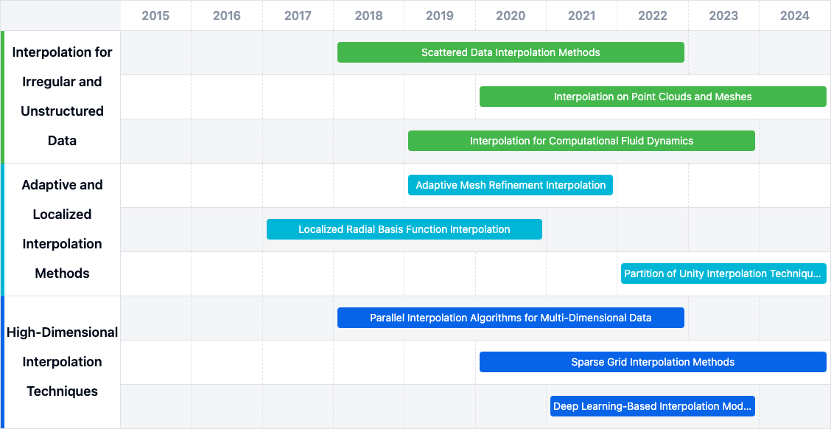
Key Areas of Advancement
- High-Dimensional Interpolation: Developing parallel algorithms for multi-dimensional data, sparse grid interpolation, and deep learning models.
- Adaptive and Localized Methods: Adaptive mesh refinement, localized radial basis function interpolation, and partition of unity techniques.
- Irregular and Unstructured Data: Scattered data interpolation, point clouds, and computational fluid dynamics applications.
Main Player Analysis
Key Players and Focus
- Shenzhen University: Image processing and computer vision, leveraging linear interpolation in deep learning models.
- University of Leeds: Archeomagnetic intensity change inference using Bayesian algorithms and linear interpolation.
- Canon Inc.: Image processing and digital imaging systems, improving quality through interpolation.
- Sony Group Corp.: Digital imaging and video processing, enhancing accuracy and quality.
- Southeast University: Image processing, signal processing, and scientific computing, focusing on error reduction and accuracy improvement.
Current Technical Solution Overview
Linear Interpolation Error Correction
- Techniques: Correcting errors to enhance accuracy, including specific algorithms and optimization methods.
- Hardware Implementations: Circuits and devices for efficiency and accuracy.
- Image and Video Processing: Techniques for improving visual quality in image scaling, resizing, and motion compensation.
- Numerical Control Systems: Minimizing errors in motion control and positioning systems.
Linear Interpolation Hardware Implementations
- Architectures: Dedicated circuits, FPGA-based systems, and specialized processors.
- Error Reduction Techniques: Estimation, correction methods, and high-precision algorithms.
- Image Processing: EfficiencyDive into the world of innovative linear interpolation methods to minimize intensity errors in a wide range of applications. Quantify advantages, fine-tune algorithms, and create customized solutions for optimal accuracy. in image tasks, considering edge detection and motion compensation.
- Signal Processing: Real-time capabilities for digital signal interpolation and data streams.
Linear Interpolation Algorithms and Methods
- Algorithms for Reducing Intensity Errors: Optimizing performance and precision in various applications.
- Efficient Algorithms: Reducing computational complexity and memory requirements.
- Combining Linear and Non-Linear Techniques: Enhancing accuracy and smoothness.
Linear Interpolation in Motion Control and Positioning
- Motion Compensation: Techniques for estimating and compensating motion between frames.
- Adaptive Filtering: Adjusting filters based on motion characteristics.
- Motion Vector Interpolation: Improving accuracy in motion estimation.
- Systems for Accurate Motion Trajectories: Ensuring smooth motion in industrial robots and controllers.
- Occlusion Handling: Managing occlusions and disocclusions in motion-compensated interpolation.
Key Patent Interpretation
Patent Highlights
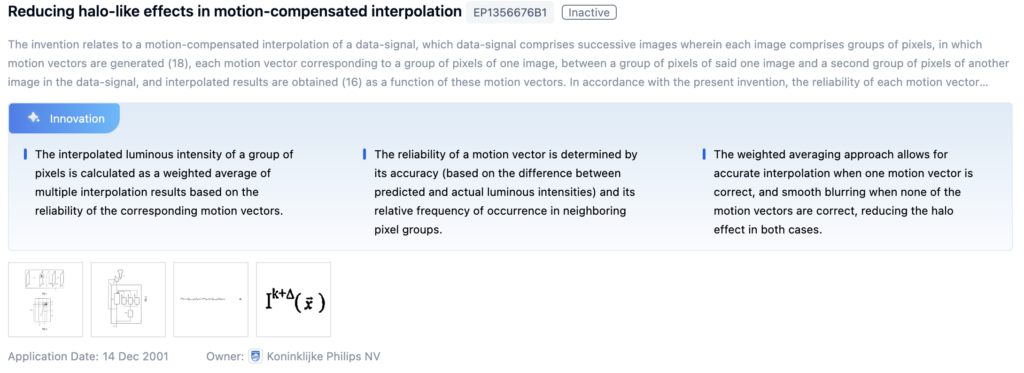
Patent 1: Reducing Halo-Like Effects in Motion-Compensated Interpolation
- Core Invention Points:
- Reliability estimation of motion vectors.
- Weighted averaging based on vector reliability to reduce halo effects.
- Improved accuracy in motion-compensated interpolation.
Patent 2: High-Quality Gradient-Corrected Linear Interpolation for Demosaicing
- Core Invention Points:
- Gradient correction term computed using color information.
- Linear combination with prior interpolation for improved color estimates.
Patent 3: Pond Culture Dissolved Oxygen Missing Data Interpolation Method
- Core Invention Points:
- Integrating human-made activity data with environmental data.
- PCA and SSIM methods for constructing interpolation models.
Possible Research Directions
- Linear Interpolation Error Correction: Techniques to minimize errors and improve accuracy.
- Hardware Implementations: Efficient circuits and devices for linear interpolation.
- Advanced Algorithms: Optimizing interpolation processes for various applications.
- Multi-Dimensional Techniques: Addressing complexities in higher-dimensional data.
- Application-Specific Uses: Tailoring techniques to specific domains like image processing, signal processing, and motion control.
If you want an in-depth research or a technical report, you can always get what you want in Eureka Technical Research. Try now!

