
What are Ground State Electron Configurations?
The ground state electron configurations of elements reveal how electrons are arranged in an atom’s orbitals when it is in its lowest energy state. This foundational concept is essential for understanding an element’s chemical behavior, reactivity, and bonding tendencies. In this article, we explore the principles for determining ground state electron configurations, highlight key rules and exceptions, and examine their connection to the physical and chemical properties of elements. Whether you’re studying the periodic table or analyzing chemical reactions, understanding ground state electron configurations is crucial for grasping the science behind elemental properties.
Principles Governing Electron Configurations
The ground state electron configuration is determined based on several fundamental principles:
- Aufbau Principle: Electrons fill orbitals starting from the lowest energy level to the highest. This principle dictates the order in which orbitals are filled.
- Pauli Exclusion Principle: No two electrons in an atom can have the same set of four quantum numbers. This principle ensures that each orbital can hold a maximum of two electrons with opposite spins.
- Hund’s Rule: Electrons will fill degenerate orbitals (orbitals with the same energy) singly before pairing up. This minimizes electron-electron repulsion within an atom.
For example, the ground state electron configuration for lithium (Li) is 1s²2s¹. This configuration is determined by filling the 1s orbital first, followed by the 2s orbital.
Identifying Exceptions to Standard Rules
While the above rules generally apply, there are notable exceptions, particularly among transition metals and heavier elements. These exceptions often arise due to the relative energies of the orbitals and electron-electron interactions. For instance:
- Chromium (Cr): Instead of the expected [Ar] 4s² 3d⁴, the actual configuration is [Ar] 4s¹ 3d⁵. This is because a half-filled d-subshell (3d⁵) provides extra stability.
- Copper (Cu): Instead of [Ar] 4s² 3d⁹, the configuration is [Ar] 4s¹ 3d¹⁰, as a fully filled d-subshell (3d¹⁰) is more stable.
How to Write Ground State Electron Configurations
The ground state electron configuration of an element describes the distribution of electrons in the atomic orbitals. The general procedure involves:
- Identifying the number of electrons: This is equal to the atomic number of the element.
- Filling the orbitals: Electrons are placed in orbitals following the Aufbau principle, which states that electrons occupy the lowest energy orbitals first.
- Using the Pauli Exclusion Principle: Each orbital can hold a maximum of two electrons with opposite spins.
- Applying Hund’s Rule: Electrons will fill degenerate orbitals (orbitals with the same energy) singly before pairing up.
For example, the ground state electron configuration for lithium (atomic number 3) is 1s² 2s¹. This configuration follows the Aufbau principle, filling the 1s orbital first and then the 2s orbital with the remaining electron.
Chunking Strategy for Teaching Electron Configurations
A chunking strategy can be an effective tool for teaching electron configurations, especially for students at the higher secondary level. This method involves breaking down the process into manageable chunks and using mnemonics to aid memory. For example, students can learn the order of orbital filling using the mnemonic “1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d 7p.”
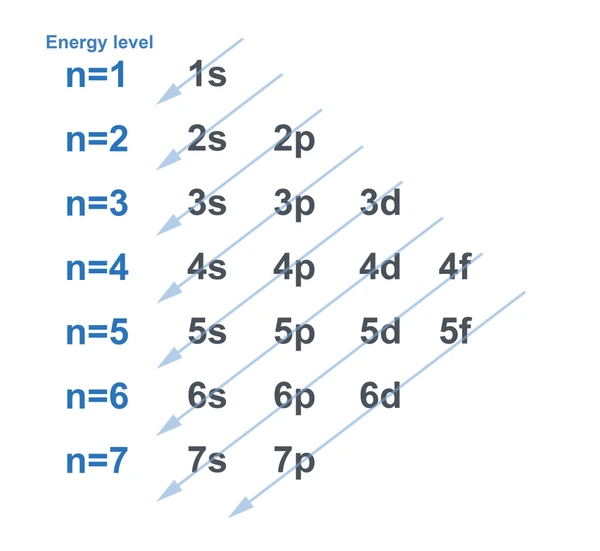
Applications of Ground State Electron Configurations
Chemical Reactions and Catalysis
Understanding electron configurations is crucial for predicting chemical reactions and designing effective catalysts. Valence electrons, which determine bonding and reactions, play a vital role in redox processes. For instance, writing accurate electron configurations helps explain electron transfers in reactions, aiding the development of catalysts that enhance reaction efficiency by facilitating these transfers.
Material Science and Engineering
Electron configurations are essential for studying the electronic properties of materials, particularly transition metals. These configurations explain properties like magnetism and conductivity in various materials. For example, research on Hubbard chains shows how electron arrangements influence behaviors like ferromagnetism or insulating properties, guiding the creation of advanced materials for electronics and spintronics.
Quantum Computing and Quantum Systems
Electron configurations play a pivotal role in quantum computing by representing the ground state of quantum systems. Preparing and refining ground states is fundamental for quantum simulations, as it ensures stability and low energy levels in quantum systems. These configurations drive advancements in quantum technologies and simulations.
Education and Pedagogy
Teaching electron configurations effectively requires strategies like chunking and mnemonics. These methods help students learn and recall configurations for elements, building a strong foundation in chemistry. Clear understanding of electron arrangements prepares students for more complex topics and advanced scientific concepts.
Theoretical and Computational Chemistry
Theoretical studies on electron distribution provide insights into orbital energies and configuration influences. These frameworks are crucial for computational chemistry, enabling accurate simulation of chemical systems. By modeling configurations, researchers can predict material behavior and chemical interactions more effectively.
Industrial Applications
Electron configurations guide material selection and process optimization in industries. For instance, in grounding systems for electrical substations, understanding configurations informs material choices for electrodes, improving current dissipation and fault protection. This knowledge enhances safety and efficiency in industrial processes.
Application Cases
| Product/Project | Technical Outcomes | Application Scenarios |
|---|---|---|
| Diamond and Triangle Hubbard Chains Study | Construction of exact ground states exhibiting properties such as flat-band ferromagnetism and correlation-induced behaviors. | Material science research focusing on electronic properties and phase transitions in quantum systems. |
| Ground State Electron Configuration for Lithium | Explanation of the electron-electron interaction energy affecting electron configurations. | Educational tools for teaching and understanding electron configurations in chemistry. |
| First-Row Transition Metals Electron Configurations | Qualitative analysis of factors influencing electron configurations in transition metals. | Educational exercises for undergraduate students in inorganic chemistry. |
| Quantum System Ground State Method Tencent Technology (Shenzhen) Co., Ltd. | Improved operability of quantum ground state solutions. | Quantum computing and advanced quantum technology applications. |
Latest Technical Innovations in Ground State Electron Configurations
Advancements in Quantum Computing
Quantum computers are transforming how we solve electronic structure problems, offering greater efficiency than classical methods. Techniques like the Variational Quantum Eigensolver (VQE) and Quantum Phase Estimation (QPE) are being refined to calculate ground state properties with remarkable precision. These innovations are paving the way for more accurate simulations in quantum chemistry and material science.
Enhancements in Density Functional Theory
Density Functional Theory (DFT) continues to dominate electronic structure calculations, with recent advancements improving its accuracy. The development of hybrid functionals, which blend DFT with Hartree-Fock methods, allows for better predictions of molecular properties. These enhancements are crucial for modeling complex systems and improving computational reliability.
Machine Learning in Quantum Chemistry
Machine learning is revolutionizing electronic structure predictions by integrating with traditional quantum chemistry techniques. Trained on extensive datasets, these models rapidly predict configurations for new systems, dramatically reducing computational demands. This approach enables faster insights into molecular properties while maintaining accuracy.
To get detailed scientific explanations of ground state electron configurations, try Patsnap Eureka.

