
What is interpolation?
Interpolation is a technique used to estimate values between known data points, constructing new points within a discrete dataset. It creates approximating functions that align with given data, enabling predictions and smooth transitions. Common methods include polynomial, spline, and trigonometric interpolation, chosen based on accuracy and application needs. Widely used in signal processing, image analysis, and scientific modeling, interpolation bridges gaps in data, ensuring continuity and precision across various fields.
Understanding Interpolation Techniques and Formulas
Interpolation estimates unknown values by constructing curves or functions based on known data points. It creates smooth transitions and ensures continuity in datasets. Here’s an overview of common techniques:
Linear Estimation
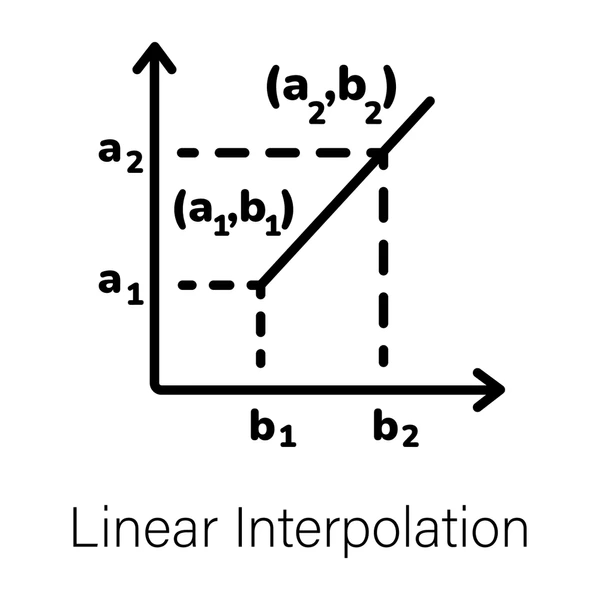
Linear estimation is the simplest method, drawing a straight line between two points. The formula is:
y = y1 + ((x – x1) / (x2 – x1)) * (y2 – y1).
This approach works best for datasets with minimal variation between points.
Polynomial Estimation
Polynomial techniques use equations of varying degrees to fit data points precisely. Popular methods include:
- Lagrange Method: A straightforward approach for fitting polynomials.
- Newton’s Method: Efficient for datasets with incremental additions.
- Neville’s Algorithm: Useful for iterative calculations.
Spline Estimation
Spline techniques create piecewise functions for better accuracy. Common options are:
- Cubic Splines: Ensures smoothness across data points.
- B-Splines: Offers flexibility and stability in fitting.
Trigonometric Estimation
This method uses sine and cosine functions to estimate values, often for periodic data or waveforms.
Multi-Dimensional Estimation
For datasets with multiple variables, bivariate and multivariate techniques provide accurate results. These methods handle complex relationships and high-dimensional data effectively.
Interpolation methods
Estimation involves approximating an unknown function, f(x)f(x), by constructing a function, IN(x)I_N(x), that passes through a given set of data points. Here’s an overview of popular methods:
- Polynomial Estimation
This method fits an (N−1)(N-1)th degree polynomial through NN data points. A well-known example is the Lagrange formula, which simplifies polynomial fitting for various datasets. - Piecewise Estimation
In this approach, different functions or polynomials are used over separate intervals. Common examples include piecewise linear estimation and cubic splines, which ensure smooth transitions between segments. - Trigonometric Estimation
This technique uses sines and cosines to approximate values, making it ideal for periodic data. It creates smooth and continuous functions across the dataset. - Multivariable Estimation
For datasets with multiple independent variables, this method helps analyze relationships in fields like image processing or climate modeling. - Radial Basis Function (RBF) Estimation
This approach uses radially symmetric functions based on distances between data points. It’s especially effective for irregular datasets. - Constrained Estimation
Advanced techniques like Hermite or Birkhoff methods account for derivatives at data points, ensuring smoothness and satisfying specific constraints.
Interpolation vs. Extrapolation
Defining Interpolation & Extrapolation
- Interpolation estimates values within the range of given data points. It constructs new points from discrete data, recreating a continuous signal. Popular methods include linear, polynomial, spline, and trigonometric techniques. This approach stays within observed data, making it more reliable and accurate.
- Extrapolation estimates values beyond the range of known data points. It predicts unknown values by extending observed trends or patterns. Methods like linear, polynomial, and conic extrapolation help make projections. However, extrapolation often carries more uncertainty and error risk due to limited data constraints.
Key Differences Between the Two Techniques
The primary distinction lies in their scope. While interpolation operates within observed data, extrapolation goes beyond it. Interpolation is typically more dependable because it works within the dataset’s boundaries. Extrapolation, though useful, requires caution as accuracy diminishes with increasing distance from known values.
Applications in Various Fields
Interpolation is commonly used in signal processing, image processing, and numerical analysis to fill gaps in data. Extrapolation, on the other hand, is employed for forecasting, trend analysis, and predictive modeling. Its effectiveness depends heavily on the strength and consistency of the underlying data trends.
When to Choose Each Approach
Interpolation is ideal for reconstructing missing data within observed ranges, ensuring accuracy. Extrapolation is better suited for predictions beyond existing data but should be approached cautiously. The choice depends on the problem at hand and the data’s scope, with interpolation often being the safer option.
Application Case of Interpolation
| Product/Project | Technical Outcomes | Application Scenarios |
|---|---|---|
| Adobe Photoshop | Using bicubic and bilinear interpolation for image resizing and transformations, resulting in high-quality image scaling while preserving details and minimizing artifacts. | Image editing software, graphic design, and digital photography workflows that require precise image manipulation and resizing. |
| MATLAB | Implementing various interpolation methods (linear, cubic spline, etc.) for data analysis, curve fitting, and numerical computations, enabling accurate function approximations and simulations. | Scientific computing, data analysis, and engineering applications that involve processing and visualizing complex data sets. |
| NVIDIA AI Upscaling | Leveraging deep learning and advanced interpolation techniques for upscaling and enhancing low-resolution images and videos, improving visual quality while preserving details. | Video processing, gaming, and multimedia applications that require real-time upscaling of visual content for better viewing experiences. |
| Digital Audio Workstations | Employing interpolation algorithms for sample rate conversion, enabling seamless audio playback and editing across different sample rates and resolutions. | Music production, audio engineering, and post-production workflows that involve manipulating and processing digital audio signals. |
| Medical Imaging Software | Using interpolation methods for image reconstruction, registration, and visualization in medical imaging modalities like CT, MRI, and ultrasound, enabling accurate diagnosis and treatment planning. | Healthcare applications, such as radiology, oncology, and surgical planning, where precise visualization and analysis of medical images are crucial. |
| Finite Element Analysis | Implementing interpolation techniques for mesh generation and numerical integration in finite element analysis, enabling accurate simulations of complex physical systems and structures. | Engineering simulations, structural analysis, and computational fluid dynamics applications that require precise modeling and analysis of physical phenomena. |
Latest Innovations of Interpolation
Personal PM2.5 Measurement
Researchers have developed advanced methods for monitoring personal PM2.5 levels, improving accuracy in air pollution exposure tracking. These innovations enhance data reliability and provide a clearer picture of individual environmental impacts.
Enhancing Image Scaling
New techniques, like multiplicative Lagrange methods, improve image quality during scaling for various display resolutions. These approaches reduce computational demands while delivering sharper, more detailed images, especially on high-definition screens.
Advancements in Video Coding
A modern picture prediction method leverages precise motion vectors and optimized filtering to simplify video coding. This technique minimizes memory usage and enhances compression efficiency, making video processing faster and more cost-effective.
Improvements in Computational Fluid Dynamics (CFD)
The multi-point momentum correction (IC) method offers better accuracy in CFD applications. By correcting edge velocities with surrounding data, this method improves numerical precision and speeds up convergence, solving common challenges in fluid dynamics.
Optimized Wireless Communications
A cubic spline method designed for wireless communications enhances signal processing by optimizing frequency-domain polynomials. It ensures better spectral performance while lowering implementation complexity and reducing latency in real-time applications.
Bridging Challenges Across Fields
These advancements demonstrate significant progress in fields like environmental monitoring, imaging, video processing, and signal transmission. By focusing on efficiency and precision, these methods address the specific needs of each application area effectively.
Technical Challenges
| Improved Interpolation for Image Scaling | Developing novel interpolation techniques to enhance image quality when resizing images for different display resolutions while reducing computational complexity. |
| Efficient Interpolation for Video Coding | Designing interpolation filtering methods that reduce memory operations and simplify the overall video coding process, leading to more efficient compression. |
| Advanced Interpolation for Computational Fluid Dynamics | Proposing alternative interpolation methods, such as the multi-point momentum interpolation correction technique, to improve numerical accuracy and convergence in computational fluid dynamics simulations. |
| Optimised Interpolation for Signal Processing | Developing optimised interpolation algorithms with improved spectral properties and reduced implementation complexity for signal processing applications in wireless communications. |
| Interpolation for CNC Machining | Enhancing curve fitting and optimal interpolation techniques for CNC machining, utilising methods like quadratic B-splines to improve accuracy and efficiency. |
To get detailed scientific explanations of interpolation, try Patsnap Eureka.

