Ionic bonding strength plays a crucial role in inorganic chemistry, particularly in understanding the behavior of ionic compounds. It refers to the energy released when gaseous ions come together to form a crystalline solid. Lattice energy helps explain key material properties like stability, melting point, solubility, and hardness. This article breaks down what this bond strength means, how it’s calculated, what influences it, and how it changes across the periodic table—with real-world examples and formulas included.
What is lattice energy? Eureka Technical Q&A explains that lattice energy is the amount of energy released when oppositely charged ions form a solid crystal lattice—reflecting the strength of ionic bonds and affecting properties like melting point and solubility.
Generate Ideas with Eureka AI
Get instant, smart ideas, solutions and spark creativity with Eureka AI. Generate professional answers in a few seconds.
Definition of Lattice Energy
Lattice energy is the energy released when one mole of an ionic crystalline solid forms from its gaseous ions under standard conditions.
General Equation:
M⁺(g) + X⁻(g) → MX(s) + Lattice Energy
This process is exothermic, meaning it releases energy. The greater the lattice energy, the stronger the ionic bond and the more stable the compound.
Importance of Lattice Energy
- Explains why salts form stable solids
- Helps compare ionic bond strength between compounds
- Influences solubility and melting point
- Crucial in thermodynamic calculations such as Born–Haber cycles
Factors Affecting Lattice Energy
1. Ionic Charge
The strength of ionic attraction increases with higher ion charges. Compounds with multiply charged ions, like Mg²⁺ and O²⁻ in MgO, typically exhibit stronger bonding forces than those with singly charged ions, such as Na⁺ and Cl⁻ in NaCl.
Example:
The bond strength in MgO is significantly higher than in NaCl due to the greater ionic charges involved.
2. Ionic Radius and Coordination Number
Smaller ions allow closer approach, resulting in stronger electrostatic interactions. Additionally, a higher coordination number—more neighboring ions—enhances overall stability.
Trend:
As ion size increases, the attraction between them weakens, lowering the cohesive force within the crystal.
3. Crystal Packing and Arrangement
The way ions are packed influences the overall energy of the solid. Denser packing or more symmetrical structures generally result in more stable configurations, although the impact varies depending on the compound.
4. Ion Size
Compact ions enable shorter distances between opposite charges, strengthening their attraction. Larger ions increase separation, weakening the force that holds the structure together.
5. Structural Geometry
The geometric arrangement of ions—whether in cubic, hexagonal, or other forms—affects how charges distribute throughout the structure. This variation can shift the total internal electrostatic potential.
6. Temperature Effects
In some crystals, thermal changes alter the stability of the ionic network. For example, in AB₂-type fluorite structures, thermal expansion can gradually reduce cohesive forces as temperature rises.
7. Electronic Excitations and Structural Defects
Exposure to high-energy radiation may cause localized excitations or form defects in the solid, temporarily or permanently weakening internal cohesion.
8. Engineered Compression or Expansion
Altering the spacing between ions through mechanical or chemical means—common in battery cathode design—can strengthen or weaken internal bonding depending on the direction of the change.
Lattice Energy Trends in the Periodic Table
| Compound | Ion Sizes | Lattice Energy (kJ/mol) |
|---|---|---|
| LiF | Small ions | High (~1046) |
| NaCl | Medium ions | Moderate (~787) |
| CsI | Large ions | Low (~600) |
| MgO | 2+ and 2− ions | Very High (~3795) |
Summary of Trends:
- Increases with charge on ions
- Decreases down a group (due to larger ionic radius)
- Increases across a period (due to smaller size and increased charge)
How to Calculate Lattice Energy
There are two main approaches:
1. Born–Haber Cycle
An indirect method using Hess’s law and thermodynamic data.
Steps involve:
- Sublimation of the metal
- Ionization of the metal
- Dissociation of nonmetal
- Electron affinity of the nonmetal
- Enthalpy of formation
- Lattice energy as the unknown
2. Born–Lande Equation (Theoretical Estimate)
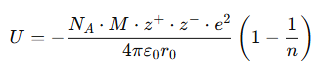
Where:
- U = lattice energy
= Avogadro’s number- M = Madelung constant (depends on crystal structure)
- z+,z−= charges on the cation and anion
-
= distance between ion centers - n = Born exponent (depends on ion compressibility)
Applications of Lattice Energy
Chemistry and Solid-State Physics
Scientists use this energy concept to understand the stability and reactivity of ionic compounds. It explains why some salts dissolve easily in water while others remain insoluble. In pharmaceutical research, these calculations help design stable co-crystals that improve drug delivery and formulation.
Energy Absorption and Structural Applications
Engineers design advanced structures to absorb crash impact energy in vehicles. These geometries reduce weight without sacrificing strength, enhancing crash performance. Additionally, they help with vibration control and shock damping, making them ideal for protecting delicate electronics.
Energy Conversion Technologies
New devices like the Lattice Energy Converter (LEC) can generate electricity from thermal or vibrational energy. This clean-tech innovation avoids radioactive materials and shows promise for future power systems. Researchers are also exploring similar structures to recover waste heat and boost system efficiency.
Materials Science and Engineering
3D printing technologies, such as laser powder bed fusion, allow for the creation of intricate structural frameworks. These are used in aerospace and biomedical applications where strength, lightness, and customization matter. Designs based on mathematical surfaces, like triply periodic minimal surfaces, deliver impressive stiffness and strength-to-weight ratios.
High-Energy Physics
Physicists apply these calculations in lattice field theory to explore particle behavior and fundamental forces. This research helps test predictions that go beyond the current Standard Model and deepen our understanding of the universe.
FAQs
Yes. It represents the energy released when the ionic solid forms, so it’s an exothermic process.
Because Mg²⁺ and O²⁻ have higher charges than Na⁺ and Cl⁻, resulting in stronger electrostatic attraction.
No. Lattice energy applies to ionic solids only. Covalent networks have different bonding models.
Often yes. If the energy required to break apart the crystal is too high, the compound may not dissolve easily in water.
Generally, higher lattice energy leads to a higher melting point due to stronger ionic bonds.
Conclusion
Lattice energy is a crucial concept that helps explain the stability and physical properties of ionic compounds. By understanding how ion size and charge influence lattice energy, chemists can predict trends in melting points, solubility, and bond strength. Whether calculated through a Born–Haber cycle or estimated with theoretical equations, lattice energy remains a key tool in modern chemical analysis and materials science.
To get detailed scientific explanations of lattice energy, try Patsnap Eureka.
