Poisson’s Ratio is a fundamental concept in material science and engineering, yet it often gets overlooked in favor of more familiar properties like tensile strength or elasticity. However, understanding Poisson’s Ratios is crucial for designing and analyzing materials and structures in fields such as civil engineering, aerospace, and biomechanics. This article explores the science behind Poisson’s Ratios, its practical applications, and why it is a key property in material design and analysis.
What is Poisson’s Ratio?
Poisson’s Ratio is defined as the ratio of lateral strain to axial strain when a material is stretched or compressed. When a material undergoes a deformation in one direction, it typically deforms in the opposite direction as well. Poisson’s Ratios quantifies this phenomenon, giving insight into how a material behaves under stress.
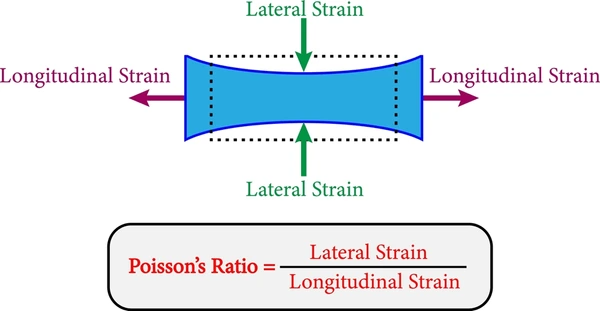
The formula is 
. Where ν is Poisson’s Ratio, lateral strain refers to deformation perpendicular to the applied load, and axial strain refers to deformation along the direction of the applied load.
Understanding the Behavior of Materials with Different Poisson’s Ratios
Materials exhibit different Poisson’s Ratios based on their composition and structure. These values typically range from 0 to 0.5 for most common materials. Materials with higher Poisson’s Ratios tend to be more ductile, while those with lower values are often stiffer.
Types of Materials and Their Poisson’s Ratios
- Metals: Poisson’s Ratios for most metals range between 0.25 and 0.35.
- Rubber: Poisson’s Ratio for rubber is close to 0.5, which means it deforms significantly in all directions under stress.
- Concrete: Poisson’s Ratio for concrete is usually lower, around 0.2, reflecting its stiffer nature compared to rubber.
Why is Poisson’s Ratio Important?
Poisson’s Ratio plays an important role in various material science and engineering applications. It helps engineers and researchers predict how materials will deform under different conditions, ensuring safer and more efficient designs.
Key Uses:
- Stress-Strain Analysis: Poisson’s Ratios is essential in analyzing how materials will react to applied forces, helping predict failure points in structures.
- Finite Element Analysis (FEA): Engineers use lateral strain ratio in FEA simulations to predict material behavior under different load conditions.
- Material Selection: Lateral strain ratio helps in selecting materials for applications where specific deformation behaviors are critical, such as in the automotive or aerospace industries.
The Influence of Poisson’s Ratio on Material Performance
💡 Need clarity on how Poisson’s ratio affects material performance? Eureka Technical Q&A offers in-depth explanations and practical insights into how Poisson’s ratio influences material behavior under stress, helping you select the right materials for your engineering projects.
Generate Ideas with Eureka AI
Get instant, smart ideas, solutions and spark creativity with Eureka AI. Generate professional answers in a few seconds.
- High Poisson’s Ratio (close to 0.5): Materials like rubber with high lateral strain ratio deform significantly in all directions. These materials are flexible, but they may not be ideal for load-bearing structures.
- Low Poisson’s Ratio (close to 0): Materials like cork or certain foams exhibit low lateral strain ratio. These materials are often lightweight and resistant to deformation, making them suitable for insulation or shock-absorbing applications.
Applications of Poisson’s Ratio in Various Industries
| Industry | Application | Key Parameter |
|---|---|---|
| Aerospace | Vibration-damping panels | ν = -0.5 to -2.0 1 |
| Biomedical | Vascular stents | Tunable ν via chiral cells |
| Construction | 3D-printed concrete | ν anisotropy = 0.15–0.25 12 |
| Electronics | Solder joints | ν = 0.3 assumed, but plastic strain varies by 20% with ν = 0.15–0.4 |
Civil Engineering:
In construction and infrastructure, Lateral strain ratio helps engineers predict how building materials like concrete, steel, and composites will behave under stress. The ratio is crucial for ensuring the durability and stability of bridges, buildings, and other structures.
Aerospace Engineering:
In aerospace, materials with specific Poisson’s Ratios are selected to ensure that aircraft components maintain structural integrity under extreme conditions. Understanding Poisson’s Ratios helps engineers design wings, fuselages, and other components that can withstand the forces encountered during flight.
Biomechanics:
Lateral strain ratio also has applications in biomechanics, particularly when analyzing biological tissues and implants. By understanding how tissues stretch or compress in response to mechanical forces, researchers can improve prosthetics, joint replacements, and other medical devices.
Performance Comparison: Materials with Different Poisson’s Ratios
| Material | Poisson’s Ratio | Characteristics | Best Use Case |
|---|---|---|---|
| Steel | 0.30 | Strong, ductile | Structural components |
| Rubber | 0.49 | Flexible, deformable | Shock absorption |
| Cork | 0.05 | Lightweight, resistant to compression | Insulation, packaging |
| Concrete | 0.20 | Stiff, durable | Construction |
Each material’s Poisson’s Ratio influences its selection for specific applications. Steel, for instance, offers a balance between strength and ductility, while rubber’s high lateral strain ratio makes it ideal for applications requiring flexibility.
Challenges and Limitations of Poisson’s Ratios
- Not Universally Accurate: For certain complex materials, especially composites, the standard lateral strain ratio may not accurately predict behavior under stress.
- Difficult to Measure in Some Materials: For materials with very low or very high Poisson’s Ratios, accurate measurement may require specialized equipment.
- Nonlinear Behavior: Lateral strain ratio assumes linear deformation, which may not apply to materials that experience nonlinear stress-strain behavior.
The Future of Poisson’s Ratio in Material Science
- Advanced Composites: As the use of composites increases in industries like aerospace and automotive, understanding lateral strain ratio in complex materials will be key for optimizing performance.
- Nanomaterials: Researchers are exploring the lateral strain ratio of nanomaterials, which may offer new properties that defy traditional material science.
- Smart Materials: In the future, smart materials with tunable Poisson’s Ratios could revolutionize various industries, from construction to medicine.
How Eureka by PatSnap Accelerates Innovation in Poisson’s Ratio Research
What is Eureka by PatSnap?
Eureka by PatSnap is an AI-powered innovation intelligence tool that helps researchers and engineers discover the latest trends in material properties, including lateral strain ratio.
How Eureka Benefits Poisson’s Ratios Research
- Patent Analysis: Eureka helps identify new materials and patents related to lateral strain ratio, allowing researchers to stay ahead of industry developments.
- Competitive Intelligence: The tool tracks innovations in material science, enabling manufacturers to benchmark their products and research against competitors.
- Technology Roadmapping: Eureka provides insights into emerging trends in material science, aiding researchers in setting strategic directions for their work.
Conclusion
Poisson’s Ratio is a key property in material science. It helps us understand how materials react to stress and deformation. This property is crucial in fields like civil engineering, aerospace design, and biomedical applications. Knowing the lateral strain ratio allows engineers to choose the best materials for each task.
FAQs
1️⃣ What is Poisson’s Ratio?
Lateral strain ratio is the ratio of lateral strain to axial strain in a material under stress, indicating how much a material deforms in perpendicular directions when compressed or stretched.
2️⃣ Why is Poisson’s Ratio important in engineering?
Lateral strain ratio helps predict material behavior under stress, which is critical in selecting materials for applications in construction, aerospace, and manufacturing.
3️⃣ How does Poisson’s Ratio affect material selection?
Materials with different Poisson’s Ratios respond differently to stress. For instance, rubber (high lateral strain ratio) is flexible, while concrete (low lateral strain ratio) is stiff and strong.
4️⃣ Can Poisson’s Ratios change with temperature?
Yes, lateral strain ratio can vary with temperature, which is why engineers must account for temperature effects when analyzing material behavior.
5️⃣ How is Poisson’s Ratio measured?
Poisson’s Ratio is typically measured using a tensile test, where axial and lateral strains are measured and the ratio calculated.
To get detailed scientific explanations of Poisson’s Ratio, try Patsnap Eureka.
