Optimization method of discontinuous domain for finite element calculation
An optimization method, a discontinuous technology, applied in design optimization/simulation, calculation, multi-objective optimization, etc., can solve the problems of consumption of computing resources, reduction of algorithm search accuracy, waste of computing resources, etc., to improve search accuracy, algorithm stability, The effect of improving optimization performance
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0047] Below in conjunction with accompanying drawing and specific embodiment the present invention is described in further detail:
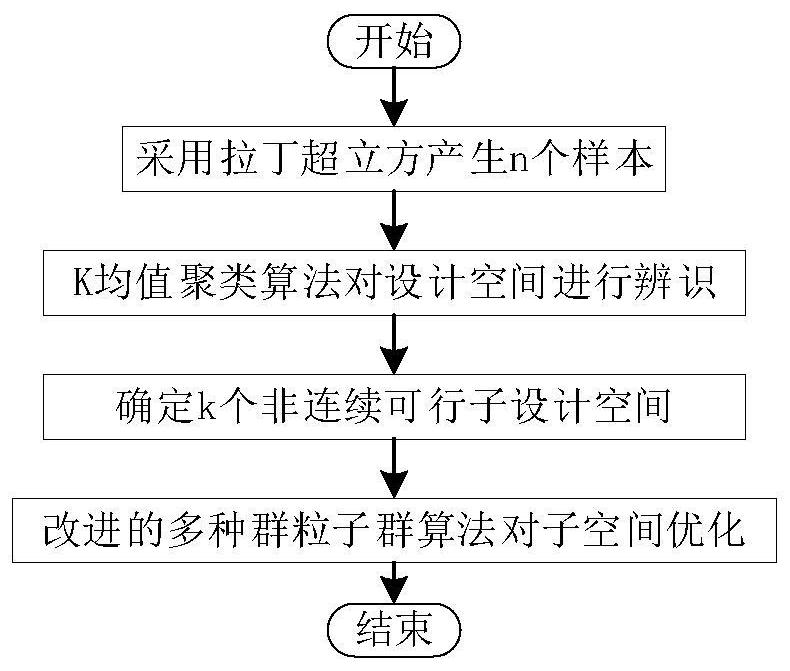
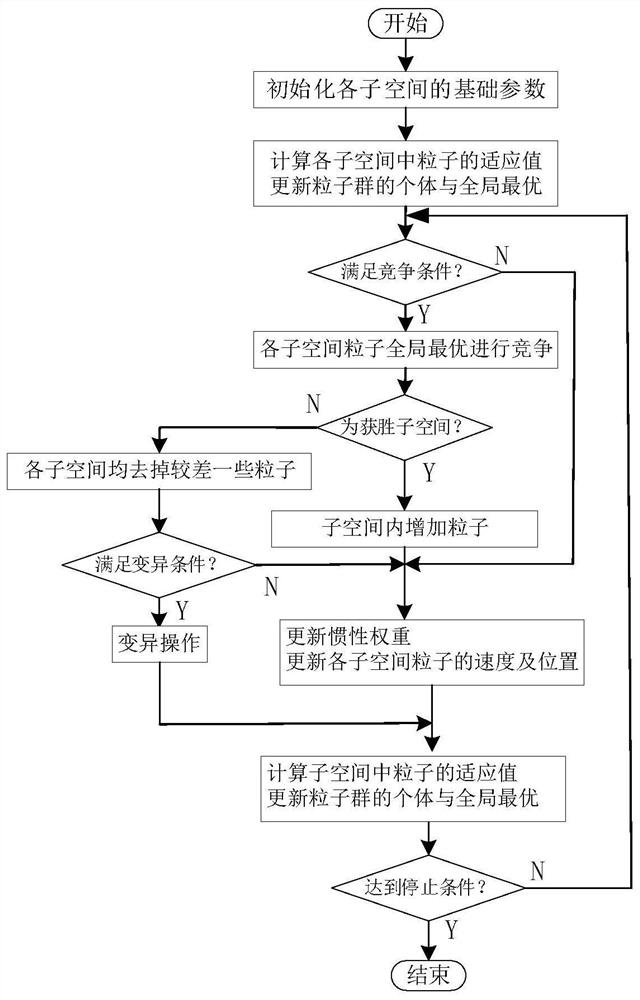
[0048] see figure 1 , the present invention provides an optimization algorithm for discontinuous domains used in finite element calculations. First, the initial design space is identified through Latin hypercube sampling and K-means clustering algorithm, and k discontinuous feasible sub-design spaces are generated for reducing The optimization scope is followed by the optimization of the discontinuous subdesign space using a multi-swarm particle swarm optimization algorithm with competition mechanism.
[0049] Specifically include the following steps:
[0050] Step 1: Generate n samples in the q-dimensional design space through Latin hypercube sampling, calculate the objective function value of each sample and judge whether the constraint conditions are satisfied.
[0051] Step 2: Identify the design space by K-means clustering algorithm. For...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com