Understanding the Chain Rule in Backpropagation

At the heart of modern machine learning, particularly neural networks, lies backpropagation—a crucial algorithm for training models. The chain rule, a fundamental concept from calculus, plays an integral role in this process by facilitating the computation of gradients. To truly appreciate how derivatives flow like pipes and valves, one must understand how the chain rule operates within backpropagation, enabling models to learn efficiently.

The Basics of the Chain Rule

The chain rule is a principle used in calculus to differentiate composite functions. In simple terms, if you have a function z = f(y) where y = g(x), the derivative of z with respect to x is found by multiplying the derivative of z with respect to y and the derivative of y with respect to x. Mathematically, this is expressed as: dz/dx = (dz/dy) * (dy/dx). This concept is crucial in backpropagation because neural networks are essentially compositions of multiple functions.

Backpropagation: The Learning Mechanism

In a neural network, learning involves adjusting weights to minimize the difference between the predicted output and the actual target. To do this, we need to understand how changes in the weights affect the loss function—an error measure. This is where backpropagation, powered by the chain rule, comes into play. By passing the error backward through the network, we can calculate the gradient of the loss with respect to each weight, allowing for precise updates.

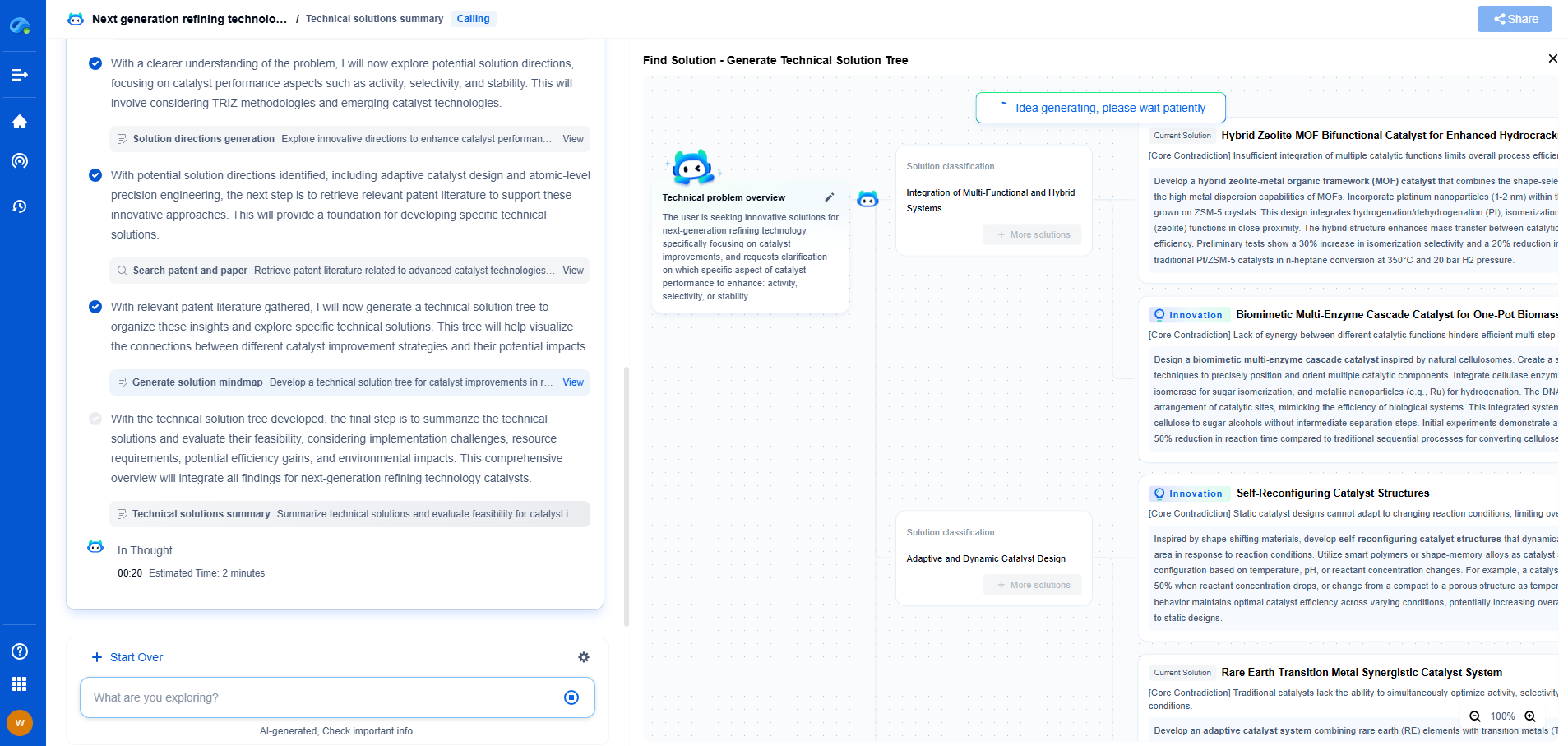
The Flow of Derivatives: Pipes and Valves Analogy

Imagine a complex system of pipes and valves. In this system, water flows through the pipes, and valves control the flow rate. Similarly, in a neural network, information (gradients) flows through the layers (pipes), and the chain rule acts like valves, controlling how these gradients are distributed and combined. Each layer in the network can be thought of as a junction where the chain rule is applied to propagate the derivatives backward.

Calculating Gradients in Layers

When a neural network is trained using backpropagation, the chain rule is applied at each layer to compute the gradient of the loss with respect to the weights. Starting from the output layer, where the loss is directly dependent on the predicted output, the gradient is calculated and then moved backward through each layer. At each step, the chain rule helps compute the local gradients, which are combined to form the global gradient needed to update the weights. This process is akin to adjusting the valves to ensure the correct amount of water flows through each pipe.

Handling Non-linearities

Neural networks are powerful due to their ability to model non-linear relationships, thanks in part to activation functions like the sigmoid, tanh, or ReLU. These functions introduce non-linearities into the network. When backpropagating through these non-linear activation functions, the chain rule is crucial in calculating how the gradients should flow through these non-linear transformations. Each activation function has a specific derivative, which is used in conjunction with the chain rule to update the weights appropriately.

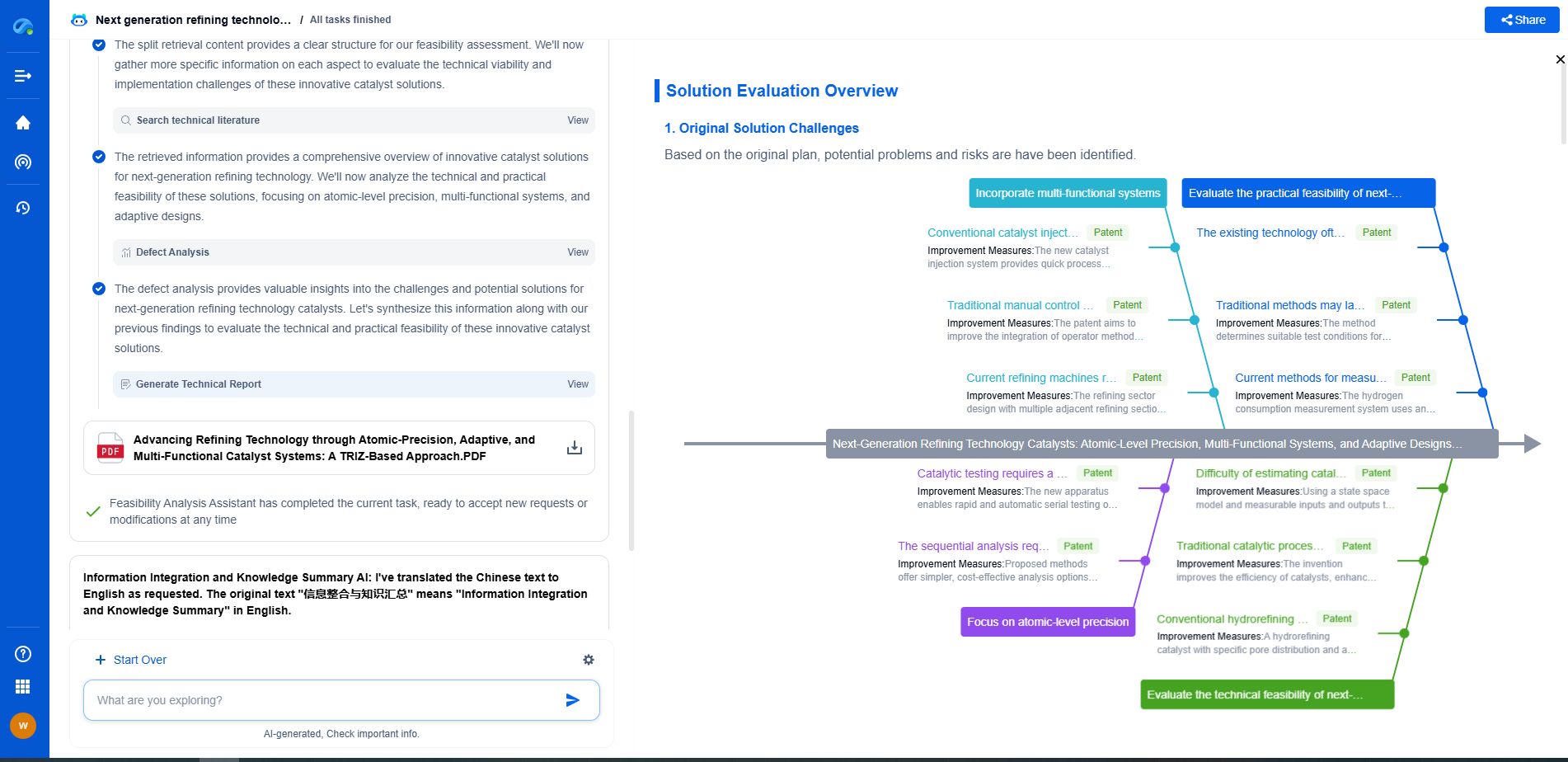
Challenges and Considerations

While the chain rule provides an elegant solution for gradient computation, there are challenges to its application in backpropagation. One such challenge is the vanishing gradient problem, where gradients become exceedingly small as they are propagated backward through deep networks, making weight updates difficult. Various techniques, such as using activation functions like ReLU or employing architectures like Long Short-Term Memory (LSTM) networks, have been developed to mitigate this issue.

Conclusion

The chain rule is an essential component of backpropagation, enabling the gradient computation that underpins the learning process in neural networks. By understanding how derivatives flow like water through pipes and valves, one gains a deeper appreciation of how neural networks learn. This knowledge not only enhances comprehension of the backpropagation algorithm but also equips practitioners to design more effective neural network architectures that can tackle a wide array of complex problems.