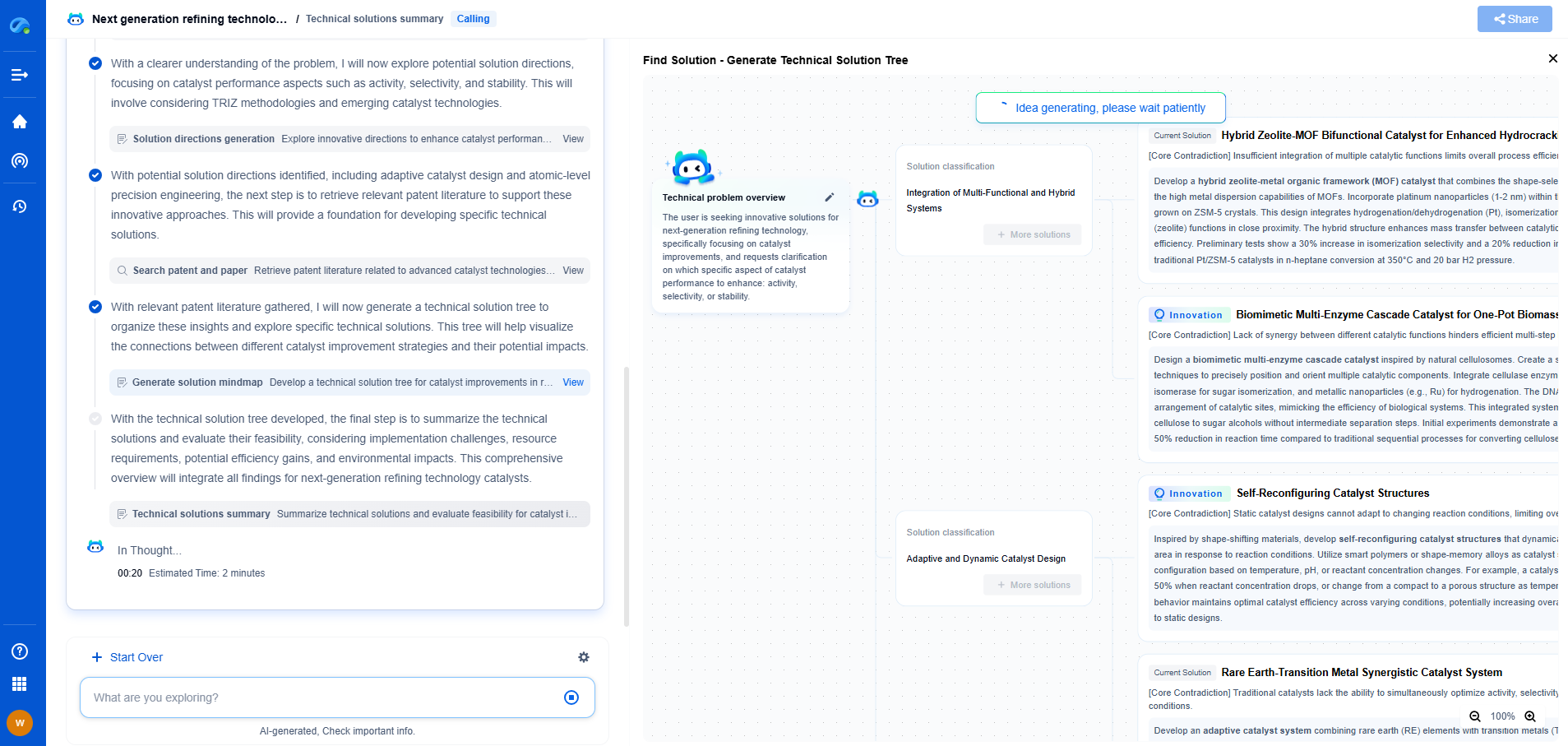
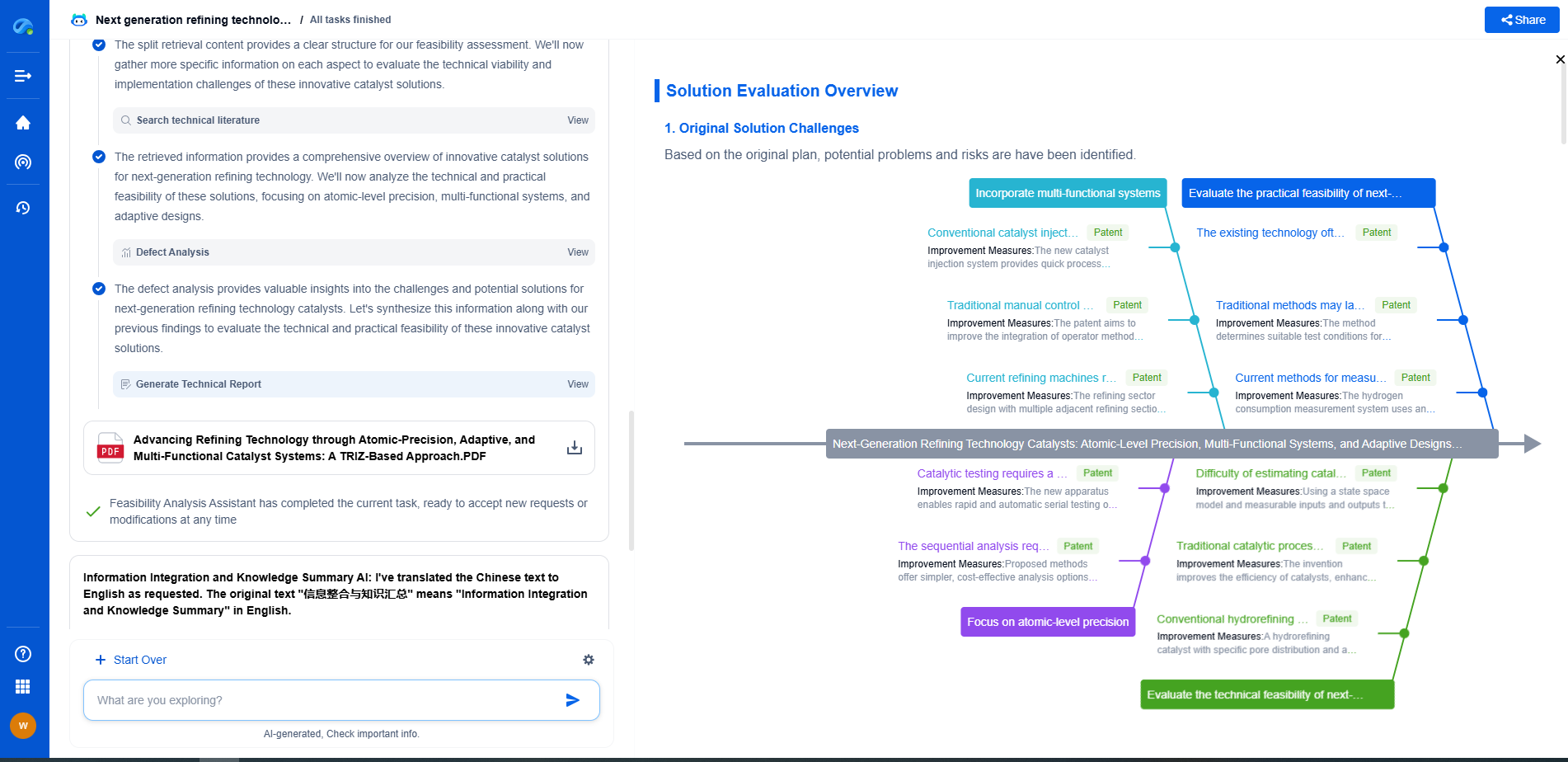
Control gains: What are P, I, and D terms?
JUN 26, 2025 |
Control systems are essential components in various engineering applications, from robotics and aerospace to automotive and industrial automation. At the heart of many control systems is the PID (Proportional-Integral-Derivative) controller, a widely used control loop feedback mechanism. In this article, we will explore what PID controllers are, focusing on the P, I, and D terms, and how they contribute to effective control.
What is a PID Controller?
A PID controller is a control loop mechanism that continuously calculates an error value as the difference between a desired setpoint and a measured process variable. It corrects the error using three separate terms: proportional, integral, and derivative, hence the name PID. Each of these terms has a unique role in the control process, and understanding how they work individually and together is crucial for designing efficient control systems.
The Proportional Term (P)
The proportional term is the most straightforward component of the PID controller. It produces an output that is proportional to the current error value. The proportional gain, denoted as Kp, is a constant that determines the ratio of output response to the error signal. A higher Kp value results in a stronger response to the error, meaning the system will react more aggressively to any deviation from the setpoint.
However, relying solely on the proportional term can lead to steady-state error, where the system fails to reach the desired setpoint because the error is never fully eliminated. Additionally, if the proportional gain is set too high, it can cause the system to become unstable and oscillate.
The Integral Term (I)
The integral term addresses the issue of steady-state error. It integrates the error over time, ensuring that the accumulated error is accounted for in the control output. The integral gain, Ki, determines the contribution of the integral term to the overall control action. By integrating the error, the integral term helps eliminate any residual steady-state error that the proportional term alone cannot resolve.
A properly tuned integral term can improve system accuracy and ensure the setpoint is reached. However, if the integral gain is too high, it can lead to overshoot and instability, as the system can overcompensate for the accumulated error.
The Derivative Term (D)
The derivative term predicts the future behavior of the error by calculating its rate of change. The derivative gain, Kd, influences how much the derivative term will respond to changes in the error. By providing a form of anticipatory action, the derivative term can help dampen system oscillations and improve stability.
The derivative component is particularly useful in systems where rapid changes in error are expected, as it can react quickly to prevent overshoot and improve system settling time. However, excessive derivative action can amplify noise in the system, leading to erratic behavior.
Tuning PID Controllers
Effective control requires proper tuning of the PID gains: Kp, Ki, and Kd. Tuning involves adjusting these gains to achieve the desired system performance, such as stability, speed of response, and minimal overshoot. Various tuning methods exist, ranging from manual trial-and-error to sophisticated algorithms like Ziegler-Nichols and software-based techniques.
The choice of tuning method depends on the specific application and system dynamics. In practice, finding the optimal balance between the P, I, and D terms can be challenging, but it is essential for achieving efficient and reliable control.
Applications of PID Controllers
PID controllers are ubiquitous in engineering and industrial applications due to their simplicity and effectiveness. They are used in temperature control systems, motor speed control, pressure control, and more. The adaptability of PID controllers allows them to be implemented in both simple and complex systems, making them a versatile tool in control engineering.
Conclusion
The P, I, and D terms are fundamental components of PID controllers, each contributing uniquely to system control. By understanding the roles of these terms and how they interact, engineers can design control systems that are both effective and efficient. Proper tuning of the PID gains is essential to achieving optimal performance, ensuring that the controlled process meets its desired outcomes. Whether in simple applications or complex systems, PID controllers continue to play a vital role in modern engineering.
Ready to Redefine Your Robotics R&D Workflow?
Whether you're designing next-generation robotic arms, optimizing manipulator kinematics, or mining patent data for innovation insights, Patsnap Eureka, our cutting-edge AI assistant, is built for R&D and IP professionals in high-tech industries, is built to accelerate every step of your journey.
No more getting buried in thousands of documents or wasting time on repetitive technical analysis. Our AI Agent helps R&D and IP teams in high-tech enterprises save hundreds of hours, reduce risk of oversight, and move from concept to prototype faster than ever before.
👉 Experience how AI can revolutionize your robotics innovation cycle. Explore Patsnap Eureka today and see the difference.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com