Understanding Gradient Descent and Stochastic Gradient Descent

Gradient Descent Overview

Gradient Descent is a fundamental optimization technique widely used in machine learning and deep learning to minimize a function by iteratively moving towards the minimum value of a loss function. This function generally measures how well a particular model performs given its parameters. It's essential for training algorithms like linear regression, logistic regression, and neural networks.

The key idea behind gradient descent is to use the gradient (i.e., the derivative) of the loss function to determine the direction in which the function decreases most rapidly. By taking steps proportional to the negative of the gradient, gradient descent moves the parameters in the direction that reduces the loss.

How Gradient Descent Works

In gradient descent, we start with an initial set of parameters and iteratively update them. For each iteration, the algorithm computes the gradient of the loss function with respect to the parameters. It then updates the parameters in the opposite direction of the gradient by a factor proportional to a learning rate. The learning rate is a hyperparameter that determines the size of the steps taken during each update. If the learning rate is too small, convergence can be slow, while a large learning rate might cause the algorithm to overshoot the minimum.

The algorithm stops when the change in the loss function is smaller than a predefined threshold or after a set number of iterations.

Limitations of Gradient Descent

While effective, gradient descent has limitations. It requires the computation of the gradient of the entire dataset to update parameters, which can be computationally expensive and time-consuming, especially for large datasets. Additionally, gradient descent can get stuck in local minima, though this issue is often mitigated in practice by using techniques like momentum or advanced algorithms like Adam.

Introduction to Stochastic Gradient Descent

Stochastic Gradient Descent (SGD) is a variant of gradient descent that addresses some of the limitations of the traditional method. Instead of using the entire dataset to compute the gradient, SGD updates the model parameters using only a single data point or a mini-batch of data points at each iteration.

Advantages of Stochastic Gradient Descent

The main advantage of SGD is its efficiency. By using only a subset of the data, it significantly reduces the computation time per iteration. This makes it particularly useful for large datasets and online learning scenarios where data comes in streams or batches.

SGD also introduces more noise into the optimization process, which can help the algorithm escape local minima and potentially find a better global minimum. The noise allows the algorithm to explore the parameter space more thoroughly, which can be beneficial for non-convex functions typical in deep learning.

Challenges with Stochastic Gradient Descent

Despite its efficiency, SGD introduces challenges. The noise, while helpful in escaping local minima, can also lead to erratic updates, making convergence more difficult and requiring more iterations to stabilize. The choice of learning rate becomes crucial for the performance of SGD. Too high a learning rate may cause the algorithm to diverge, while too low a value may slow down convergence.

To mitigate these issues, practitioners often use techniques such as learning rate schedules, momentum, or adaptive learning rate algorithms like RMSprop or Adam, which help stabilize the training process and accelerate convergence.

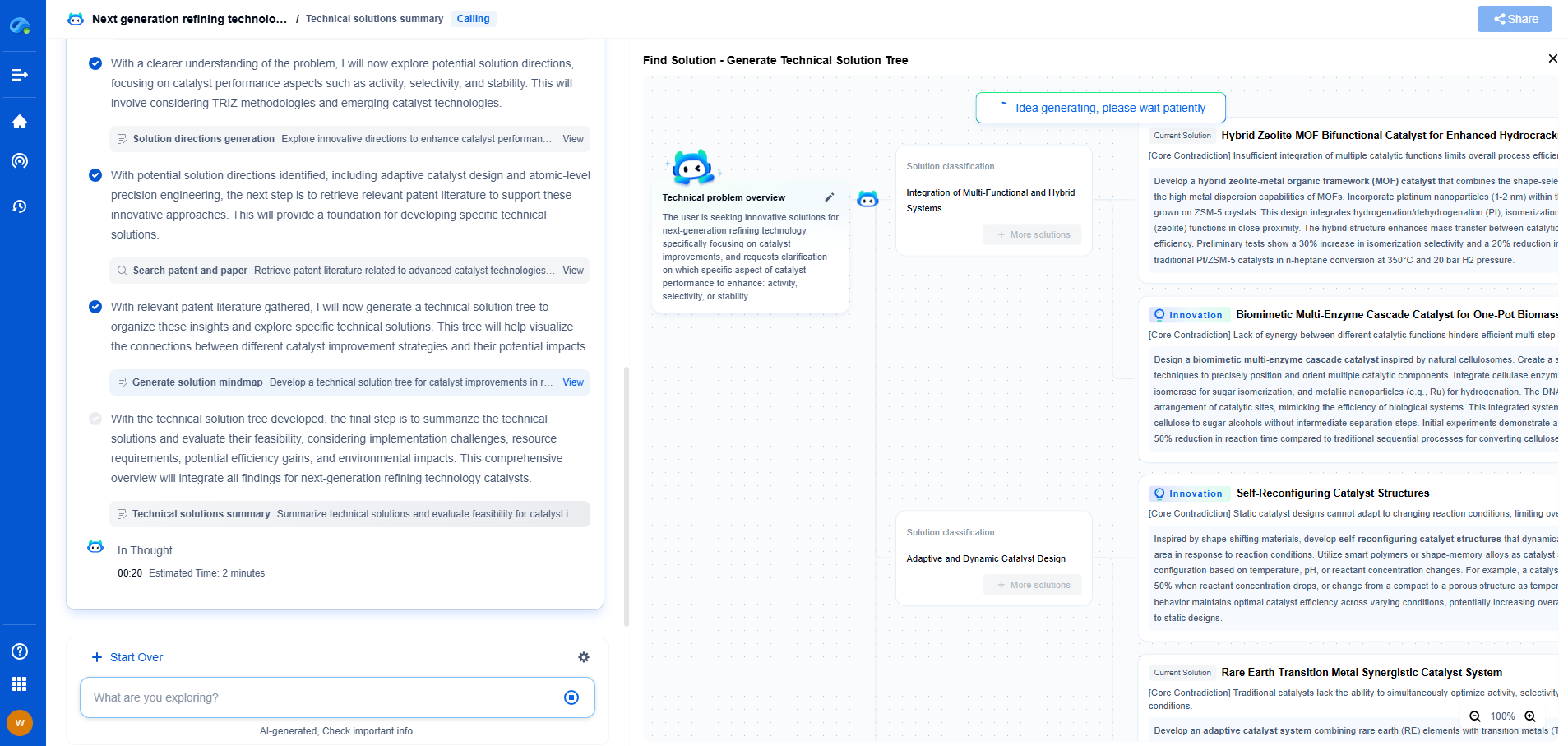
Key Differences Between Gradient Descent and Stochastic Gradient Descent

The primary difference between gradient descent and stochastic gradient descent lies in the amount of data used to compute the gradient during each iteration. Gradient descent utilizes the entire dataset, while SGD uses a single data point or mini-batch, making it more efficient and suitable for large-scale and online learning.

Additionally, the convergence behavior differs between the two. Gradient descent has smoother convergence since it uses the complete dataset, while SGD has more fluctuation due to its stochastic nature.

Conclusion

Both gradient descent and stochastic gradient descent are powerful tools in the optimization landscape of machine learning. The choice between them largely depends on the size of the dataset and the specific requirements of the task at hand. For smaller, manageable datasets, traditional gradient descent is often sufficient. However, for larger datasets or online learning scenarios, stochastic gradient descent offers a more feasible and efficient alternative. Understanding the strengths and limitations of each method is crucial for effectively applying them to real-world machine learning problems.