Exploring various loss functions is crucial for understanding how deep learning models are trained. The loss function measures the difference between the predicted output of the model and the actual target value. By minimizing this difference, models learn to make more accurate predictions. Below, we discuss several commonly used loss functions in deep learning, each suited for different types of tasks.

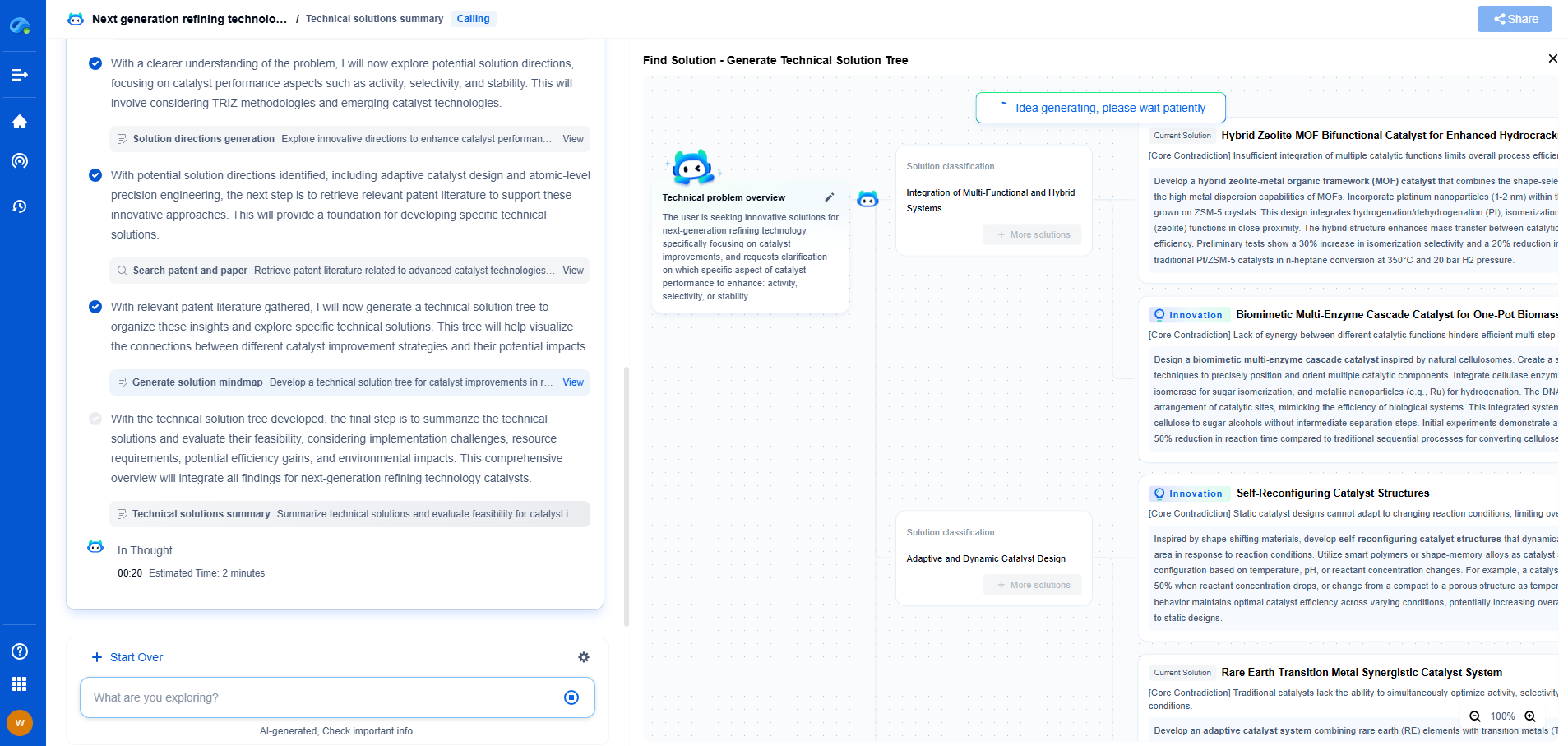
Understanding Loss Functions

Loss functions are at the heart of the learning process in deep neural networks. They quantify how well the model performs and guide the optimization process. A good choice of loss function can significantly improve model performance, while an inappropriate one can lead to poor results. The selection often depends on the nature of the task, such as regression, classification, or more complex objectives like ranking or segmentation.

Mean Squared Error (MSE)

Mean Squared Error is one of the most straightforward and commonly used loss functions for regression tasks. It calculates the square of the difference between each predicted value and the actual target value, then averages those squared differences. The formula for MSE is:

MSE = (1/n) * Σ(actual - predicted)²

This loss function is sensitive to outliers, as large errors have a disproportionately large effect on the MSE due to squaring. It is best suited for tasks where errors need to be punished severely.

Mean Absolute Error (MAE)

Mean Absolute Error is another loss function used for regression tasks, similar to MSE but with a fundamental difference: it calculates the absolute difference between predicted and actual values. The formula is:

MAE = (1/n) * Σ|actual - predicted|

MAE is more robust to outliers than MSE because it doesn’t involve squaring the errors, making it a preferable choice when handling data with many outliers.

Cross-Entropy Loss

Cross-Entropy Loss, also known as log loss, is widely used for classification problems. It measures the performance of a classification model whose output is a probability value between 0 and 1. The formula for binary classification is:

Cross-Entropy = - (y * log(p) + (1-y) * log(1-p))

For multi-class classification, the loss is calculated as the sum of the categorical cross-entropy for each class. This loss function is very effective for training models where each class is mutually exclusive.

Hinge Loss

Hinge Loss is specifically used for "maximum-margin" classification, most notably with support vector machines. For binary classification, the hinge loss function is:

Hinge Loss = max(0, 1 - y * f(x))

Here, y is the actual label, and f(x) is the predicted label. This loss function ensures that the model not only classifies correctly but also does so with a certain margin.

Kullback-Leibler Divergence (KL Divergence)

KL Divergence is a measure used for distribution learning problems. It measures how one probability distribution diverges from a second, expected probability distribution. In practice, it is used in tasks like variational autoencoders where one needs to compare the similarity between two distributions.

KL(p || q) = Σ p(x) log(p(x) / q(x))

This function is particularly useful in scenarios involving probabilistic models and is often used in natural language processing and other tasks that model data distributions.

Huber Loss

Huber Loss is an interesting combination of MSE and MAE, providing a balance between the two. It is less sensitive to outliers in data than the squared error loss. The formula is piecewise:

Huber Loss = { 0.5 * (actual - predicted)², if |actual - predicted| ≤ δ
δ * (|actual - predicted| - 0.5 * δ), otherwise }

This makes Huber Loss particularly effective for regression tasks where the data might contain outliers, but those should not dominate the learning process.

Conclusion

Selecting the appropriate loss function is a critical step in the model development process. It aligns the optimization process with the specific needs and characteristics of the task at hand. By understanding the strengths and weaknesses of each loss function, practitioners can tailor their models to achieve optimal performance in various applications. Whether dealing with regression, classification, or more complex modeling tasks, the right loss function can make a significant difference in the success of your deep learning project.