Understanding FFT Optimization Techniques

The Fast Fourier Transform (FFT) is a cornerstone of digital signal processing, enabling efficient computation of the discrete Fourier transform (DFT) and its inverse. Originally introduced by Cooley and Tukey in 1965, the FFT has since undergone numerous enhancements and variations to improve performance across different applications and architectures. This blog explores some of the crucial optimization techniques for FFT, from the well-known Radix-2 algorithm to more sophisticated approaches like Prime Factor Algorithms.

Radix-2 FFT: The Foundation

The Radix-2 FFT is commonly used due to its simplicity and efficiency when the input size, N, is a power of two. This divide-and-conquer algorithm recursively splits the DFT into smaller DFTs, reducing the computational complexity from O(N^2) to O(N log N). The basic idea is to decompose the computation into two smaller FFTs of size N/2, exploiting the periodicity and symmetry properties of the DFT.

While Radix-2 is optimal for powers of two, it is less efficient for other input sizes. However, its influence extends to numerous advancements and variations in the FFT domain.

Radix-4 and Higher Radix Variants

To further enhance computational efficiency, Radix-4 and higher radix FFTs were developed. These variants reduce the number of arithmetic operations by breaking down the problem into even larger chunks at each stage. For instance, Radix-4 processes four elements at a time, effectively halving the number of stages required compared to Radix-2. This results in fewer multiplicative operations, which are typically more computationally expensive than additions.

Higher radix algorithms like Radix-8 or mixed-radix approaches offer similar benefits but often require more intricate handling of data permutations and twiddle factors. Such algorithms are well-suited for vectorized implementations and are often used in scenarios where the input size is not a perfect power of two.

Split-Radix FFT: Combining the Best of Both Worlds

The Split-Radix FFT algorithm is an ingenious technique that combines the strengths of both Radix-2 and Radix-4 approaches. By cleverly splitting the FFT into a combination of Radix-2 and Radix-4 computations at each recursive step, Split-Radix manages to reduce the number of operations further, making it one of the most efficient FFT algorithms available for certain input sizes.

Despite its computational efficiency, the Split-Radix FFT can be more complex to implement and optimize, especially on modern hardware architectures. However, its performance benefits often justify the additional complexity in high-performance computing applications.

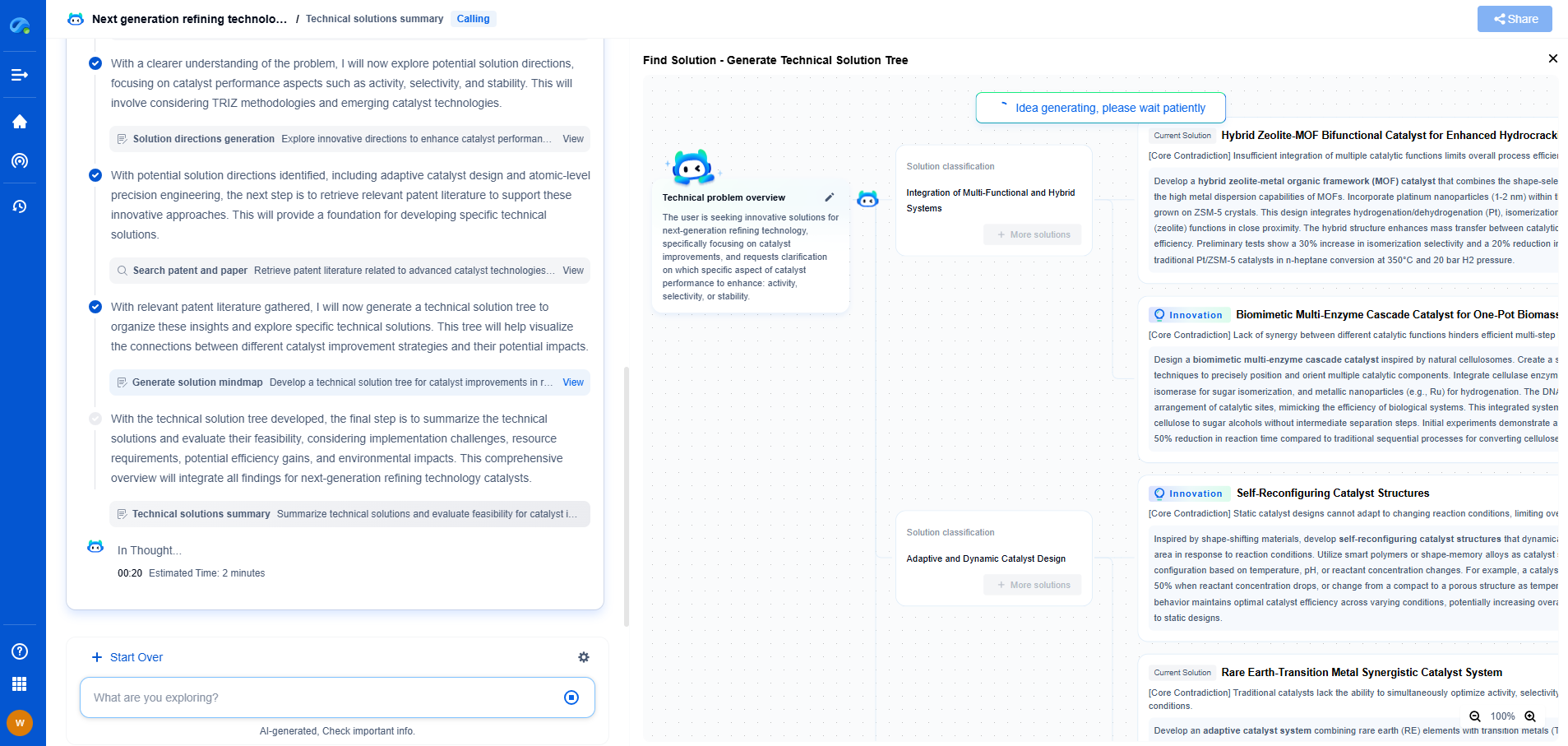
Prime Factor FFT: Handling Any Size with Elegance

When dealing with input sizes that are not highly composite or are large primes, the Prime Factor Algorithm (PFA) becomes invaluable. PFA leverages the Chinese Remainder Theorem to decompose the FFT problem into smaller, independent subproblems, which can then be solved using any efficient algorithm, such as Radix-2 or Radix-4.

One of the key advantages of PFA is its ability to handle arbitrary input sizes without requiring zero-padding, which can be inefficient. This makes it particularly attractive for applications like real-time signal processing, where every sample counts.

Implementing FFT on Modern Architectures

With the advent of modern computing architectures, optimizing FFT implementations for specific hardware components has become crucial. Techniques such as loop unrolling, vectorization, and parallel processing are essential for fully exploiting the capabilities of CPUs, GPUs, and specialized hardware like FPGAs.

Moreover, memory access patterns play a significant role in FFT performance, especially on systems with complex memory hierarchies. Techniques like cache blocking and prefetching are often employed to ensure efficient memory usage and reduce latency.

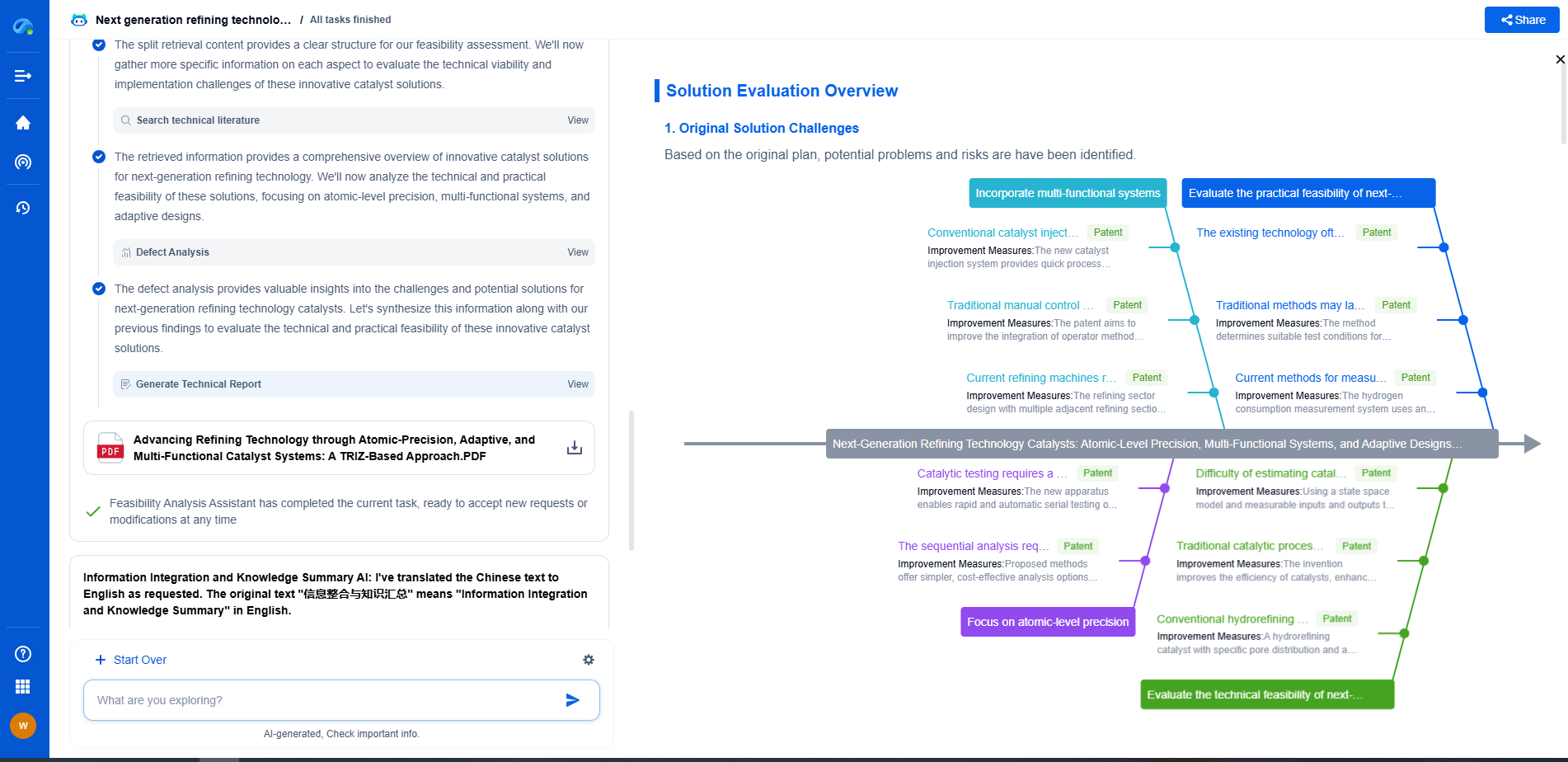
Conclusion: The Path Forward for FFT Optimization

FFT optimization is an ongoing journey, with researchers continually seeking new ways to enhance performance and adapt to emerging technologies. From the classic Radix-2 algorithm to advanced Prime Factor and hybrid techniques, each method offers unique advantages tailored to specific scenarios and constraints.

As hardware continues to evolve, so too will the techniques for optimizing FFT, ensuring its place as an indispensable tool in the arsenal of digital signal processing. For anyone keen on diving deeper into this field, understanding these optimization techniques is not only beneficial but essential for pushing the boundaries of what is possible with FFT.