Understanding the Fast Fourier Transform (FFT) and Short-Time Fourier Transform (STFT) is essential for those working in fields involving signal processing, such as audio engineering, telecommunications, and even finance. Both methods are used to convert signals from the time domain to the frequency domain, but they each have their unique strengths and weaknesses. In this blog, we explore the trade-offs between frequency resolution and time localization in FFT and STFT, helping you choose the right tool for your specific needs.

Understanding FFT

The Fast Fourier Transform is an efficient algorithm to compute the Discrete Fourier Transform (DFT) and its inverse. The DFT itself is a mathematical technique used to transform discrete signals from the time domain into the frequency domain. The crux of FFT's appeal is its ability to handle large datasets quickly, due to its computational efficiency.

When it comes to frequency resolution, FFT shines. It provides a high-resolution spectrum, allowing us to distinguish between closely spaced frequency components. This makes FFT particularly useful in applications where frequency accuracy is paramount, such as spectral analysis of stationary signals or signals where the frequency content does not change over time.

However, FFT has a significant limitation: it assumes that the entire signal is stationary. This means that all the frequencies present in the signal remain constant over the duration of the signal being analyzed. In practice, many real-world signals are non-stationary, meaning their frequency content changes over time. This assumption results in a lack of time localization, making FFT less effective for analyzing transient signals or signals with time-varying frequencies.

Introduction to STFT

The Short-Time Fourier Transform was developed to address the limitations of FFT concerning time-varying signals. STFT involves dividing the signal into smaller segments or "windows," each of which is analyzed separately using FFT. This windowing process allows STFT to provide time-localized frequency information, offering a balance between time and frequency resolution.

The key parameter in STFT is the window size. A smaller window provides better time localization but at the cost of frequency resolution. Conversely, a larger window offers better frequency resolution but poorer time localization. Therefore, selecting an appropriate window size is crucial, as it directly impacts the trade-off between temporal and spectral resolution.

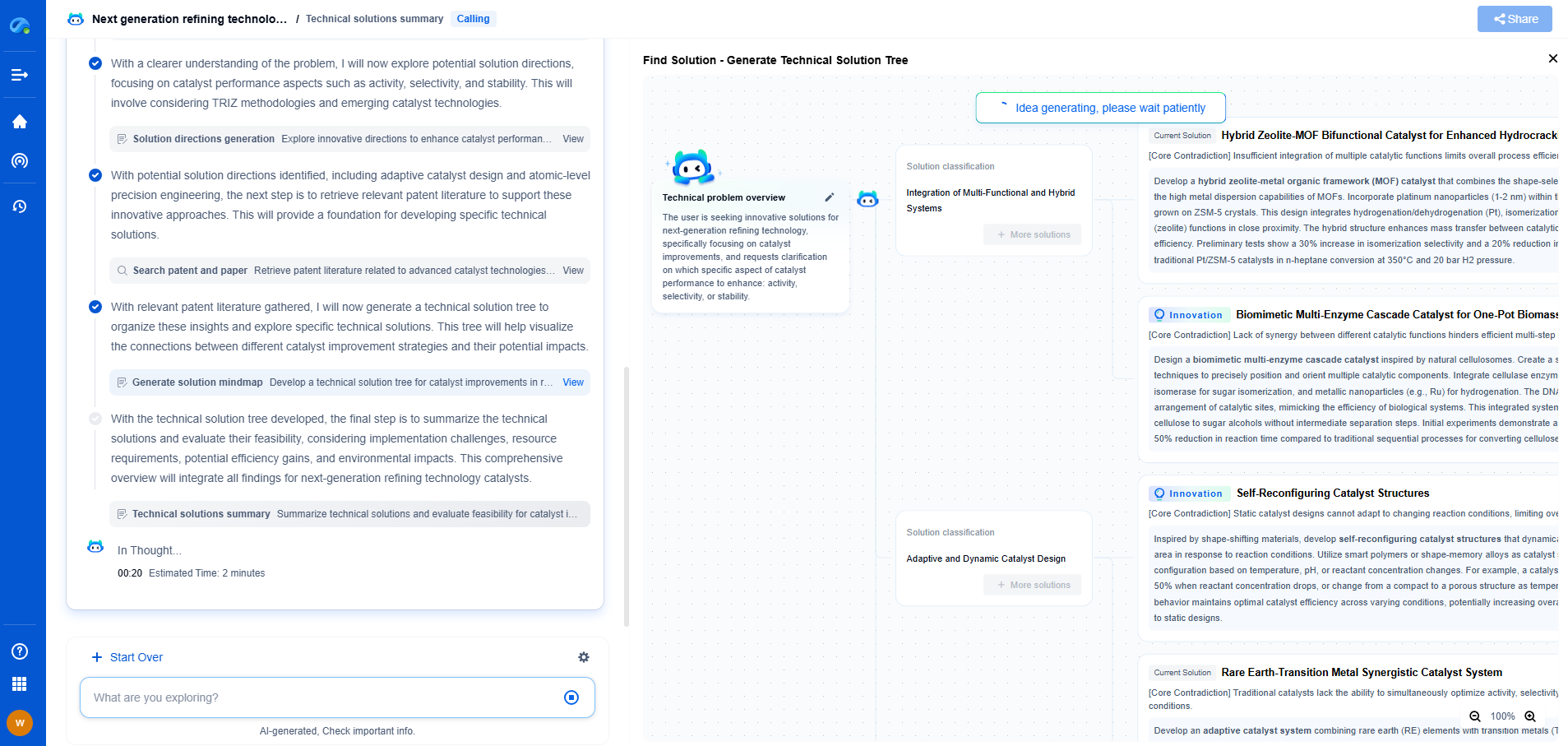
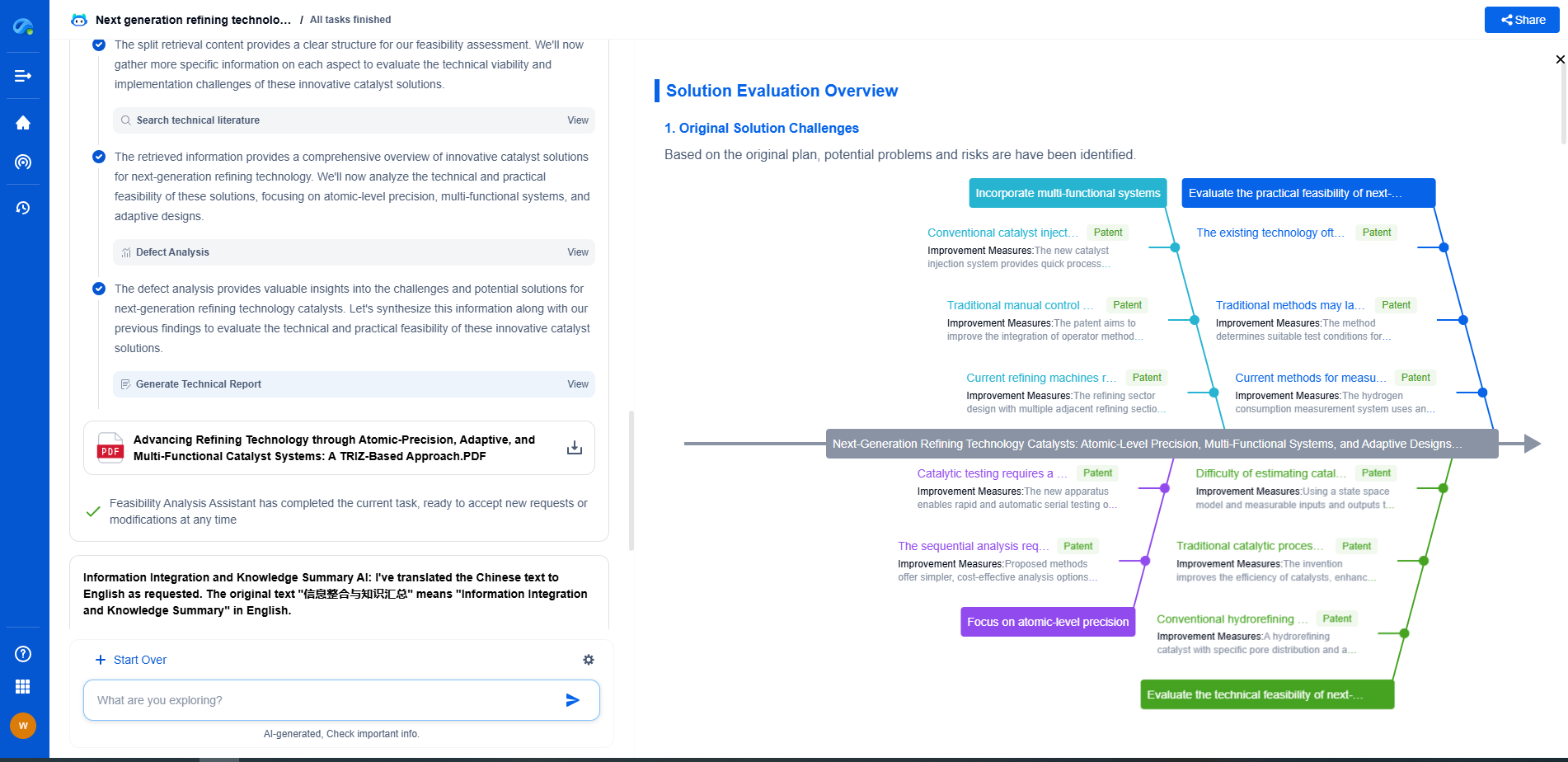
Trade-offs Between Frequency Resolution and Time Localization

When comparing FFT and STFT, it's important to understand the inherent trade-offs between frequency resolution and time localization. These trade-offs are primarily dictated by the nature of the signal being analyzed and the specific requirements of the application.

For signals that are stationary or have minimal frequency variation over time, FFT is typically the preferred choice. Its ability to provide high-frequency resolution ensures that even closely spaced frequency components are accurately identified. However, if the signal is non-stationary and requires time-localized frequency analysis, STFT becomes more suitable.

Choosing the right window size in STFT is an art as much as it is a science. A smaller window size ensures better detection of transient signals, capturing rapid changes in frequency content. On the other hand, a larger window size provides more accurate frequency resolution, which is essential for signals with stable frequency components. The choice of window size, therefore, depends on the specific application and the nature of the signal being analyzed.

Applications and Practical Considerations

In practice, the choice between FFT and STFT often depends on the specific requirements of the application. For instance, in audio processing, where signals may have rapidly changing frequency content, STFT is often preferred due to its ability to capture time-localized frequency information. In contrast, for applications such as power spectrum analysis or vibration analysis in mechanical systems, where signals are relatively stationary, FFT's high-frequency resolution is advantageous.

It's also important to consider computational resources. While FFT is computationally efficient, STFT requires multiple FFTs, one for each window, which can be computationally intensive. This is an important consideration when working with large datasets or in real-time applications where processing speed is critical.

Conclusion

Understanding the trade-offs between FFT and STFT is essential for effective signal analysis. While FFT provides superior frequency resolution for stationary signals, STFT offers a valuable compromise between frequency and time resolution, making it suitable for analyzing non-stationary signals. By carefully considering the nature of the signal and the specific requirements of your application, you can choose the right tool to achieve the best results. Whether you're analyzing audio signals, financial data, or any other type of time-varying signal, mastering the use of FFT and STFT will enhance your ability to extract meaningful insights from your data.