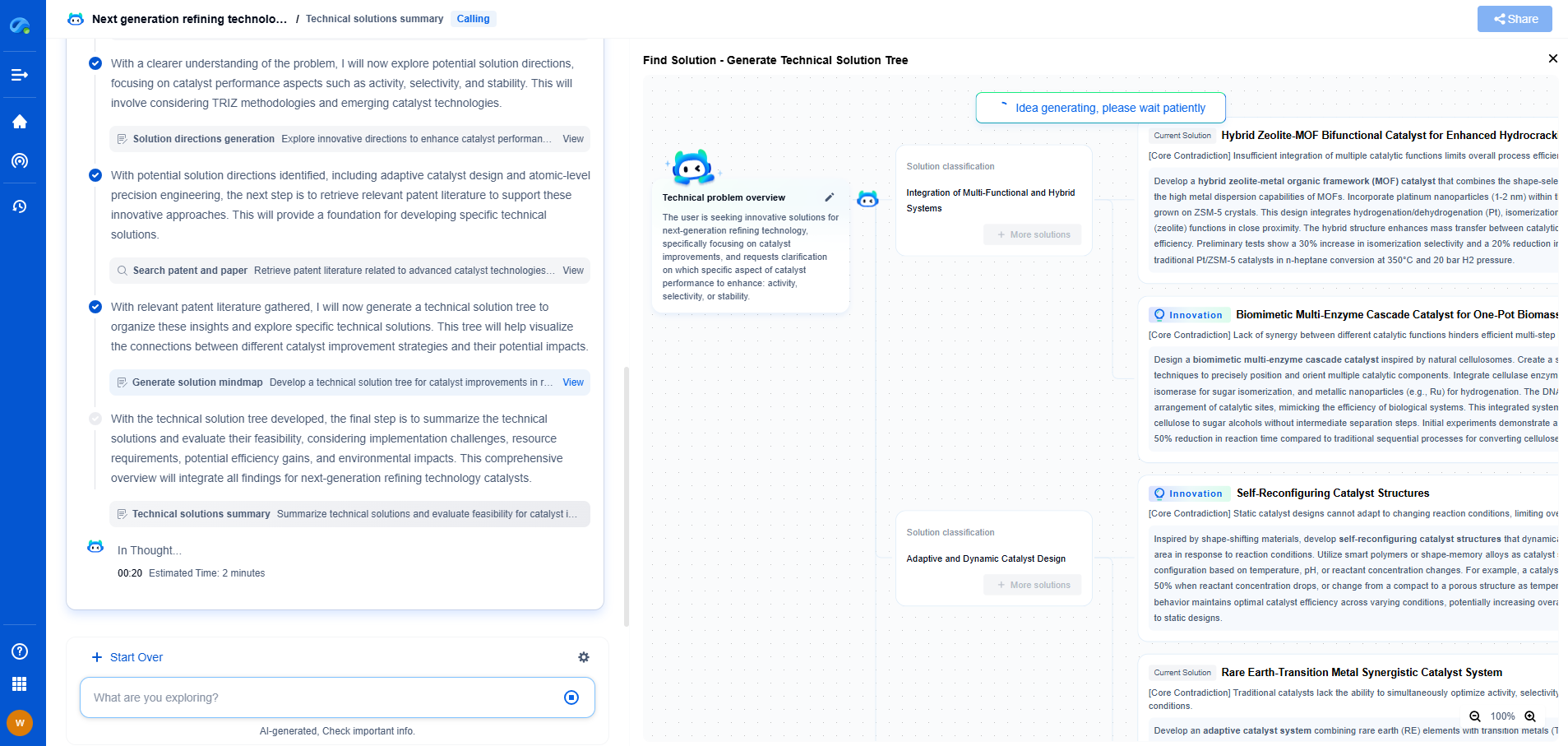
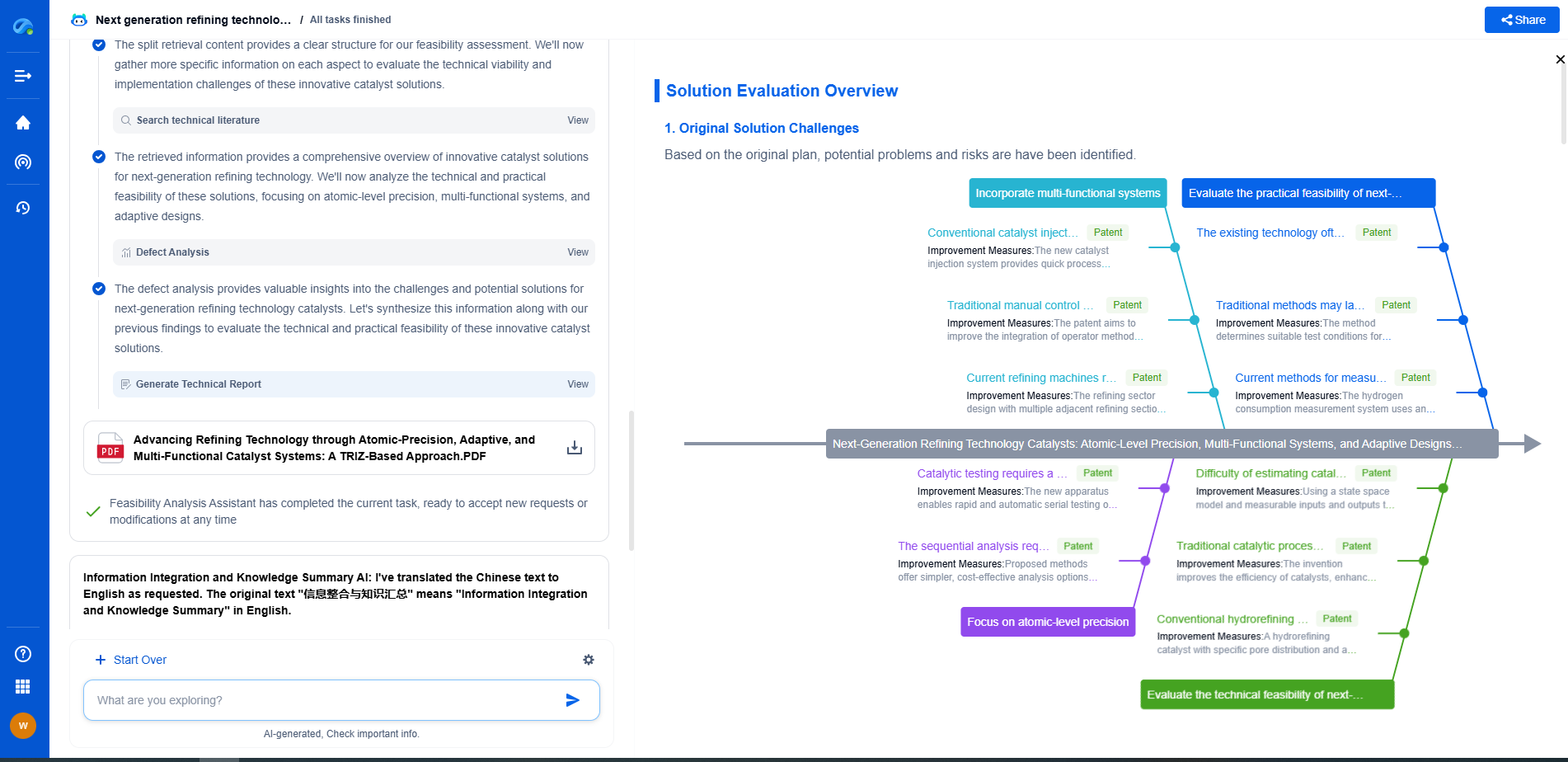
FIR vs. IIR Filters: Computational Efficiency vs. Phase Linearity
JUL 17, 2025 |
In the realm of digital signal processing, filters play a pivotal role in refining and manipulating signals. Two primary types of digital filters are Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters. Each comes with its own set of advantages and challenges, particularly concerning computational efficiency and phase linearity. This article delves into the nuances of FIR and IIR filters, exploring how they differ in these crucial areas.
Understanding FIR and IIR Filters
FIR filters are characterized by a finite duration of their impulse response, meaning that they settle to zero in a finite amount of time. This is due to their inherent design, which relies on a sum of a finite number of delayed signal samples. This simplicity in structure makes FIR filters inherently stable and easy to design.
On the other hand, IIR filters have an impulse response that theoretically lasts indefinitely. They achieve this through feedback mechanisms, which allow them to use both the current and past input values and the past output values. This feedback can lead to higher computational efficiency, as they often require fewer coefficients to achieve a specific filter response compared to FIR filters.
Computational Efficiency
One of the main considerations when choosing between FIR and IIR filters is computational efficiency. IIR filters generally require fewer arithmetic operations—such as multiplications and additions—for a given filter specification. This efficiency stems from their ability to achieve sharp frequency responses with fewer coefficients due to their recursive nature.
In applications where computational resources are limited, such as in embedded systems or real-time processing scenarios, the lower computational load of IIR filters can be a significant advantage. This efficiency often translates to faster processing speeds and reduced power consumption, crucial factors in battery-powered or resource-constrained devices.
Phase Linearity
Despite their computational efficiency, IIR filters have a notable downside: they typically do not provide linear phase responses. A linear phase response is crucial in applications where phase distortion can affect signal integrity, such as in audio processing or communications systems. Non-linear phase responses can lead to phase distortion, which can alter the shape of the signal waveform, introducing unwanted artifacts.
FIR filters, in contrast, can be designed to have an exactly linear phase response. This means that all frequency components of the input signal are delayed by the same amount, preserving the waveform shape of signals. This property makes FIR filters particularly valuable in applications where phase linearity and signal fidelity are paramount.
Trade-offs and Applications
The choice between FIR and IIR filters often boils down to a trade-off between computational efficiency and phase linearity. In applications where phase accuracy is more critical than computational load, such as in audio processing or certain communication systems, FIR filters are usually preferred despite their higher computational demands.
Conversely, in scenarios where computational resources are limited, or where sharp filter responses are needed with minimal computational cost, IIR filters become the go-to option. Examples include control systems and real-time processing applications, where the fast response and stability of IIR filters are advantageous.
Design Considerations
When designing filters, engineers must consider several factors, such as the desired filter characteristics, the available computational resources, and the acceptable level of phase distortion. Tools like MATLAB and Python's SciPy library provide robust environments for simulating and designing both FIR and IIR filters, allowing engineers to model different filter responses and analyze their performance with respect to the application needs.
Conclusion
The debate between FIR and IIR filters is not about which is superior overall, but rather which is more suitable for a specific application. FIR filters offer the advantage of phase linearity but at the cost of higher computational demand. IIR filters, while computationally efficient, may introduce phase distortion. Understanding these trade-offs is essential for engineers and designers to make informed decisions that best meet the requirements of their projects. Ultimately, the choice is guided by the specific needs of the application, balancing the trade-offs between computational efficiency and phase linearity.
Whether you’re developing multifunctional DAQ platforms, programmable calibration benches, or integrated sensor measurement suites, the ability to track emerging patents, understand competitor strategies, and uncover untapped technology spaces is critical.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
🧪 Let Eureka be your digital research assistant—streamlining your technical search across disciplines and giving you the clarity to lead confidently. Experience it today.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com