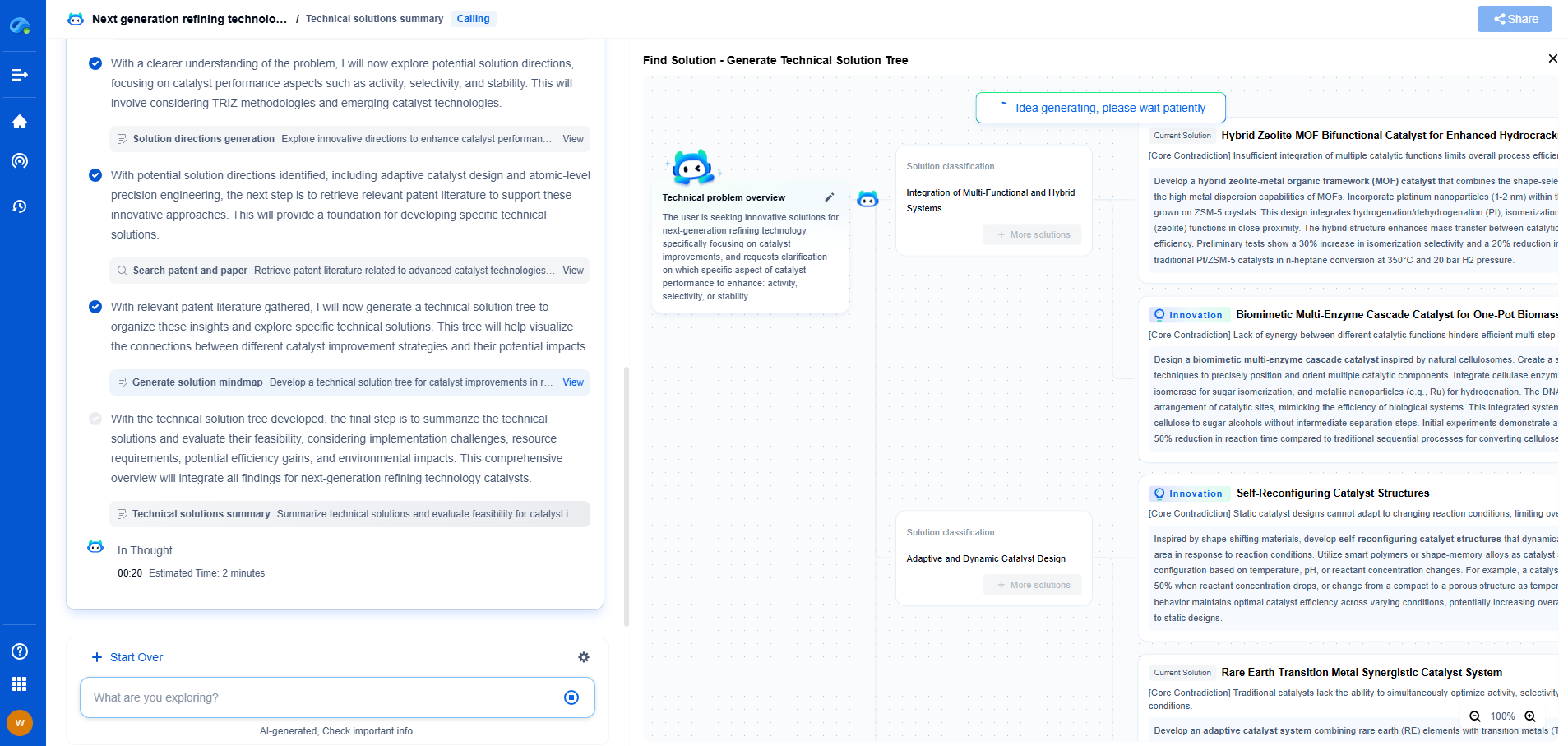
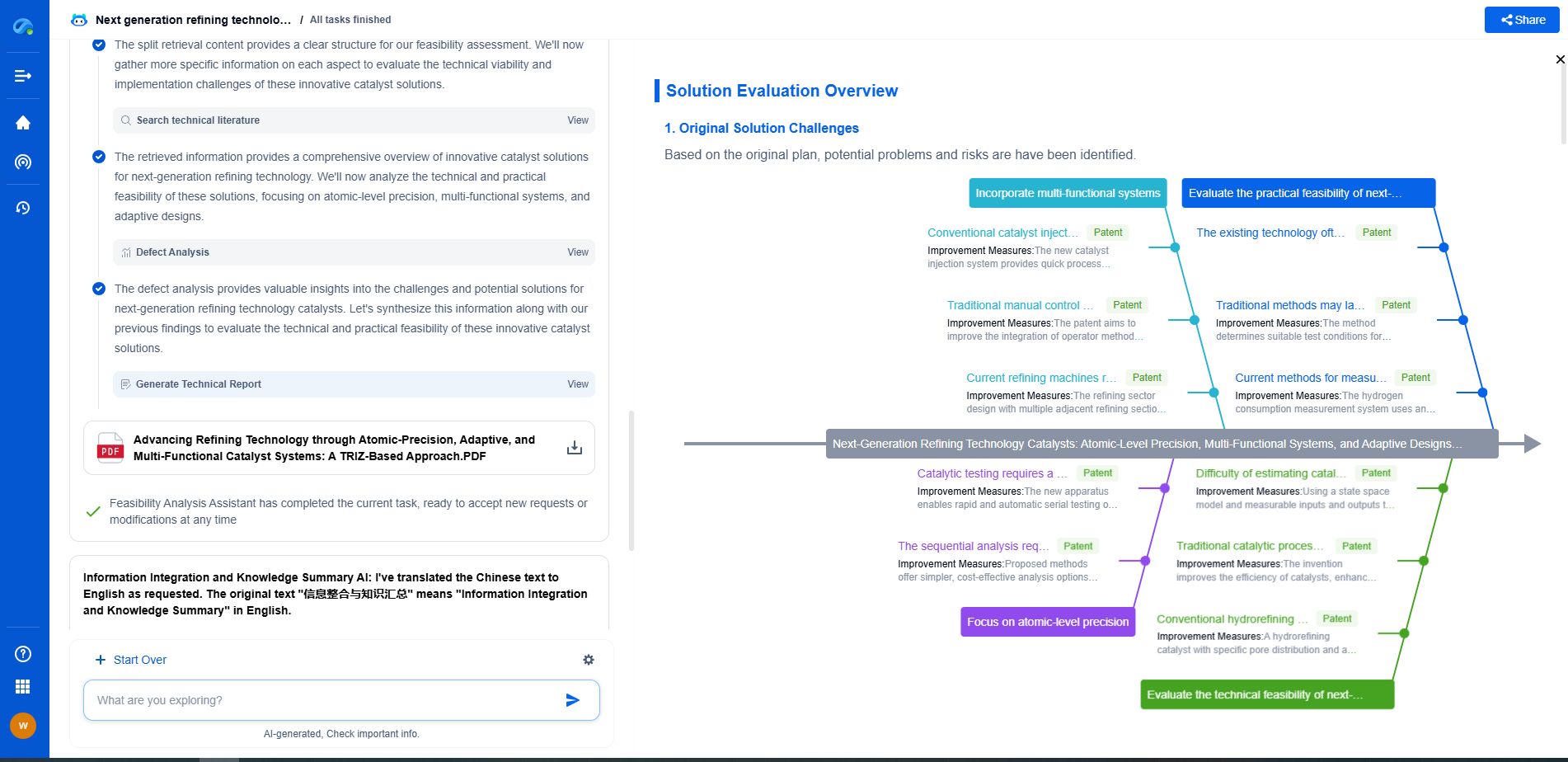
How Does Bayesian Updating Work in Machine Learning?
JUN 26, 2025 |
Bayesian updating is a powerful statistical method that plays a crucial role in machine learning by providing a framework for updating predictions or models as new data becomes available. The method is rooted in Bayes' Theorem, which provides a mathematical way to update the probability of a hypothesis based on new evidence. In the realm of machine learning, Bayesian updating is utilized to refine models, making them more accurate and reliable over time.
The Basics of Bayes' Theorem
To understand Bayesian updating, it's essential to grasp the basics of Bayes' Theorem. Named after Reverend Thomas Bayes, this theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event. Mathematically, Bayes' Theorem is expressed as:
P(H|E) = [P(E|H) * P(H)] / P(E)
Where:
- P(H|E) is the posterior probability of hypothesis H given the evidence E.
- P(E|H) is the likelihood of observing evidence E given that H is true.
- P(H) is the prior probability of the hypothesis before considering the evidence.
- P(E) is the total probability of the evidence.
Bayesian Updating in Machine Learning
Machine learning models often start with initial assumptions or prior distributions about the data, known as priors. As the model encounters more data, it uses Bayesian updating to refine these assumptions, resulting in posterior distributions that better reflect the reality of the data. Here's how this process unfolds in a typical machine learning scenario:
1. Initial Model: At the beginning, a model is built using prior data or assumptions. This initial model represents what is already known or believed about the data.
2. Collecting Data: As new data becomes available, it is used as evidence in the Bayesian updating process. This data provides additional information that can help improve the model.
3. Likelihood Function: The likelihood function assesses how well the new data supports the current model. It calculates the probability of observing the new data given the parameters of the current model.
4. Updating the Model: Using Bayes' Theorem, the model is updated to reflect the new data. This involves combining the prior distribution with the likelihood to generate a posterior distribution, which provides updated probabilities for the model’s parameters.
5. Iteration: This process is repeated as more data is collected, allowing the model to continually improve and become more accurate over time.
Applications of Bayesian Updating in Machine Learning
Bayesian updating is widely employed in various machine learning applications. Some of the most prominent applications include:
1. Natural Language Processing (NLP): Bayesian updating is used to improve language models, refining predictions about word sequences as more text data is analyzed.
2. Robotics: In robotic systems, Bayesian updating helps in real-time decision-making by continuously integrating sensor information to update the robot's understanding of its environment.
3. Computer Vision: In object detection and recognition tasks, Bayesian methods update model predictions based on new visual data, enhancing accuracy and reliability.
4. Recommendation Systems: Bayesian updating is essential for refining user preferences in recommendation systems, allowing for more personalized and relevant suggestions.
Advantages and Challenges of Bayesian Updating
One of the significant advantages of Bayesian updating is its ability to incorporate new information efficiently, leading to continuous model improvement. This adaptability is particularly beneficial in dynamic environments where data is constantly evolving. Additionally, Bayesian methods provide a principled way to handle uncertainty and make probabilistic predictions, which are crucial in many machine learning tasks.
However, Bayesian updating also comes with challenges. Computational complexity can be a concern, especially with large datasets or complex models. Calculating the posterior distribution often involves high-dimensional integrations, which can be computationally intensive. Approximation methods, such as Markov Chain Monte Carlo (MCMC) or variational inference, are often employed to address these issues, albeit with their own trade-offs.
Conclusion
Bayesian updating is an essential concept in machine learning, providing a framework for models to evolve and improve as they process new data. By continuously updating beliefs and probabilities, Bayesian methods enable more accurate predictions and insights, making them invaluable in many applications. Despite the computational challenges, the benefits of incorporating uncertainty and adaptability make Bayesian updating a cornerstone of modern machine learning techniques.
Unleash the Full Potential of AI Innovation with Patsnap Eureka
The frontier of machine learning evolves faster than ever—from foundation models and neuromorphic computing to edge AI and self-supervised learning. Whether you're exploring novel architectures, optimizing inference at scale, or tracking patent landscapes in generative AI, staying ahead demands more than human bandwidth.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
👉 Try Patsnap Eureka today to accelerate your journey from ML ideas to IP assets—request a personalized demo or activate your trial now.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com