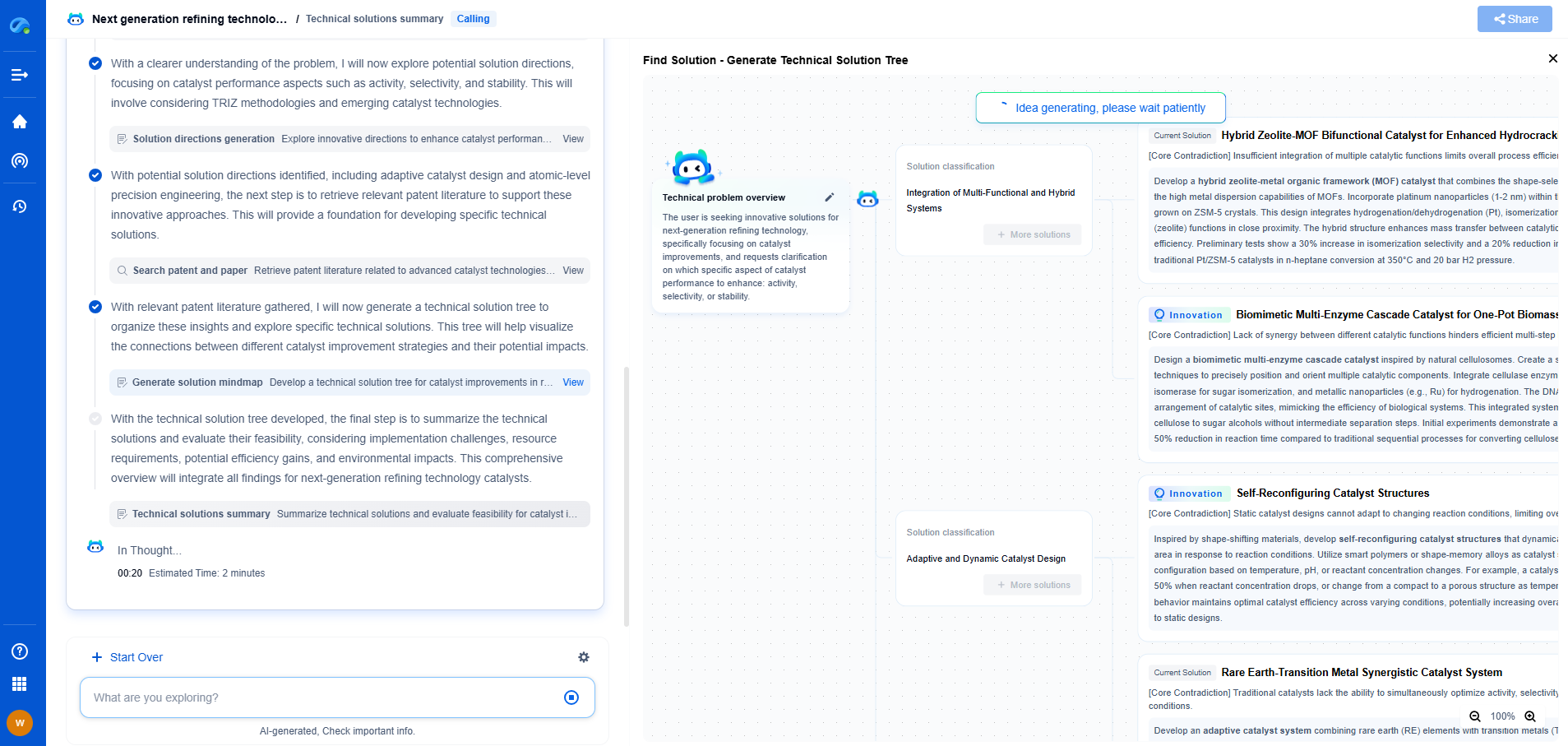
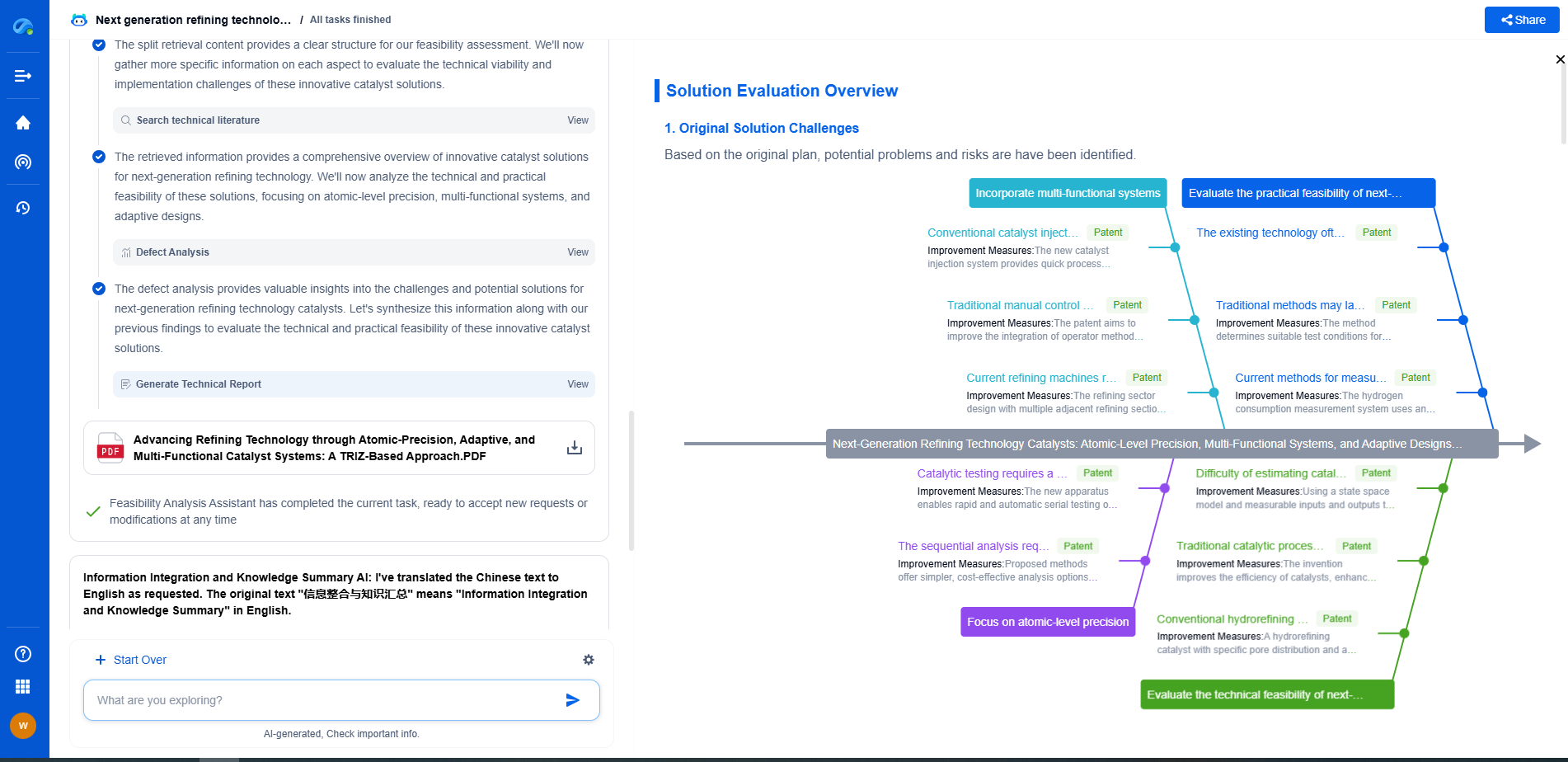
How Optical Flow Estimation Works: Algorithms and Applications
JUL 10, 2025 |
Optical flow estimation is a powerful computational technique used to determine the motion of objects between consecutive frames in a video sequence. It has a wide range of applications in fields such as computer vision, robotics, and video processing. At its core, optical flow estimation seeks to calculate the apparent motion of brightness patterns in an image, allowing for the recognition of movement, depth, and structure within a scene.
The Basics of Optical Flow
Optical flow refers to the pattern of apparent motion of objects in a visual scene, caused by the relative motion between an observer and the scene. Mathematically, it is described as a vector field, where each vector represents the movement of a point in the image over time. The fundamental assumption behind optical flow is that pixel intensities of an object remain consistent as it moves across frames, a concept known as the brightness constancy constraint.
Common Algorithms for Optical Flow Estimation
1. Lucas-Kanade Method
The Lucas-Kanade method is a classic differential technique for optical flow estimation. It assumes that the motion field is smooth and calculates the flow for each pixel by solving a set of linear equations. This method is particularly effective for small motions and regions where movement is relatively uniform. Despite its simplicity, the Lucas-Kanade method remains popular due to its robustness and efficiency in real-time applications.
2. Horn-Schunck Method
The Horn-Schunck approach is another foundational method in optical flow estimation. Unlike the Lucas-Kanade method, it introduces a global smoothness constraint that enforces the flow field to be smooth across the entire image. This method formulates the optical flow estimation as an optimization problem, balancing the brightness constancy constraint with the smoothness constraint. The Horn-Schunck method is well-suited for scenarios where the entire image may have a consistent motion pattern, although it can be sensitive to noise.
3. Farneback Method
The Farneback method is known for its ability to estimate dense optical flow, providing motion information for every pixel in the image. It uses polynomial expansion to model pixel intensities and calculates the displacement field by comparing these models between frames. This method is advantageous in situations where dense and detailed motion information is required, such as in video stabilization and motion tracking.
Applications of Optical Flow Estimation
1. Motion Detection and Tracking
Optical flow estimation plays a crucial role in motion detection and tracking systems. By accurately estimating the movement of objects, systems can identify and follow targets, making it an essential tool in surveillance, traffic monitoring, and human-computer interaction applications.
2. Video Compression
In video compression, optical flow is used to predict the motion between frames, allowing for more efficient encoding of video data. By understanding the movement of objects, compression algorithms can allocate fewer bits to represent changes, reducing the overall size of the video file without sacrificing quality.
3. Autonomous Vehicles
Optical flow estimation is vital for the navigation of autonomous vehicles. It helps these vehicles understand their surroundings, detect obstacles, and make decisions based on the movement of other objects in the environment. This capability is critical for ensuring safe and efficient operation in dynamic and unpredictable settings.
4. Augmented Reality
In augmented reality (AR) applications, optical flow estimation aids in aligning virtual objects with the real world. By tracking the motion of the camera and objects in the scene, AR systems can provide a seamless and immersive experience, allowing virtual elements to interact naturally with the physical environment.
Challenges and Future Directions
Despite its widespread use, optical flow estimation faces several challenges. High computational demands, sensitivity to noise, and difficulties in handling large displacements are common issues that researchers continue to address. Advances in deep learning and machine learning have shown promise in overcoming these challenges, offering more robust and accurate solutions. Future developments in optical flow estimation will likely focus on improving accuracy, reducing computational requirements, and expanding the range of applications.
Conclusion
Optical flow estimation is a fundamental technique in computer vision, with algorithms like Lucas-Kanade, Horn-Schunck, and Farneback providing various approaches to understanding motion in visual data. Its applications span numerous fields, offering valuable insights and capabilities in motion detection, video processing, autonomous navigation, and augmented reality. As technology continues to evolve, optical flow estimation will remain a critical tool in the ongoing quest to understand and interpret the dynamic visual world.
Image processing technologies—from semantic segmentation to photorealistic rendering—are driving the next generation of intelligent systems. For IP analysts and innovation scouts, identifying novel ideas before they go mainstream is essential.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
🎯 Try Patsnap Eureka now to explore the next wave of breakthroughs in image processing, before anyone else does.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com