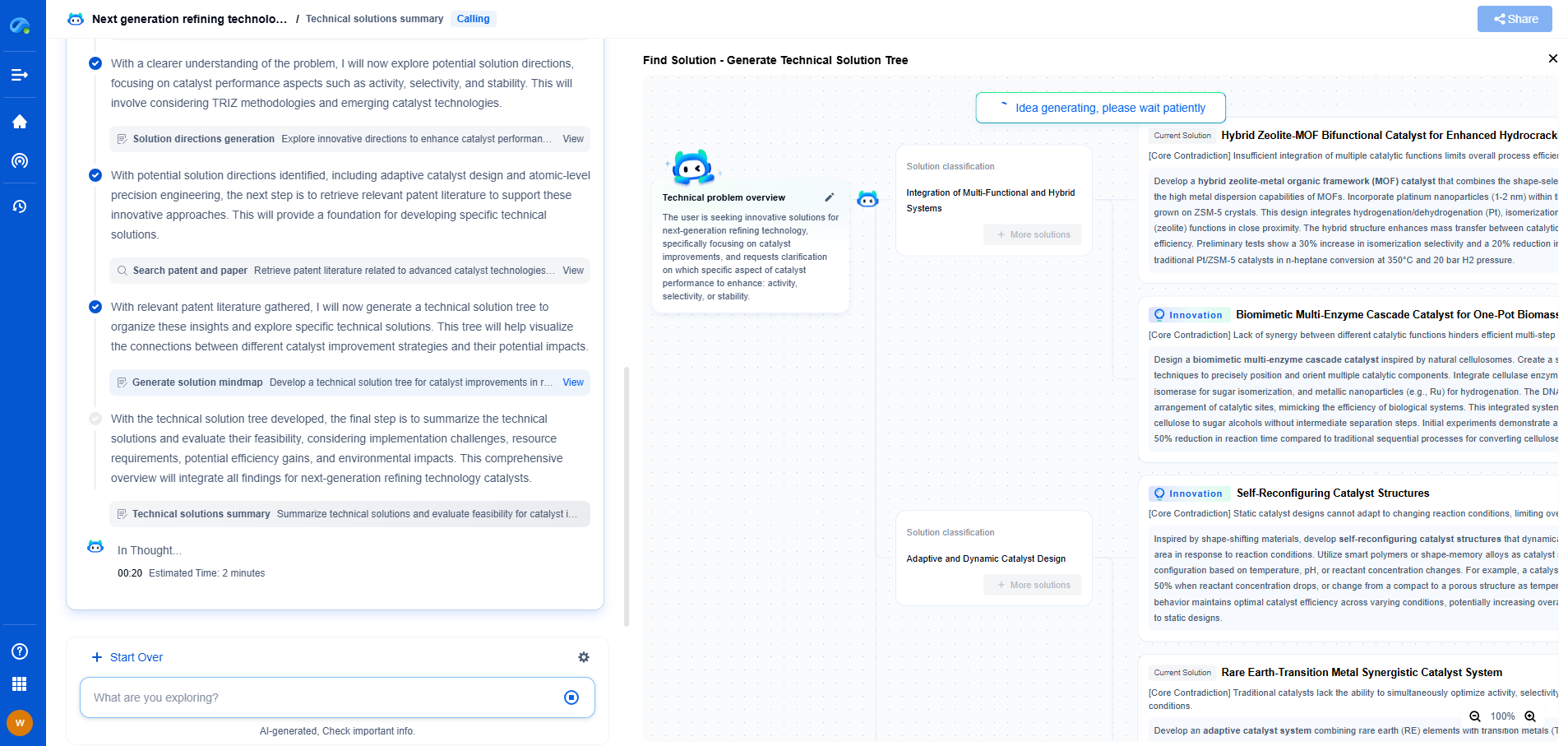
Understanding Reactance and Impedance in AC Circuits

Alternating current (AC) circuits are a fundamental part of many electrical systems, and understanding how they work is essential for anyone involved in electronics or electrical engineering. Two critical concepts in AC circuits are reactance and impedance. Both of these terms describe how components in an AC circuit respond to the flow of alternating current, and they can affect how well the circuit functions. In this blog, we will explore what reactance and impedance are, how to calculate them, and their significance in AC circuits.

What is Reactance?

Reactance is the opposition that inductors and capacitors present to the flow of alternating current. Unlike resistance, which affects both direct current (DC) and AC, reactance only applies to AC and varies with frequency. Reactance is measured in ohms, just like resistance, but it arises from the presence of inductors and capacitors in the circuit rather than resistors.

There are two types of reactance: inductive reactance and capacitive reactance. Inductive reactance occurs in inductors and is caused by the magnetic field that forms around the inductor as current passes through it. Capacitive reactance, on the other hand, occurs in capacitors and results from the electric field created between the plates of the capacitor.

Calculating Inductive Reactance

Inductive reactance (X_L) can be calculated using the formula:

X_L = 2πfL

where:
- X_L is the inductive reactance in ohms,
- f is the frequency of the AC source in hertz (Hz),
- L is the inductance in henrys (H).

This formula highlights that inductive reactance increases with frequency and the inductance of the coil. Therefore, higher frequencies or larger inductors result in greater opposition to the flow of AC.

Calculating Capacitive Reactance

Capacitive reactance (X_C) is calculated using the following formula:

X_C = 1 / (2πfC)

where:
- X_C is the capacitive reactance in ohms,
- f is the frequency of the AC source in hertz (Hz),
- C is the capacitance in farads (F).

In contrast to inductive reactance, capacitive reactance decreases with an increase in frequency or capacitance. This means that capacitors allow more AC to pass through at higher frequencies.

Understanding Impedance

Impedance is the overall opposition that a circuit presents to the flow of AC. It is a combination of resistance and reactance and is also measured in ohms. Unlike resistance, which is purely a scalar quantity, impedance is a complex quantity, consisting of both magnitude and phase angle.

Impedance in a circuit containing resistors, inductors, and capacitors can be represented as a complex number:

Z = R + jX

where:
- Z is the impedance,
- R is the resistance,
- j is the imaginary unit (√-1),
- X is the net reactance (X_L - X_C for a series circuit).

Calculating Impedance in Series Circuits

In a series circuit, the total impedance can be found by adding the resistance and the net reactance. The magnitude of the impedance (|Z|) can be calculated using:

|Z| = √(R² + X²)

The phase angle (θ) of the impedance, which indicates the phase difference between the voltage and the current, is given by:

θ = arctan(X/R)

Calculating Impedance in Parallel Circuits

For parallel circuits, calculating impedance is slightly more complex. The admittance (Y), which is the reciprocal of impedance, is often used:

Y = 1/Z = G + jB

where:
- G is the conductance (1/R),
- B is the susceptance (1/X).

The magnitude and phase angle of the impedance can then be found by calculating the reciprocal of the total admittance.

Importance of Reactance and Impedance

Understanding and calculating reactance and impedance are vital for designing and analyzing AC circuits. These calculations help predict how circuits will behave at different frequencies, which is crucial for applications like filtering, tuning, and impedance matching. Impedance matching, in particular, is essential in audio, radio frequency, and telecommunications to ensure maximum power transfer and minimize signal reflection.

By mastering these concepts, engineers and technicians can better design and troubleshoot AC circuits, leading to more efficient and reliable electrical systems. Whether you're working on a complex electrical grid or a simple audio setup, understanding reactance and impedance is key to success in the world of AC circuits.