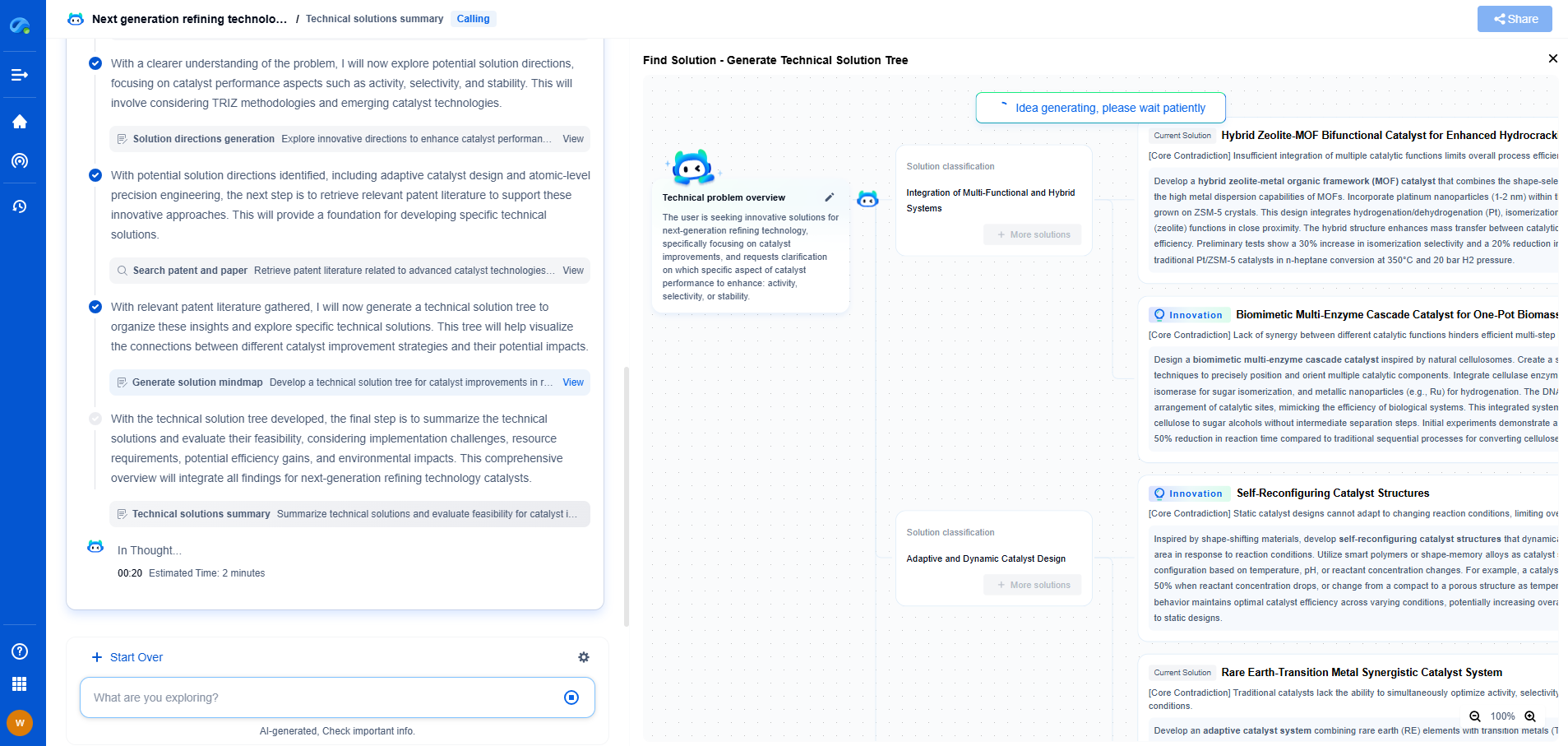
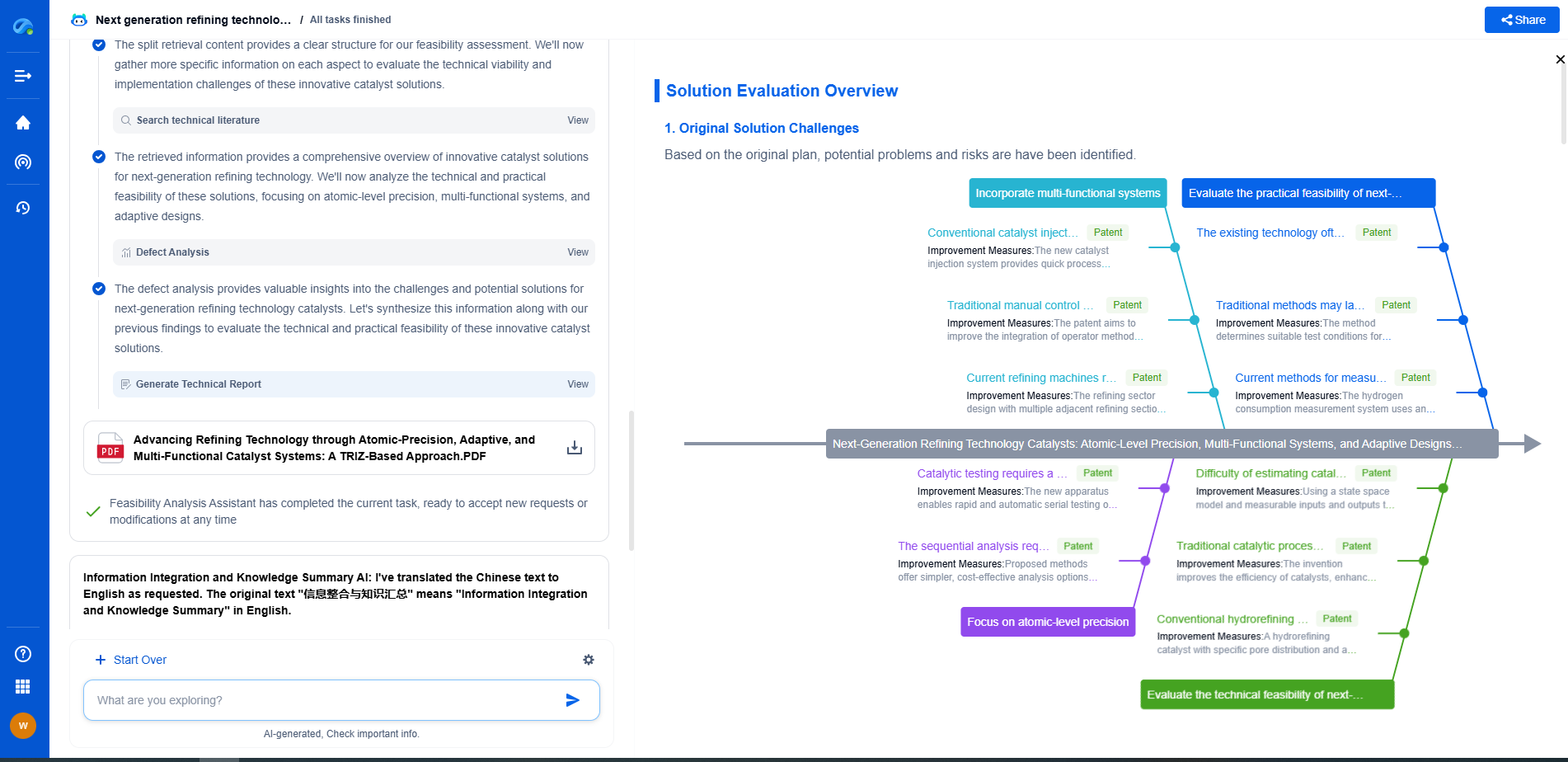
How to Choose FIR Filter Taps for Optimal Noise Reduction
JUL 17, 2025 |
Finite Impulse Response (FIR) filters play a crucial role in digital signal processing, especially when it comes to reducing noise in various applications such as audio processing, communications, and instrumentation. Unlike Infinite Impulse Response (IIR) filters, FIR filters do not rely on feedback and offer distinct advantages in stability and linear-phase response. The process of choosing the right FIR filter taps is essential for achieving optimal noise reduction, ensuring that the signal retains its integrity and quality.
Understanding FIR Filter Taps
FIR filter taps are essentially the coefficients that define the filter's impulse response. These taps determine how the filter processes incoming signals, influencing its ability to effectively reduce noise. The number of taps, also known as the filter's order or length, directly affects the filter's performance characteristics, such as its frequency response and transition bandwidth.
When designing an FIR filter, a higher number of taps generally results in a more selective filter with sharper cutoffs. This translates to better noise reduction capabilities but also increases the computational load. Therefore, striking the right balance between filter complexity and performance is key.
Factors Influencing the Choice of Filter Taps
1. Desired Frequency Response: The primary consideration in selecting FIR filter taps is the desired frequency response. Determine the specific frequencies that need to be attenuated or passed. This will help in deciding the filter's cutoff frequencies and the number of taps required to achieve the desired selectivity.
2. Transition Bandwidth: The transition bandwidth is the range of frequencies over which the filter transitions from passband to stopband. A narrower transition bandwidth usually requires more taps to achieve a sharp transition, which is important for precise noise reduction.
3. Signal Characteristics: Understanding the characteristics of the input signal can guide the selection process. For example, if the signal contains high-frequency noise, a low-pass FIR filter with a sufficient number of taps will effectively attenuate unwanted components while preserving the desired signal.
4. Computational Resources: The number of filter taps directly influences the computational complexity of the filter. Systems with limited processing power or those requiring real-time processing may need to compromise on the number of taps to ensure efficient execution.
Design Techniques for Optimal Noise Reduction
1. Windowing Method: The windowing method is a popular approach for designing FIR filters. By applying a window function to the ideal impulse response, one can manage the trade-off between filter sharpness and side-lobe levels. Common window functions include Hamming, Hanning, and Blackman, each offering different trade-offs in terms of main lobe width and side-lobe attenuation.
2. Parks-McClellan Algorithm: This algorithm is a powerful technique for designing equiripple FIR filters. It provides an optimal solution by minimizing the maximum error between the desired and actual frequency responses. The algorithm allows the designer to specify the number of taps and desired performance, making it a versatile choice for noise reduction applications.
3. Least Squares Method: The least squares method minimizes the overall error across the frequency band, providing a filter with a smooth frequency response. This method is suitable for applications where uniform performance across the frequency band is required.
Evaluating Filter Performance
After designing the FIR filter, it's crucial to evaluate its performance to ensure it meets the noise reduction requirements. Analyze the frequency response to verify that the filter provides the necessary attenuation in the stopband while maintaining minimal distortion in the passband. Additionally, simulate the filter's effect on the actual signal to assess its practical performance.
Conclusion
Choosing the right FIR filter taps is essential for optimal noise reduction in digital signal processing. By considering factors such as desired frequency response, transition bandwidth, signal characteristics, and computational resources, you can design a filter that effectively reduces noise while preserving signal integrity. Employing design techniques like the windowing method, Parks-McClellan algorithm, and least squares method can further enhance filter performance. Ultimately, evaluating the filter's performance ensures that it meets the intended noise reduction goals and contributes to improved signal quality.
Whether you’re developing multifunctional DAQ platforms, programmable calibration benches, or integrated sensor measurement suites, the ability to track emerging patents, understand competitor strategies, and uncover untapped technology spaces is critical.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
🧪 Let Eureka be your digital research assistant—streamlining your technical search across disciplines and giving you the clarity to lead confidently. Experience it today.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com