How to implement Cartesian control in 6-axis robots

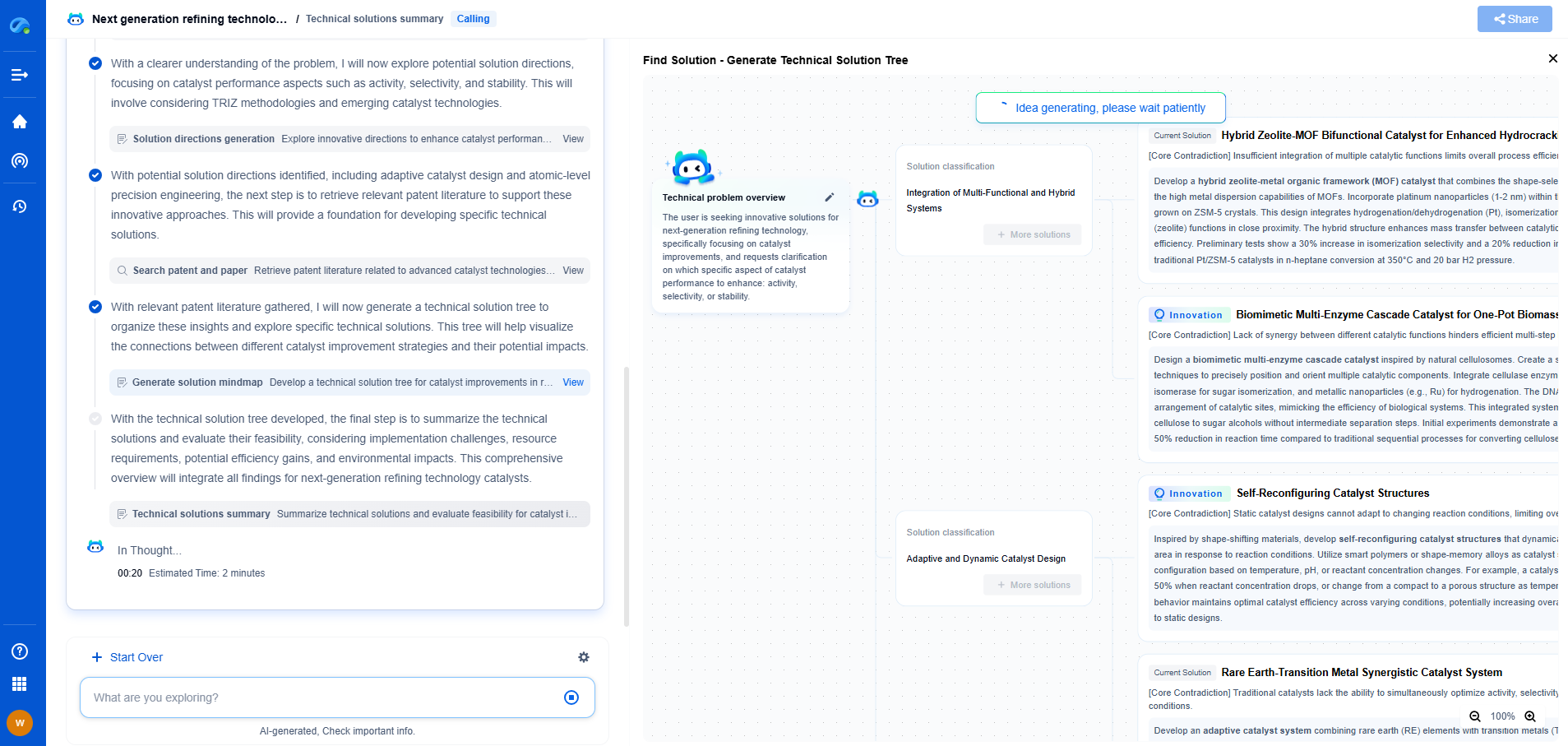
Cartesian control in robotics refers to controlling a robot’s end-effector directly in Cartesian (XYZ) coordinates, rather than joint angles. This approach enables precise positioning and orientation in a 3D workspace by converting desired end-effector motions into joint movements through inverse kinematics. Cartesian control is essential for tasks requiring spatial accuracy, such as welding, assembly, or surgical robotics. It simplifies programming by allowing users to define movements in task space rather than joint space.

Understanding Cartesian Control

Cartesian control involves controlling the position and orientation of the robot's end effector directly in a three-dimensional space. This is in contrast to joint control, which involves moving each joint individually. In Cartesian control, the robot's motion is specified in terms of linear (X, Y, Z) and angular (roll, pitch, yaw) movements, making it easier to visualize and program tasks that require precise positioning.

6-axis robots have six degrees of freedom, allowing them to move in six different ways: three linear movements along the X, Y, and Z axes, and three rotational movements around those axes. This flexibility enables complex tasks like welding, assembly, and packaging.

Benefits of Cartesian Control

1. Intuitive Programming: Cartesian control simplifies the programming process by allowing operators to specify movements in terms of the robot's end effector position, rather than individual joints. This makes it easier to visualize and implement complex tasks.

2. Increased Precision: By controlling the end effector directly, Cartesian control allows for precise positioning and orientation, which is crucial in applications requiring high accuracy.

3. Seamless Integration: Cartesian control can be seamlessly integrated into existing robotic systems, making it an attractive option for industries looking to upgrade their automation processes.

Implementing Cartesian Control in 6-axis Robots

To implement Cartesian control in a 6-axis robot, several steps need to be taken:

1. Kinematic Modeling: The first step is to develop a kinematic model of the robotic arm. This involves understanding the relationship between the robot's joint angles and the position and orientation of the end effector. Forward kinematics calculates the end effector's position from given joint angles, while inverse kinematics determines the joint angles required to achieve a desired position and orientation.

2. Path Planning: Once the kinematic model is established, the next step is path planning. This involves defining the trajectory that the end effector will follow to reach the target position. Path planning algorithms take into account the robot's kinematic constraints, obstacles in the environment, and the desired speed and acceleration profiles.

3. Control Algorithms: Control algorithms play a crucial role in executing the planned path accurately. These algorithms ensure that the robot follows the desired trajectory while compensating for any disturbances or errors. Common control techniques include Proportional-Integral-Derivative (PID) control, Model Predictive Control (MPC), and adaptive control.

4. Simulation and Testing: Before deploying the robot in a real-world application, it is essential to simulate and test the Cartesian control system. Simulation software allows engineers to validate the robot's performance in a virtual environment, identify potential issues, and make necessary adjustments.

5. Calibration and Tuning: Once the system is tested, calibration and tuning are necessary to optimize the robot's performance. This involves adjusting control parameters and ensuring that the robot operates smoothly and accurately in the intended environment.

Challenges and Considerations

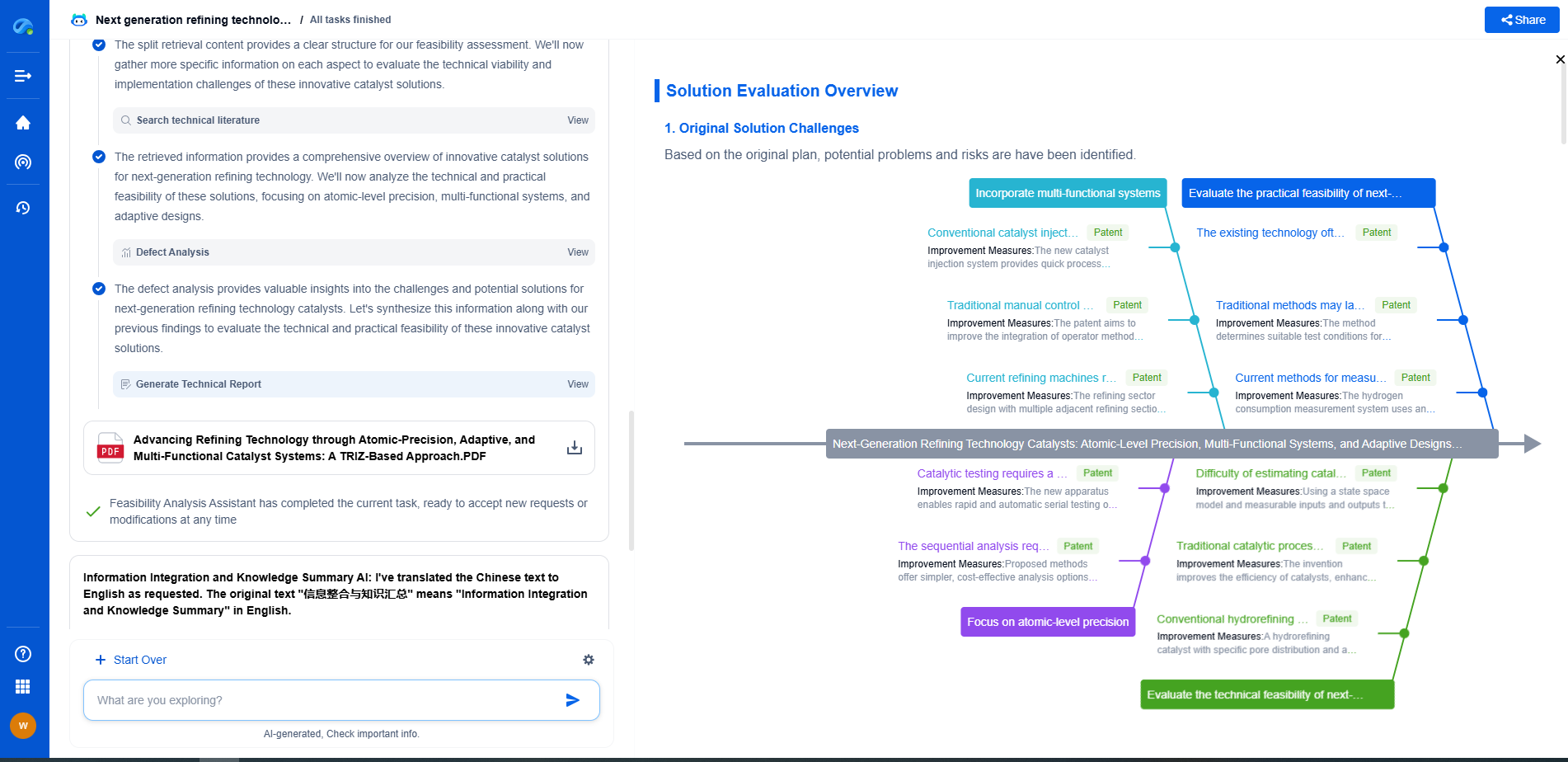
While Cartesian control offers numerous benefits, there are also challenges to consider. One significant challenge is the complexity of inverse kinematics, especially for robots with multiple joints and constraints. Ensuring smooth transitions between different paths and handling singularities (positions where the robot's movements are undefined) can also be challenging.

Additionally, environmental factors such as temperature changes, vibrations, and external forces can impact the robot's performance. Therefore, robust control algorithms and regular maintenance are essential to ensure consistent operation.

Conclusion

Implementing Cartesian control in 6-axis robots can significantly enhance their performance and versatility in various industrial applications. By allowing precise and intuitive control of the robot's end effector, Cartesian control simplifies programming and enables complex tasks to be performed with high accuracy. However, successful implementation requires careful consideration of kinematic modeling, path planning, control algorithms, and environmental factors. With the right approach, Cartesian control can unlock the full potential of 6-axis robots, driving efficiency and innovation in automation.