Understanding the Basics of FFT

The Fast Fourier Transform (FFT) is a powerful computational technique used in signal processing to transform a signal from its original time domain into the frequency domain. This transformation allows for the analysis of the signal's frequency components, making it an invaluable tool in various fields such as audio processing, image analysis, and communications. The FFT is an efficient algorithm that reduces the complexity of direct computation of the Discrete Fourier Transform (DFT) from O(N^2) to O(N log N), where N is the number of data points. In this article, we will delve into the implementation of FFT for signal analysis, exploring its significance, how it works, and how you can use it in practice.

The Significance of Frequency Domain Analysis

Before we dive into the implementation details, it's crucial to understand why transforming a signal into the frequency domain is beneficial. Signals in the time domain can be complex and difficult to analyze, especially when they are composed of multiple frequencies. By converting a signal into the frequency domain, we can easily identify and analyze these individual frequency components. This is particularly useful in applications such as noise reduction, where certain frequencies can be filtered out, or in audio compression, where less critical frequency components can be discarded.

The Mathematics Behind FFT

At the heart of the FFT is the Discrete Fourier Transform (DFT), which decomposes a sequence of values into components of different frequencies. The FFT is an optimized version of the DFT that takes advantage of the periodicity and symmetry properties of the sine and cosine functions used in the decomposition. In essence, the FFT algorithm divides the DFT calculation into smaller parts, recursively breaking down the problem until it becomes manageable. The most common FFT algorithm is the Cooley-Tukey algorithm, which is highly efficient and widely used in practice.

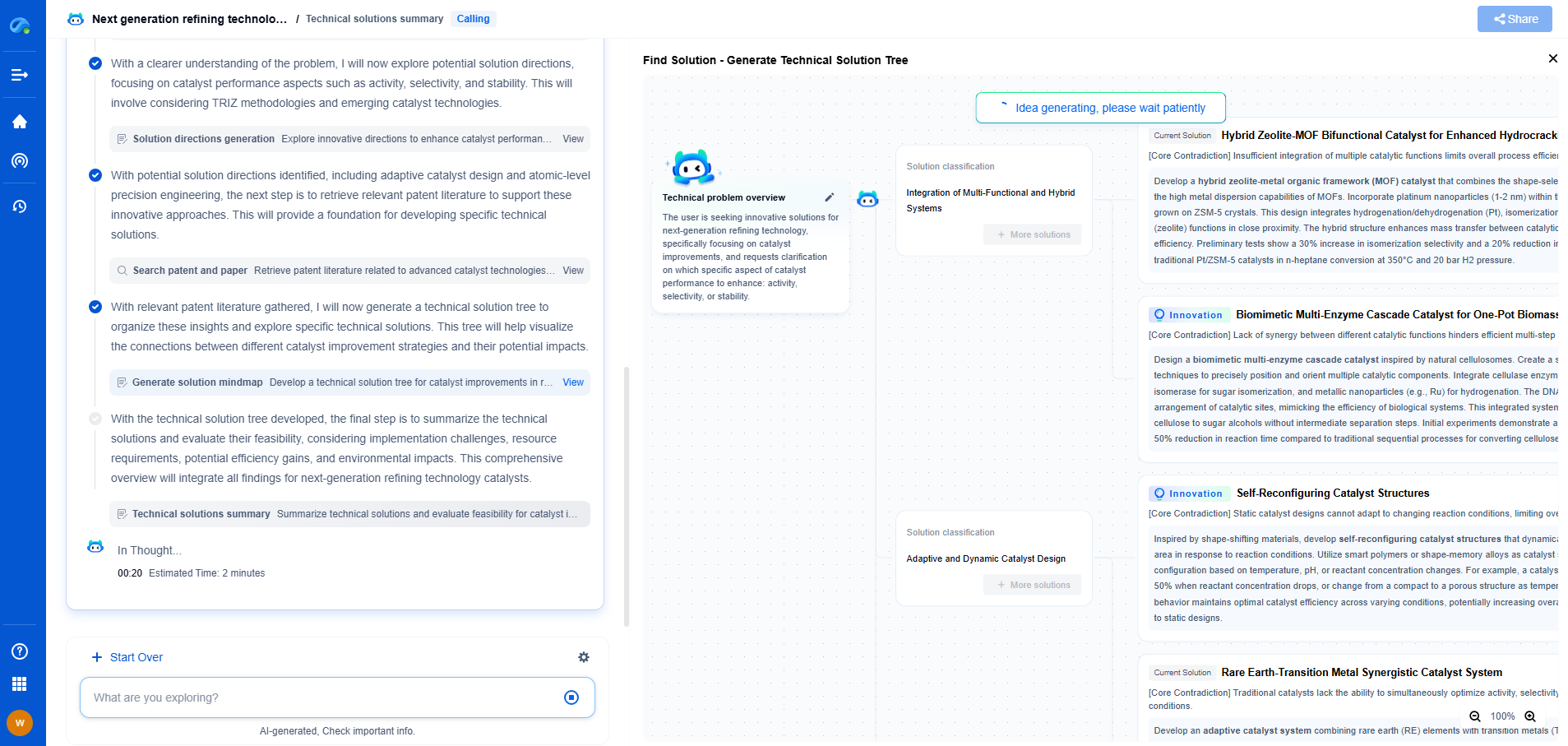
Implementing FFT: A Step-by-Step Guide

1. Prepare Your Data: The first step is to prepare your data for the FFT. Ensure that the number of data points is a power of two, as this is necessary for optimal performance with most FFT algorithms. If your data length is not a power of two, you can pad the signal with zeros to meet this requirement.

2. Choose a Library or Implement from Scratch: Depending on your needs and expertise, you can either use an existing library or implement the FFT algorithm from scratch. Many programming languages, such as Python and MATLAB, offer libraries like NumPy and SciPy that include optimized FFT functions.

3. Perform the FFT: If using a library, you simply need to call the appropriate function with your data. For example, in Python, you can use `numpy.fft.fft()` to perform the FFT on an array of data. If implementing from scratch, follow the Cooley-Tukey algorithm's recursive approach to compute the FFT.

4. Analyze the Results: After performing the FFT, you will obtain a complex-valued array representing the frequency domain of your signal. The magnitude of each complex number corresponds to the amplitude of a particular frequency component, while the phase can give you information about the time shift of the component.

5. Post-Processing: Depending on your signal analysis goals, you might need to perform additional processing. This could involve filtering certain frequencies, analyzing the dominant frequency components, or even applying an inverse FFT to transform the signal back to the time domain after processing.

Practical Applications of FFT

The practical applications of FFT are vast and varied. In audio processing, FFT is used for equalization, sound synthesis, and pitch detection. In telecommunications, it plays a critical role in modulating and demodulating signals. FFT is also essential in medical imaging techniques like MRI and CT scans, where it helps reconstruct images from raw data. Moreover, it is used in vibration analysis and structural health monitoring to identify potential faults in mechanical systems.

Conclusion

The Fast Fourier Transform is a cornerstone of modern signal analysis, offering a fast and efficient way to explore the frequency characteristics of signals. Whether you're a researcher, engineer, or enthusiast in the field of signal processing, understanding and implementing FFT can significantly enhance your ability to analyze and manipulate signals for various applications. By leveraging the power of FFT, you can uncover valuable insights hidden in the frequency domain, enabling you to make informed decisions and innovations in your respective field.