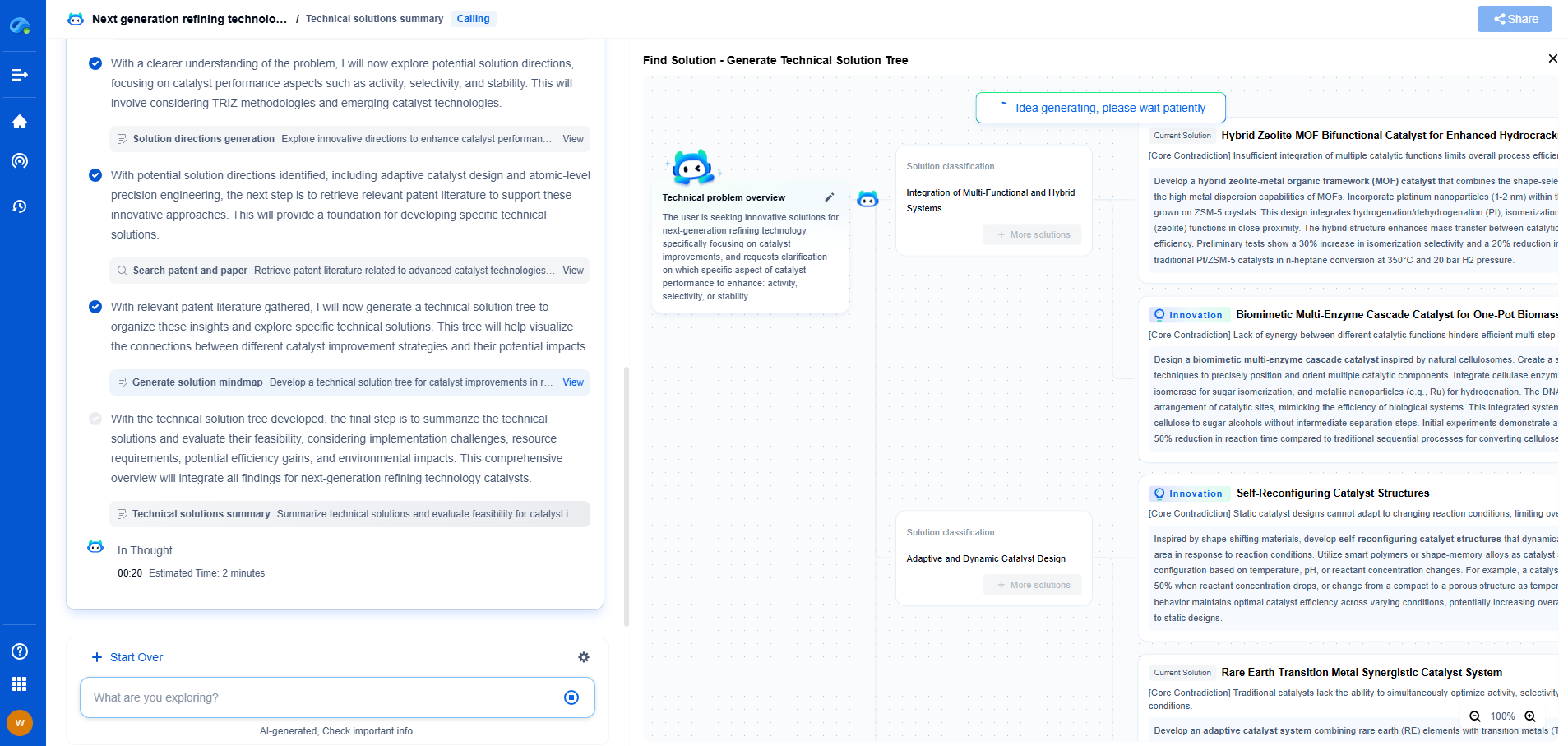
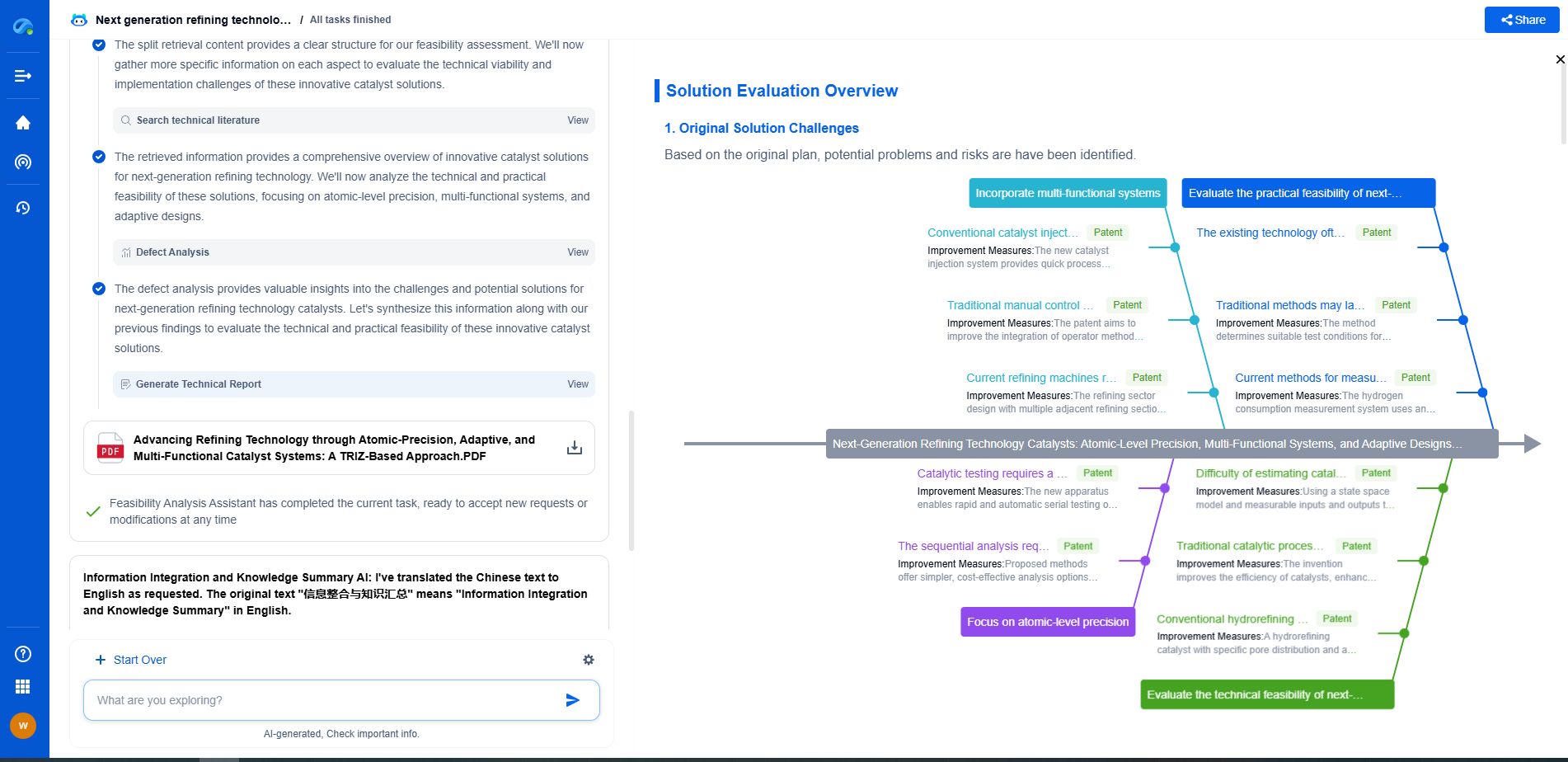
How to Interpret a Confusion Matrix in Machine Learning
JUN 26, 2025 |
The confusion matrix is a crucial tool in the realm of machine learning and statistics, providing a clear visualization of the performance of an algorithm. It is primarily used for evaluating the accuracy of a classification model. At its core, the confusion matrix breaks down the predictions made by a model into four distinct categories. Each of these categories helps us understand where the model is succeeding and where it may be falling short.
Key Components of a Confusion Matrix
A confusion matrix is typically a 2x2 table that outlines the performance of a binary classification model. The rows of the matrix represent the actual classes, while the columns represent the predicted classes. Let's delve into the four critical components:
1. True Positives (TP): These are instances where the model correctly predicts the positive class. For example, if the model predicts a patient has a disease and the patient actually has it, this is a true positive.
2. False Positives (FP): These occur when the model incorrectly predicts the positive class. This is also known as a "Type I error." For instance, if the model predicts a patient has a disease but the patient does not have it, this is a false positive.
3. True Negatives (TN): These are instances where the model correctly predicts the negative class. For example, if the model predicts a patient does not have a disease and the patient indeed does not have it, this is a true negative.
4. False Negatives (FN): These occur when the model incorrectly predicts the negative class. This is also known as a "Type II error." For instance, if the model predicts a patient does not have a disease but the patient actually has it, this is a false negative.
Calculating Performance Metrics
With the basic understanding of the confusion matrix, we can now calculate several performance metrics that help interpret the results and efficiency of a machine learning model.
1. **Accuracy**: This metric indicates the overall effectiveness of a model by measuring the ratio of correctly predicted instances (both true positives and true negatives) to the total number of instances. It is calculated as:
Accuracy = (TP + TN) / (TP + TN + FP + FN)
2. **Precision**: It measures the accuracy of the positive predictions. Precision is especially important in scenarios where the cost of a false positive is high. It is calculated as:
Precision = TP / (TP + FP)
3. **Recall (Sensitivity)**: Also known as sensitivity, it measures the model's ability to correctly identify all positive instances. Recall is critical in circumstances where missing a positive instance is costly. It is calculated as:
Recall = TP / (TP + FN)
4. **F1 Score**: This is the harmonic mean of precision and recall. It provides a balance between the two, especially when the distribution of classes is uneven. It is calculated as:
F1 Score = 2 * (Precision * Recall) / (Precision + Recall)
5. **Specificity**: This metric measures the model's ability to correctly identify all negative instances. It is calculated as:
Specificity = TN / (TN + FP)
Interpreting the Confusion Matrix
The confusion matrix offers a comprehensive view of the model's performance, going beyond mere accuracy. When interpreting the matrix, it is crucial to consider the context of the problem and the consequences of false positives and false negatives. For example, in a medical diagnosis, a false negative might mean a missed disease, which can be more critical than a false positive. On the other hand, for spam detection, a false positive might lead to important emails being marked as spam.
Applications of the Confusion Matrix
The confusion matrix is a versatile tool applicable across various domains. It is widely used in healthcare for disease diagnosis, in finance for fraud detection, in marketing for customer segmentation, and more. By providing a detailed breakdown of the model's performance, it allows data scientists and analysts to fine-tune their models, ensuring higher accuracy and reliability.
Conclusion
Interpreting a confusion matrix is an essential skill for anyone working in machine learning. It not only aids in evaluating model performance but also offers insights that are critical for model improvement. By understanding the intricacies of this matrix and the metrics derived from it, one can make informed decisions to enhance the efficacy of machine learning solutions.
Unleash the Full Potential of AI Innovation with Patsnap Eureka
The frontier of machine learning evolves faster than ever—from foundation models and neuromorphic computing to edge AI and self-supervised learning. Whether you're exploring novel architectures, optimizing inference at scale, or tracking patent landscapes in generative AI, staying ahead demands more than human bandwidth.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
👉 Try Patsnap Eureka today to accelerate your journey from ML ideas to IP assets—request a personalized demo or activate your trial now.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com