Introduction to Integrating Sphere Theory

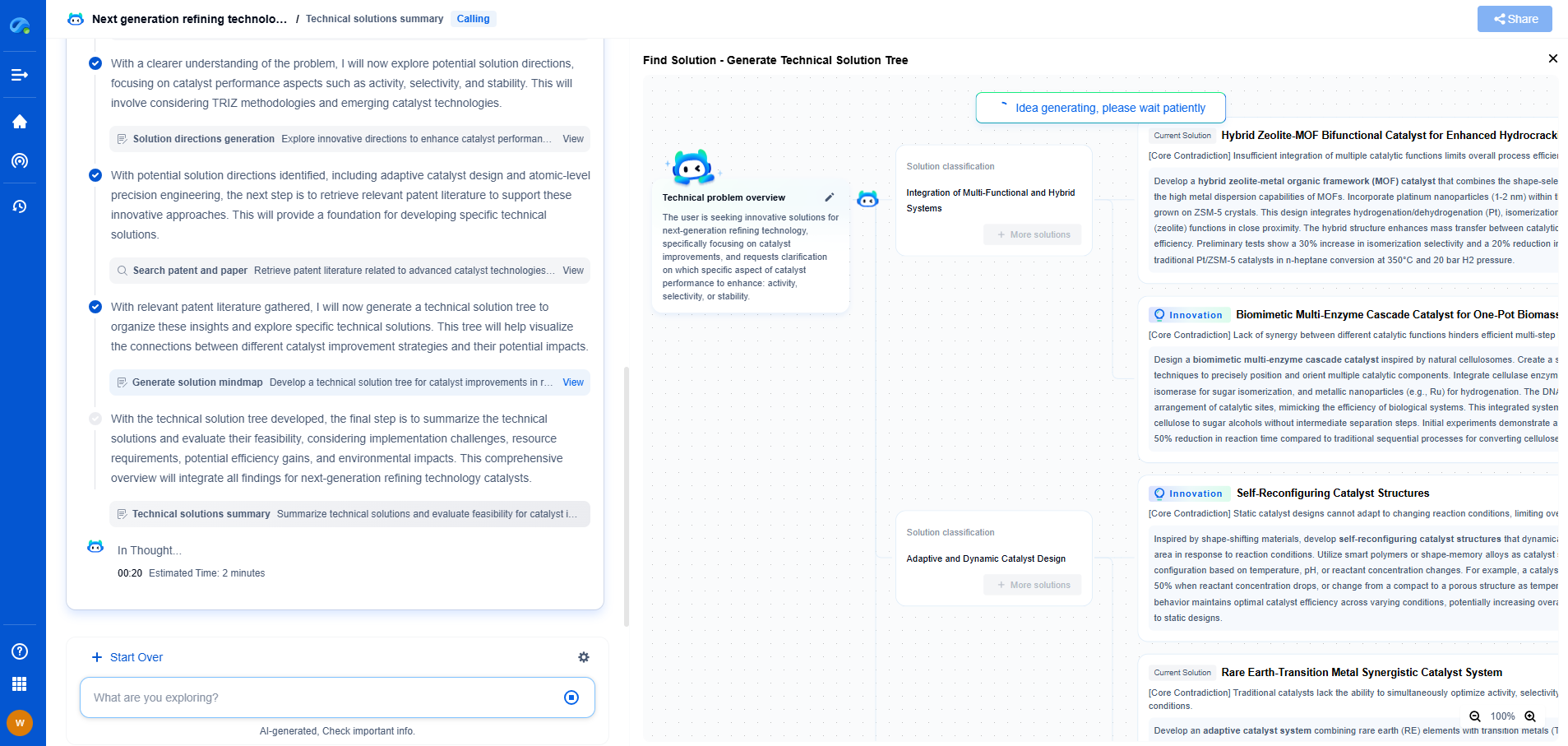
Integrating sphere theory is a fascinating area of study within optical engineering and photometry. Integral to applications in scientific research, manufacturing, and quality control, integrating spheres provide a unique solution to measuring optical properties and achieving uniform light distribution. At the heart of integrating sphere theory is the quest to achieve perfect Lambertian reflection. This article explores the principles behind integrating spheres, the concept of Lambertian reflection, and strategies for achieving near-ideal conditions.

Understanding Lambertian Reflection

Lambertian reflection refers to the phenomenon where light is reflected from a surface such that its intensity is evenly distributed in all directions over a hemisphere. Named after Johann Heinrich Lambert, this ideal reflection is crucial in various optical applications where uniformity in light distribution is required. In practical terms, a Lambertian reflector ensures that the brightness observed is consistent, regardless of the observer's angle, making it invaluable in creating accurate measurements of reflected light.

The Role of Integrating Spheres

Integrating spheres are hollow spherical cavities with diffuse reflective coatings on the interior surface. These coatings are crucial as they scatter incident light uniformly. The primary function of an integrating sphere is to capture light from an external source and uniformly distribute it throughout the sphere's interior. This uniform distribution allows for accurate measurements of the total power of incident light, regardless of its initial direction or distribution.

Key Components of an Integrating Sphere

To comprehend how integrating spheres achieve Lambertian reflection, it's essential to understand their primary components. These include:

1. Sphere Material: The material of the sphere is selected to be highly reflective and diffuse. Common materials include barium sulfate, PTFE (Polytetrafluoroethylene), or specialized coatings that provide near-Lambertian reflectivity.

2. Entrance and Exit Ports: The sphere has strategically positioned ports for light entry and exit. These ports are designed to minimize light loss and ensure that the sphere's interior illumination remains uniform.

3. Detectors: Photodetectors are placed at specific locations to measure the light within the sphere. These detectors help assess the total light power and the uniformity of distribution.

Achieving Perfect Lambertian Reflection

Achieving perfect Lambertian reflection is theoretically ideal rather than practically feasible. However, there are strategies and best practices to approach this ideal:

- Coating Quality: The quality of the sphere's internal coating significantly influences its performance. A highly diffuse and reflective coating enhances the sphere's ability to approximate Lambertian behavior.

- Sphere Geometry: The geometry of the integrating sphere, including the ratio of sphere size to port size, affects its efficiency in distributing light evenly. Careful design considerations ensure minimal deviation from Lambertian characteristics.

- Minimizing Port Losses: Reducing the size and number of ports can limit the loss of light, thus maintaining the sphere's internal uniformity.

Applications of Integrating Spheres

Integrating spheres are utilized across various fields, from calibrating luminance and radiance meters to enhancing the performance of spectrophotometers. Their ability to provide uniform light distribution makes them indispensable in industries like aerospace, automotive, and telecommunications. Moreover, integrating spheres are crucial in environmental testing, where accurate measurements of light emissions play a vital role in monitoring pollution levels.

Conclusion

Integrating sphere theory presents an elegant solution to the challenge of achieving uniform light distribution and accurate optical measurements. While perfect Lambertian reflection remains an ideal, the design and application of integrating spheres continue to push the boundaries of what is achievable in optical science. By understanding and applying these principles, engineers and scientists can enhance the precision and reliability of their optical systems, leading to advancements across numerous technological and scientific domains.