KAN (Kolmogorov-Arnold Networks): The New Challenger to MLPs?
JUN 26, 2025 |
In the rapidly evolving field of artificial intelligence, new architectures and models frequently emerge, challenging established norms and pushing the boundaries of what machines can achieve. One of the latest contenders in this dynamic landscape is Kolmogorov-Arnold Networks (KANs), which are gaining attention for their unique approach to solving complex problems. As we delve into the intricacies of KANs, it’s imperative to explore how they compare to the widely-used Multi-Layer Perceptrons (MLPs), and whether they might indeed pose a threat to the dominance of traditional neural networks in certain applications.
Understanding the Basics of KANs
Named after the mathematicians Andrey Kolmogorov and Vladimir Arnold, Kolmogorov-Arnold Networks build upon the Kolmogorov-Arnold representation theorem. This theorem states that any continuous function can be represented by a finite sum of continuous functions of one variable. KANs leverage this theorem by utilizing a network architecture that is potentially less complex than traditional MLPs but still capable of universal approximation.
A typical KAN architecture consists of several layers of nonlinear functions that are adept at approximating complex, high-dimensional functions with fewer parameters. This reduction in complexity can lead to faster training times and lower computational costs, making KANs an attractive alternative, especially in resource-constrained environments.
The Appeal of Simplicity
One of the most compelling advantages of KANs lies in their simplicity. Traditional neural networks, such as MLPs, often require multiple layers and a significant number of neurons to achieve high precision in function approximation. This complexity can lead to overfitting, increased computational demands, and the need for extensive hyperparameter tuning.
In contrast, KANs use a more straightforward approach by focusing on the intrinsic ability of Kolmogorov-Arnold representations to encapsulate complex functions with fewer parameters. This simplicity not only reduces the risk of overfitting but also enhances the interpretability of the model, allowing researchers and practitioners to gain better insights into the underlying mechanics of the network.
Performance Considerations
While the theoretical foundations of KANs are promising, performance in practical applications remains a crucial consideration. In scenarios where data is abundant and computational resources are plentiful, MLPs might still be the preferred choice due to their proven efficacy and flexibility. However, in situations where computational efficiency and model interpretability are paramount, KANs have the potential to shine.
Recent studies have shown that KANs can outperform traditional MLPs in specific tasks, particularly when dealing with low-dimensional data or when the goal is to achieve a balance between model complexity and accuracy. Moreover, their ability to generalize well on smaller datasets makes them an attractive option for applications where data availability is limited.
Challenges and Future Directions
Despite their promising attributes, KANs are not without challenges. One of the primary hurdles is the relative novelty of the architecture, which means that many practitioners are still unfamiliar with its intricacies and potential pitfalls. Additionally, while KANs offer a compelling alternative to MLPs, they may not be suitable for all types of data or tasks, particularly those requiring deep and complex hierarchical feature extraction.
Looking ahead, continued research and experimentation will be essential to fully understand the capabilities and limitations of KANs. As the artificial intelligence community explores this new frontier, improvements in training algorithms, model optimization, and real-world applications will likely emerge, further solidifying the role of KANs in the AI landscape.
Conclusion
Kolmogorov-Arnold Networks represent an exciting development in the field of neural networks, offering a streamlined and potentially more interpretable alternative to traditional MLPs. While they may not yet pose a universal challenge to MLPs across all domains, their unique attributes make them a valuable addition to the toolkit of AI practitioners. As research progresses and the understanding of KANs deepens, it will be intriguing to see how these networks evolve and where they find their niche in the broader context of artificial intelligence.
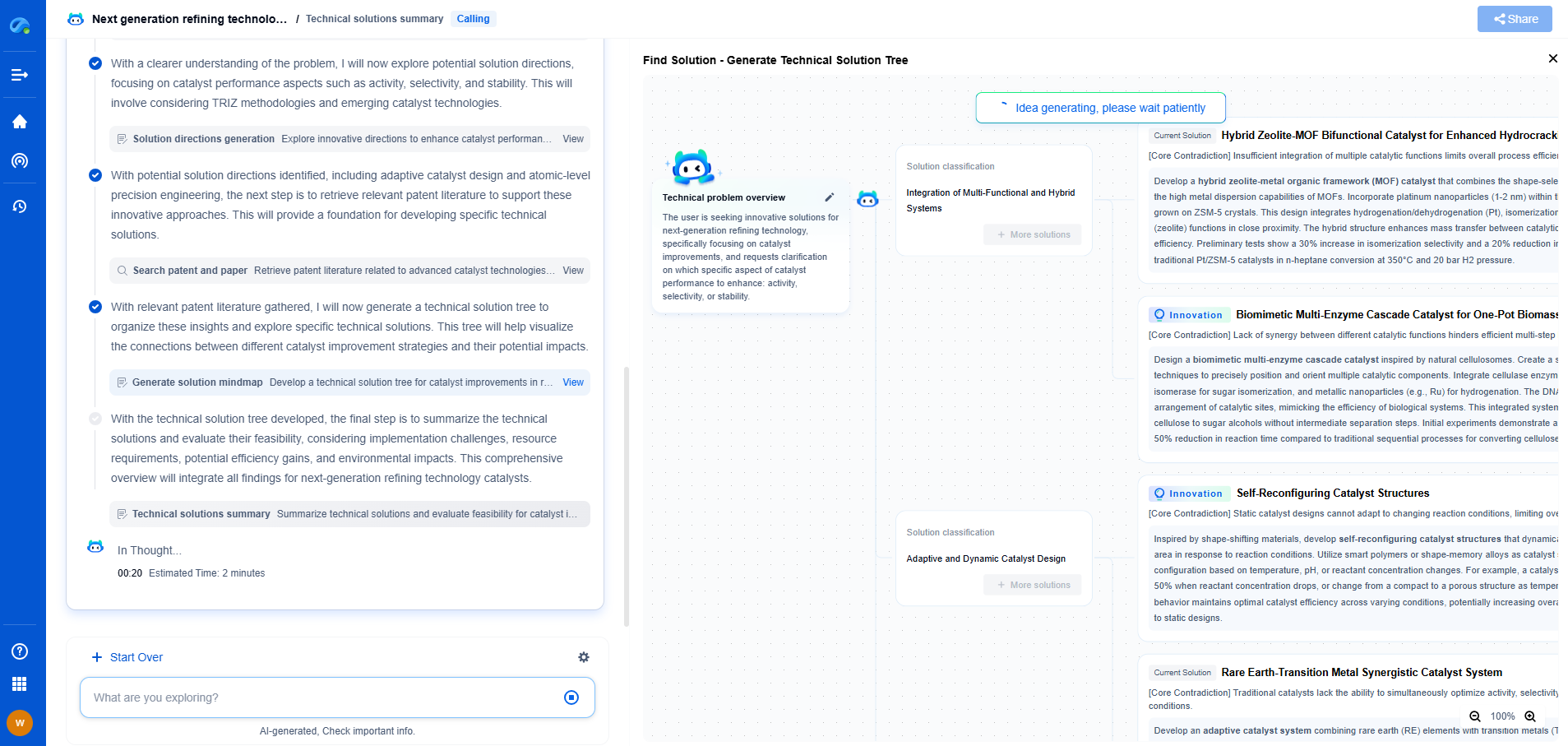
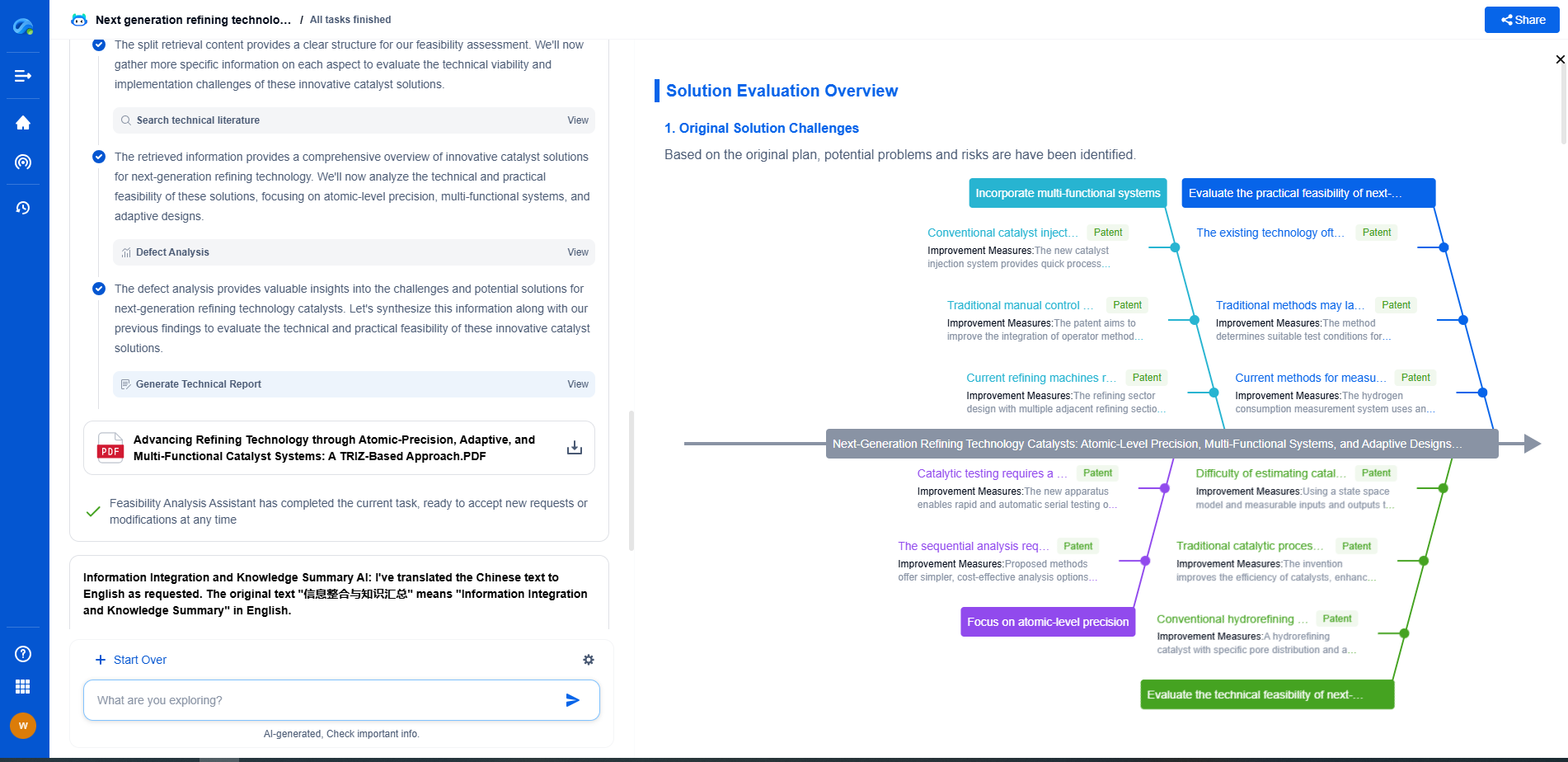
Unleash the Full Potential of AI Innovation with Patsnap Eureka
The frontier of machine learning evolves faster than ever—from foundation models and neuromorphic computing to edge AI and self-supervised learning. Whether you're exploring novel architectures, optimizing inference at scale, or tracking patent landscapes in generative AI, staying ahead demands more than human bandwidth.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
👉 Try Patsnap Eureka today to accelerate your journey from ML ideas to IP assets—request a personalized demo or activate your trial now.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com