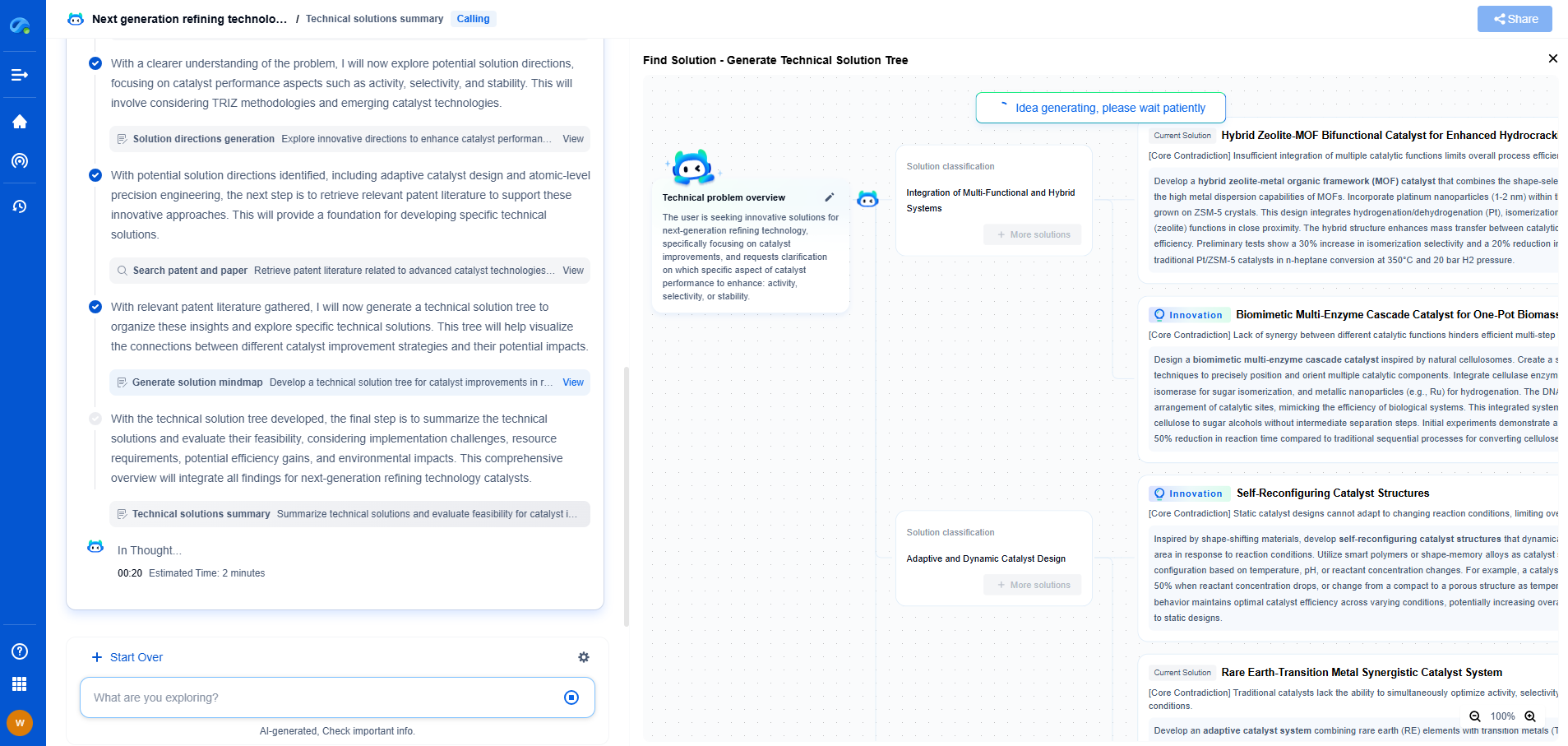
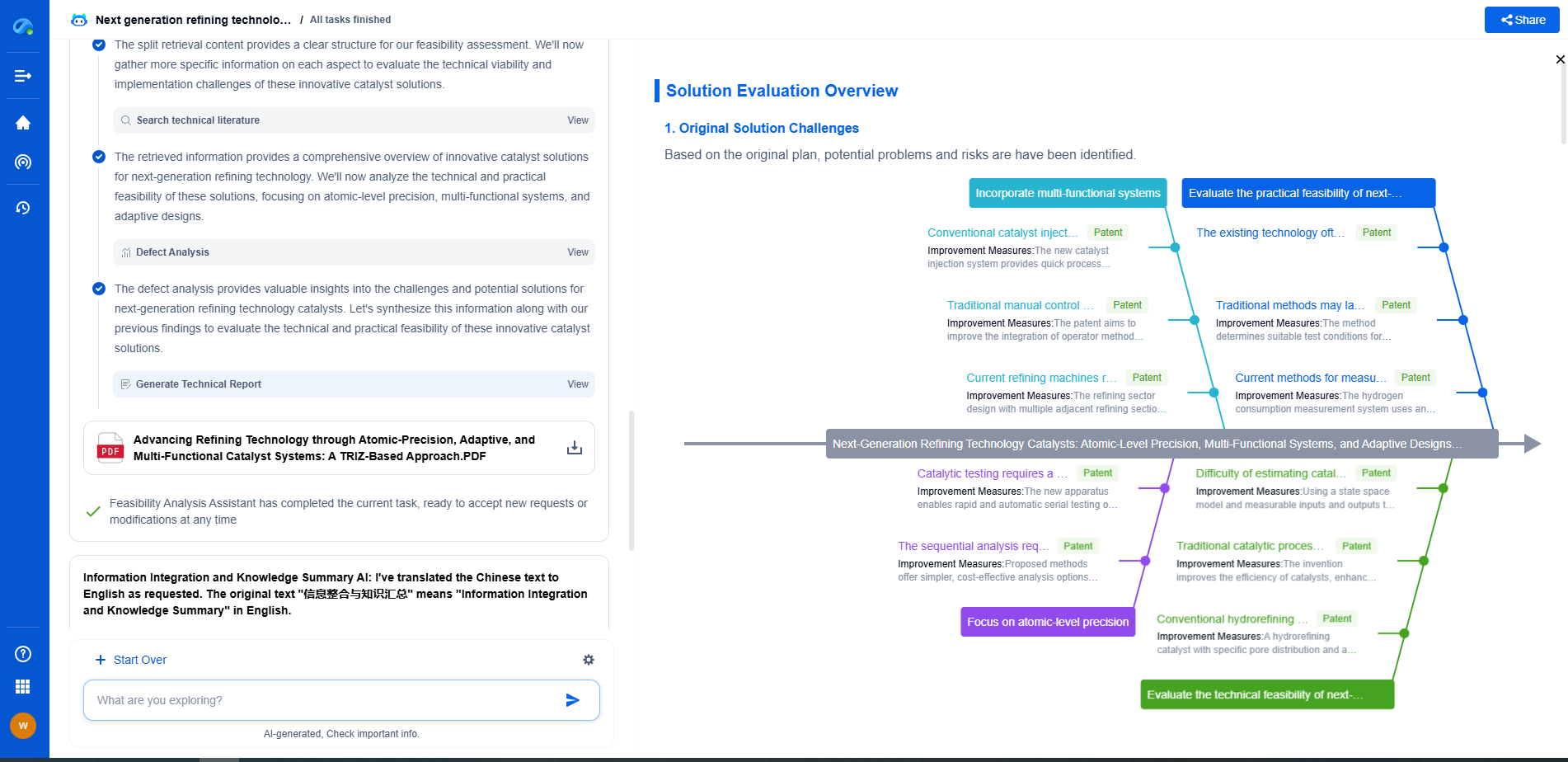
Langmuir vs. Freundlich vs. BET: Isotherm Accuracy for Different Adsorbents
JUL 25, 2025 |
Adsorption is a crucial process in various applications, from water purification to gas capture and storage. Understanding how adsorbates interact with surfaces is vital for optimizing these processes. Three primary models have been developed to describe adsorption isotherms: Langmuir, Freundlich, and BET. Each model has its unique assumptions and applicability, making them suitable for different adsorbents and conditions. This blog delves into the nuances of these models and evaluates their accuracy for various adsorbents.
The Langmuir Isotherm
The Langmuir isotherm is one of the earliest and most widely used models for adsorption. It assumes that adsorption occurs at specific homogeneous sites within the adsorbent and forms a monolayer. The model follows the equation:
\[ q_e = \frac{q_m K_L C_e}{1 + K_L C_e} \]
where \( q_e \) is the amount adsorbed, \( q_m \) is the maximum adsorption capacity, \( K_L \) is the Langmuir constant, and \( C_e \) is the equilibrium concentration.
This model is particularly effective for describing adsorption processes on surfaces with uniform energies of adsorption, such as those found in gas-phase adsorption on solid surfaces. However, it falls short when dealing with multi-layer adsorption or when the surface is heterogeneous.
Application and Limitations of the Freundlich Isotherm
Freundlich isotherm, a more empirical model, was developed to address some of the limitations of the Langmuir isotherm. It is described by the equation:
\[ q_e = K_F C_e^{1/n} \]
where \( K_F \) and \( 1/n \) are constants indicative of the adsorption capacity and intensity, respectively.
The Freundlich model does not assume a homogeneous surface or a monolayer capacity, making it more versatile for various adsorbents and conditions. It is particularly useful for adsorption on heterogeneous surfaces and in cases where the adsorption capacity varies with concentration. However, this model does not predict a saturation point, which can be a limitation in certain scenarios.
Exploring the BET Isotherm
The Brunauer, Emmett, and Teller (BET) isotherm extends the Langmuir model to multilayer adsorption. It is expressed as:
\[ \frac{C_e}{(q_e(q_m - q_e))} = \frac{1}{q_m C_s} + \left(\frac{C_e}{q_m C_s}\right) \]
where \( C_s \) is the saturation concentration. The BET model is particularly suitable for physical adsorption processes involving gas on solid surfaces where multiple layers of adsorbate molecules are possible.
This model is widely used for surface area determination of solids. However, its complexity and assumptions about the uniformity and independence of adsorption layers can limit its applicability to certain systems.
Comparative Analysis for Different Adsorbents
When evaluating which isotherm model to use, the nature of the adsorbent and the specific conditions must be considered. For instance, materials with uniform surface properties, such as certain zeolites or activated carbons, might be well-represented by the Langmuir model. On the other hand, materials with a broad distribution of pore sizes, like some clays and natural soils, might be better described by the Freundlich isotherm.
The BET model is often chosen for applications where the primary interest lies in understanding multilayer adsorption, such as in the characterization of porous materials and catalysts.
Conclusion
In conclusion, the choice between the Langmuir, Freundlich, and BET isotherms depends heavily on the specific characteristics of the adsorbent and the system conditions. While the Langmuir model is ideal for simple systems with homogeneous adsorbent sites, the Freundlich model provides more flexibility for heterogeneous systems. The BET isotherm, with its ability to describe multilayer adsorption, is indispensable for studying complex adsorption phenomena.
Ultimately, the isotherm that provides the most accurate representation will depend on the precise nature of the adsorbent, adsorbate, and the conditions under which the adsorption occurs. Researchers and engineers must carefully consider these factors when selecting an appropriate model to ensure optimal process design and operation.
From next-generation membrane materials to high-efficiency separation processes for pharmaceuticals, water treatment, food processing, or energy systems, the filtration & separation industry is rapidly evolving with a surge in material innovation, microstructure design, and process optimization.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
Whether you're designing the next high-throughput filter, optimizing nanostructured surfaces, or exploring new separation media for emerging industries—Patsnap Eureka gives you AI-driven insights in seconds, helping you move from ideation to innovation with confidence.
🚀 Start your free trial today and experience how Eureka transforms filtration innovation—from reactive to predictive.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com