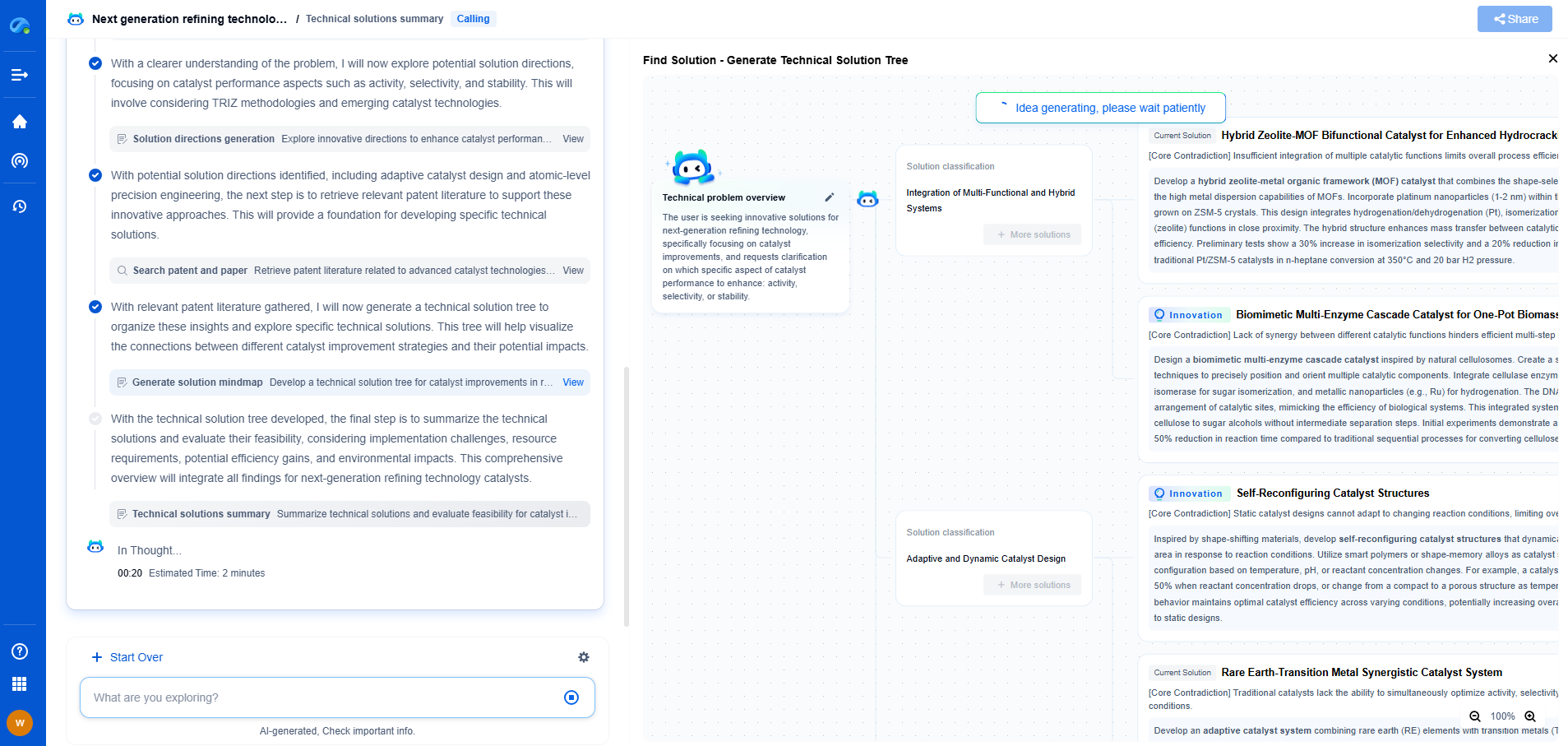
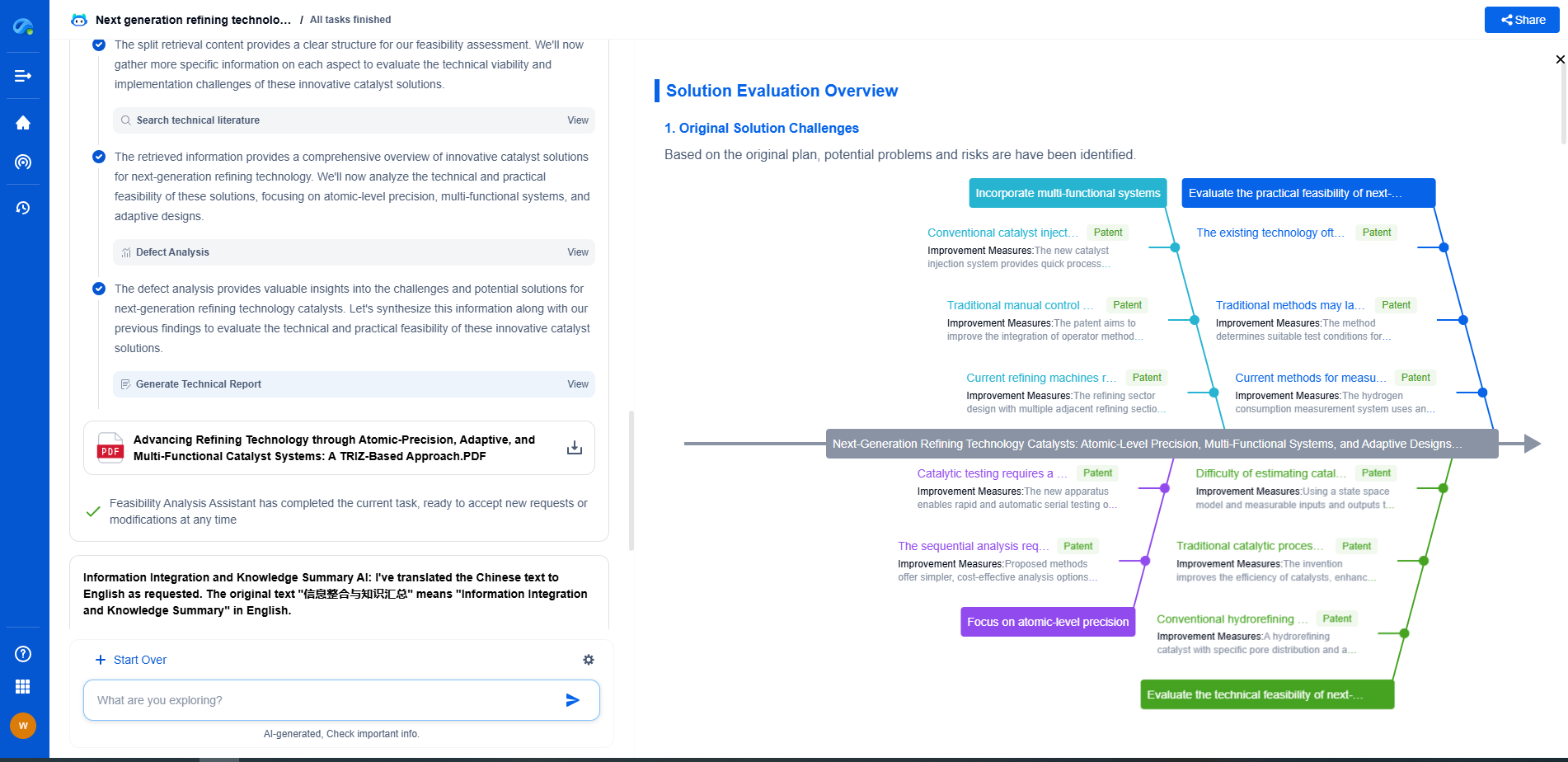
Modal Parameters 101: Natural Frequencies, Mode Shapes, and Damping Ratios
JUL 16, 2025 |
When discussing the dynamic behavior of structures and mechanical systems, modal parameters play a critical role. These parameters, including natural frequencies, mode shapes, and damping ratios, are essential for predicting how structures will respond to various excitations. Whether you're an engineer, architect, or simply curious about mechanical vibrations, understanding these concepts is crucial for analyzing and designing stable and efficient systems.
Natural Frequencies
Natural frequencies are the specific frequencies at which a system tends to vibrate when it is disturbed. Every structure or mechanical system has its unique set of natural frequencies, much like musical instruments have specific notes they can produce. These frequencies are determined by the mass and stiffness of the system. For example, a tuning fork has a specific natural frequency at which it vibrates when struck, producing a clear tone.
In engineering, identifying the natural frequencies of a structure is vital. If a structure is subjected to external forces that match its natural frequencies, resonance occurs, leading to large amplitude vibrations. This can cause significant damage or even structural failure. Thus, engineers strive to design systems where the natural frequencies are well away from the frequencies of any expected external excitations.
Mode Shapes
While natural frequencies tell us how often a system vibrates, mode shapes describe the pattern of deformation during each vibrational mode. Mode shapes illustrate how different parts of a structure move relative to each other at a given natural frequency. Visualizing mode shapes can provide insights into which parts of a structure might experience the most stress or displacement during vibrations.
For example, consider a simple beam. Its mode shape at one of its natural frequencies may show the beam bending in a sinusoidal pattern. Understanding these patterns helps engineers reinforce or modify parts of a structure that are susceptible to excessive movement or stress.
Damping Ratios
Damping is another crucial aspect of system dynamics. It refers to the dissipation of energy in a vibrating system, gradually reducing the amplitude of vibrations over time. Damping ratios are dimensionless quantities that describe how oscillations in a system decay after an external force is removed. A higher damping ratio means that the system will return to rest more quickly, while a lower ratio indicates prolonged vibrations.
Effective damping is critical for mitigating the adverse effects of resonance. Engineers often incorporate damping mechanisms into structures to absorb energy and prevent excessive vibrations. Various materials and techniques, such as viscoelastic materials and tuned mass dampers, are employed to enhance a system's damping characteristics.
Applications and Implications
The practical applications of modal analysis are vast and varied. In the automotive industry, understanding the modal parameters of a vehicle's components can lead to designs that minimize vibrations and noise, improving both performance and comfort. In civil engineering, modal analysis helps in designing buildings and bridges that can withstand earthquakes and strong winds by ensuring that their natural frequencies do not align with those of potential external forces.
In aerospace, the analysis of modal parameters ensures that aircraft structures can endure the dynamic loads encountered during flight. Modal testing and analysis also play a crucial role in the development of electronic devices, where vibrations can affect performance and longevity.
Conclusion
Modal parameters—natural frequencies, mode shapes, and damping ratios—are fundamental to understanding and controlling the dynamic behavior of structures and mechanical systems. By accurately identifying and analyzing these parameters, engineers can design structures that are safe, efficient, and resilient against a wide range of dynamic excitations. Whether it's preventing the catastrophic failure of a suspension bridge or ensuring the smooth operation of a high-performance car, the study of modal parameters is a cornerstone of modern engineering practices.
In the world of vibration damping, structural health monitoring, and acoustic noise suppression, staying ahead requires more than intuition—it demands constant awareness of material innovations, sensor architectures, and IP trends across mechanical, automotive, aerospace, and building acoustics.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
⚙️ Bring Eureka into your vibration intelligence workflow—and reduce guesswork in your R&D pipeline. Start your free experience today.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com