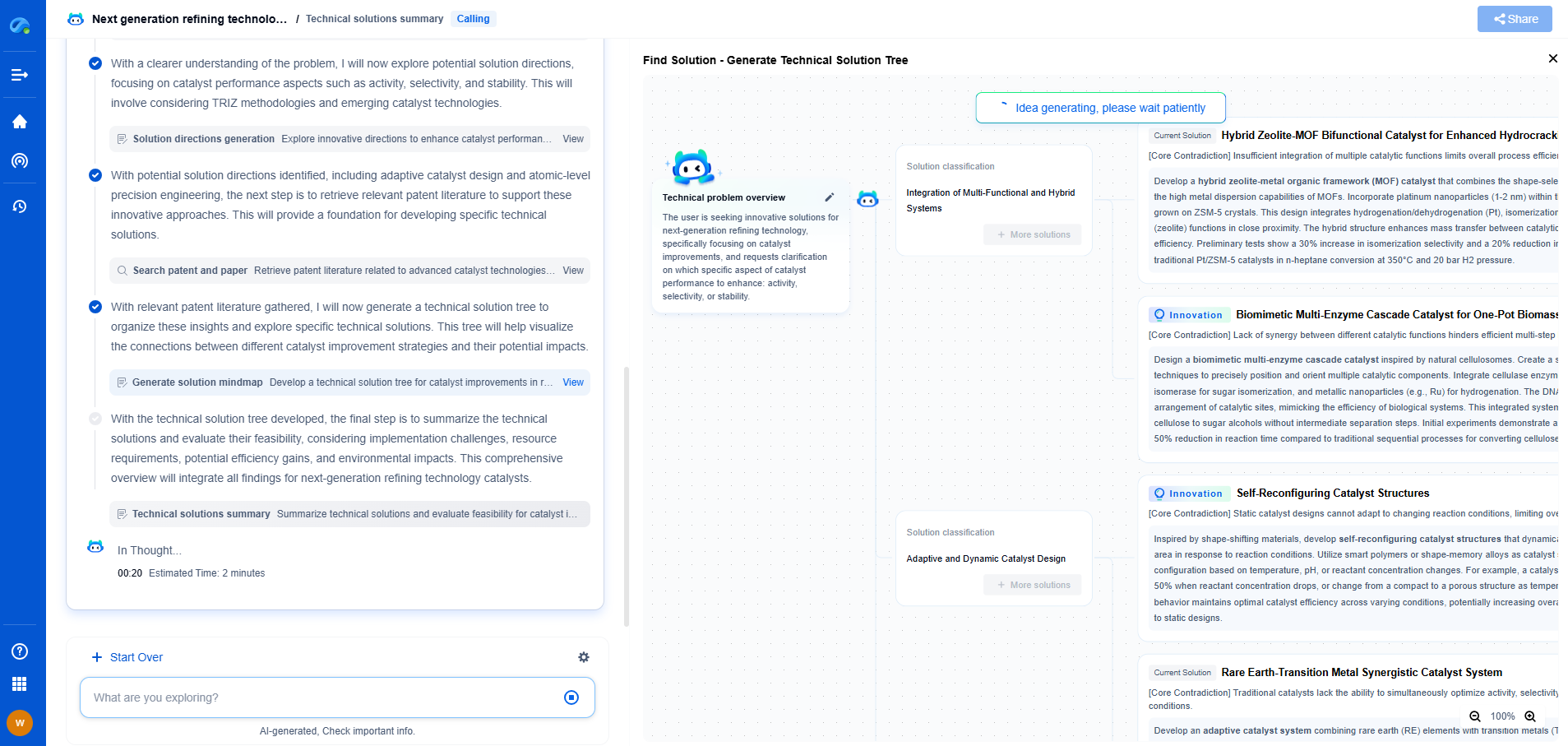
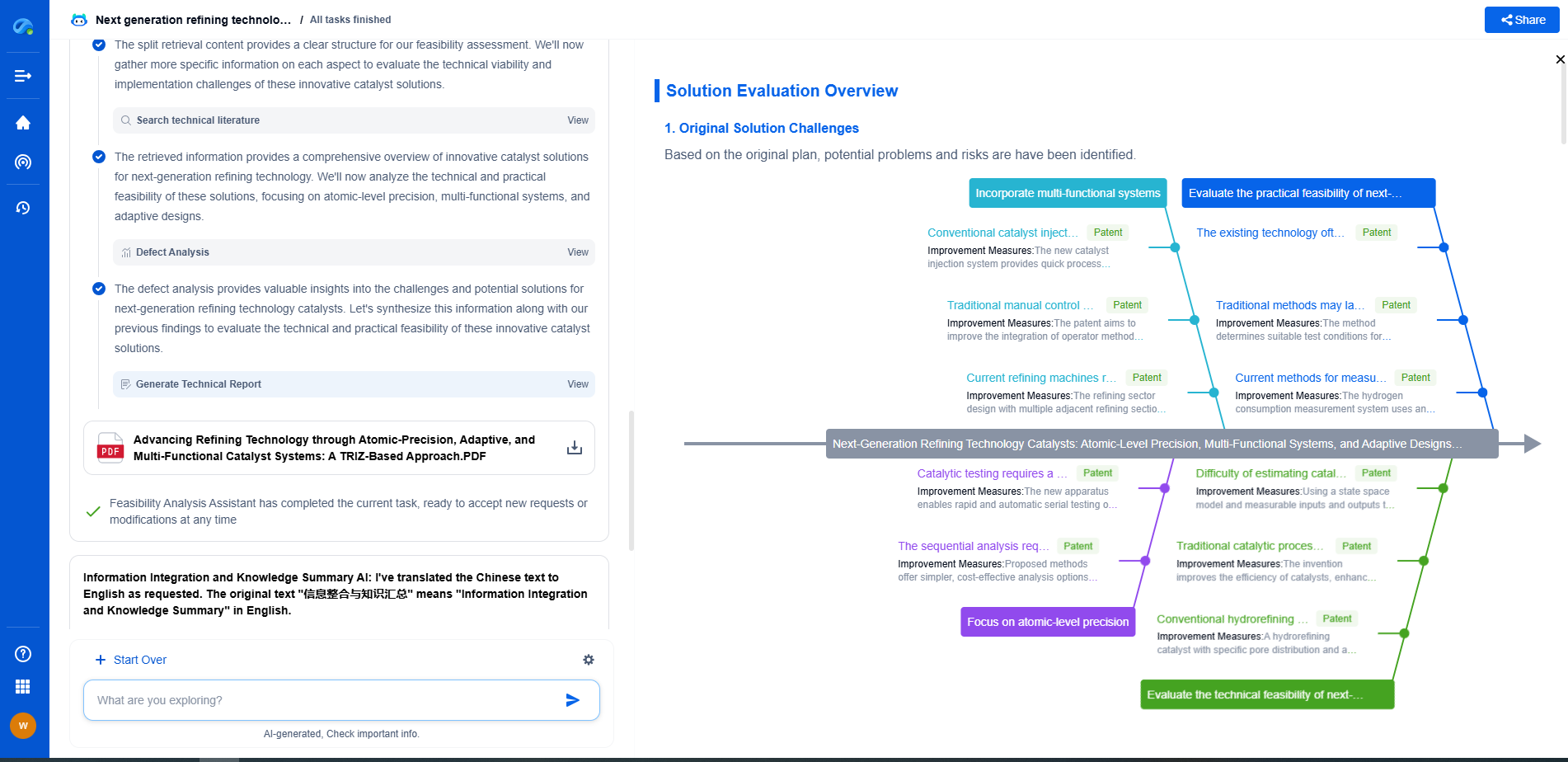
PID Control for Robots: Tuning Gains for Stable Motion
JUN 26, 2025 |
In the world of robotics, achieving stable and precise motion is crucial. This is where PID control, or Proportional-Integral-Derivative control, comes into play. PID controllers are widely used in robotics to manage motion by adjusting the control inputs based on the difference between the desired and actual performance. This feedback loop helps in correcting errors and maintaining stability, making PID control a staple in robotic motion control systems.
Understanding the Basics of PID Control
PID control combines three distinct actions: proportional, integral, and derivative.
1. Proportional Control (P): This component provides a control action proportional to the error signal. The proportional gain (Kp) determines the reaction to the current error. A higher Kp results in a more aggressive response, but it can also lead to overshooting and instability if not managed properly.
2. Integral Control (I): The integral part sums up the past errors and integrates them over time, which helps eliminate the residual steady-state error. The integral gain (Ki) is critical in ensuring that the system eventually reaches the desired setpoint. However, too high a Ki can cause oscillations and instability.
3. Derivative Control (D): The derivative component predicts future errors based on the current rate of error change. It acts as a form of damping, reducing the overshoot caused by the proportional control. The derivative gain (Kd) helps stabilize the system but can introduce noise sensitivity if set too high.
Tuning PID Gains for Optimal Performance
Effective tuning of PID gains is essential for achieving the desired balance between speed and stability in robotic motion. Tuning involves adjusting Kp, Ki, and Kd to achieve optimal performance without causing instability or excessive oscillations.
1. Ziegler-Nichols Tuning Method: This popular method involves setting Ki and Kd to zero initially and increasing Kp until the system oscillates at a constant amplitude. This point is known as the ultimate gain (Ku) and the oscillation period is the ultimate period (Tu). Based on these, initial PID gains are set using Ziegler-Nichols tuning rules.
2. Trial and Error: Although time-consuming, trial and error is a common approach in practical scenarios. It involves manually adjusting the PID parameters and observing the system response to find an optimal balance.
3. Software-Based Tuning: Advanced software tools use algorithms to automatically adjust PID gains, reducing the need for manual intervention and potentially achieving more precise tuning.
4. Model-Based Tuning: This approach involves creating a mathematical model of the system and using it to simulate different tuning scenarios. This can provide insights into how various gain settings will affect system behavior without real-world trial and error.
Challenges in PID Control for Robotics
While PID controllers are powerful, they are not without challenges. Some of the common issues include:
1. Nonlinear Dynamics: Robotic systems often exhibit nonlinear behavior, making it difficult for linear PID controllers to handle effectively.
2. Noise and Disturbances: External disturbances and sensor noise can significantly affect the performance of PID control, especially when derivative gain is involved.
3. Time-Varying Parameters: The dynamic nature of robotic environments means that system parameters can change over time, requiring adaptive or gain-scheduled PID controllers for optimal performance.
4. Coupled Systems: In multi-axis robotics, the interaction between different axes can complicate PID tuning, as changes in one axis can affect others.
Conclusion
Mastering PID control is essential for developing stable and efficient robotic systems. Through careful tuning of the proportional, integral, and derivative gains, engineers can optimize robotic motion, ensuring precise control even in dynamic environments. While challenges such as nonlinear dynamics and external disturbances exist, advancements in tuning methods and adaptive control strategies continue to enhance the robustness of PID-controlled robotic systems. Understanding and leveraging these techniques allows for the creation of robots capable of performing complex tasks with precision and reliability.
Ready to Redefine Your Robotics R&D Workflow?
Whether you're designing next-generation robotic arms, optimizing manipulator kinematics, or mining patent data for innovation insights, Patsnap Eureka, our cutting-edge AI assistant, is built for R&D and IP professionals in high-tech industries, is built to accelerate every step of your journey.
No more getting buried in thousands of documents or wasting time on repetitive technical analysis. Our AI Agent helps R&D and IP teams in high-tech enterprises save hundreds of hours, reduce risk of oversight, and move from concept to prototype faster than ever before.
👉 Experience how AI can revolutionize your robotics innovation cycle. Explore Patsnap Eureka today and see the difference.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com