Introduction

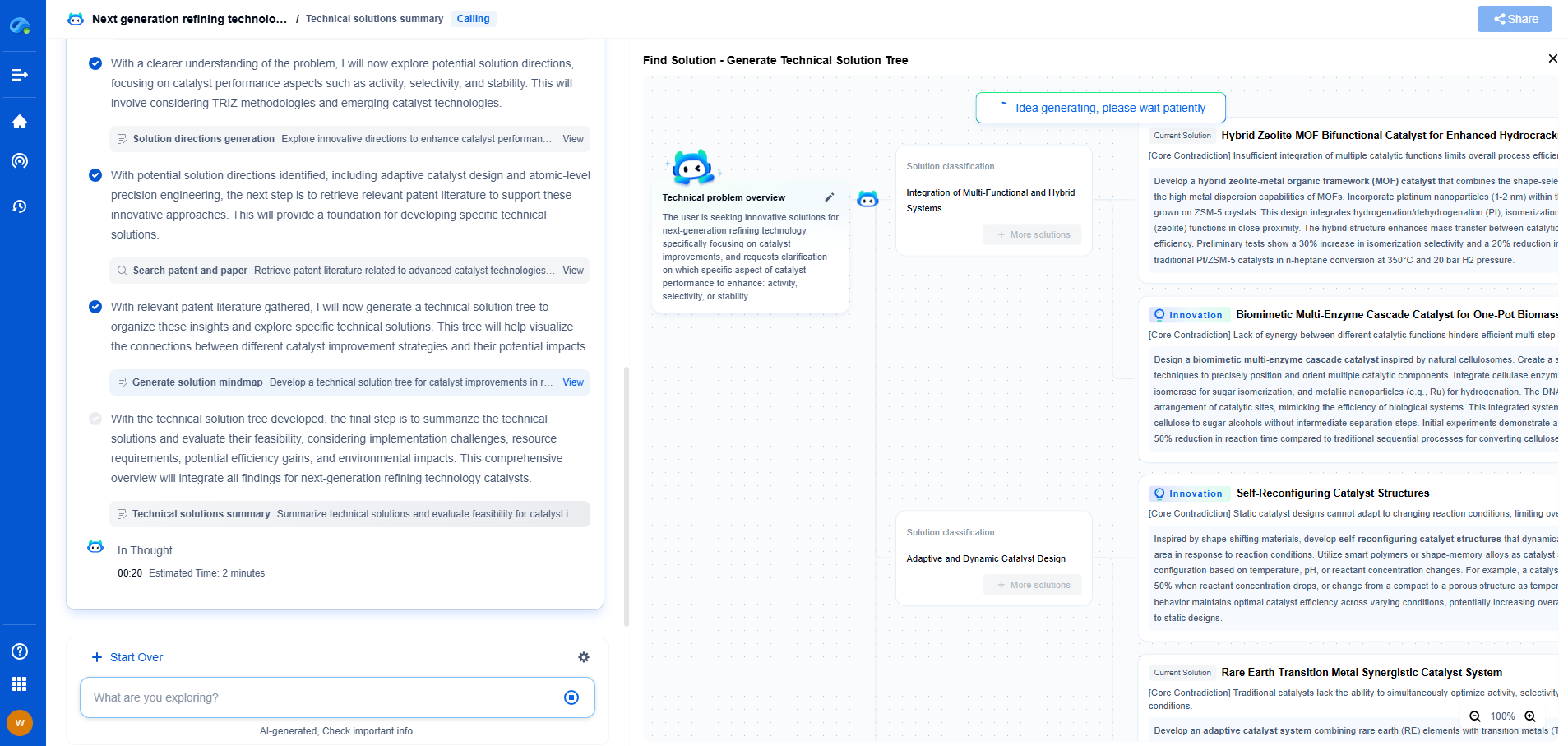
Reinforcement learning (RL) has emerged as a powerful paradigm in artificial intelligence, driven by its ability to solve complex decision-making problems. At its core, reinforcement learning is closely tied to optimal control theory, particularly through the lens of Bellman equations. These equations form the foundation for many RL algorithms and offer a mathematical framework for understanding decision-making processes.

The Relationship Between Reinforcement Learning and Optimal Control

Reinforcement learning and optimal control share a common goal: to determine the best sequence of actions that maximize some notion of cumulative reward or performance. In optimal control, this involves controlling a dynamic system to achieve desired behavior over time. Similarly, in reinforcement learning, an agent interacts with an environment, learning to make decisions that maximize a long-term reward signal.

The connection between these two fields is deeply rooted in the work of Richard Bellman, who introduced the concept of dynamic programming. Bellman's principle of optimality provides a recursive decomposition of complex decision-making processes, allowing for the development of algorithms that can efficiently solve them.

Understanding the Bellman Equations

The Bellman equations are central to the field of reinforcement learning. They provide a recursive relationship for the value functions, which measure the expected cumulative reward an agent can achieve from any given state. There are two primary forms of the Bellman equation: the Bellman expectation equation and the Bellman optimality equation.

1. Bellman Expectation Equation

The Bellman expectation equation defines the relationship for the value function under a specific policy. It expresses the value of a state as the expected reward plus the discounted value of the subsequent state, following the policy:

Vπ(s) = Σaπ(a|s) [R(s, a) + γ Σs' P(s'|s, a) Vπ(s')]

Here, Vπ(s) is the value of state s under policy π, R(s, a) is the reward received after taking action a in state s, P(s'|s, a) is the transition probability to state s' from state s given action a, and γ is the discount factor.

2. Bellman Optimality Equation

The Bellman optimality equation, on the other hand, defines the relationship for the optimal value function, which provides the maximum expected reward that can be achieved from any state. It is given by:

V*(s) = maxa [R(s, a) + γ Σs' P(s'|s, a) V*(s')]

The optimal value function V*(s) represents the best possible outcome from state s, assuming optimal actions are taken.

Revisiting the Bellman Equations in Modern RL

Modern reinforcement learning has seen significant advancements, yet the Bellman equations remain integral to many algorithms. They form the basis of value-based methods like Q-learning and Deep Q-Networks (DQN), where the goal is to estimate the optimal action-value function Q*(s, a) instead of the state value function.

Moreover, policy-based methods, such as Actor-Critic algorithms, also leverage the Bellman equations to enhance policy learning. These methods use the value function to evaluate and improve the policy iteratively, blending the strengths of both value-based and policy-based approaches.

Challenges and Future Directions

Despite their foundational role, the Bellman equations also present challenges. The need for accurate transition models and reward functions can complicate their use in real-world applications. Additionally, the computational cost of solving these equations, especially in high-dimensional spaces, can be prohibitive.

To address these challenges, researchers are exploring various approaches, such as function approximation, model-free methods, and transfer learning. These techniques aim to make reinforcement learning more scalable and applicable to complex environments.

Conclusion

Reinforcement learning, viewed through the lens of optimal control, offers a profound understanding of decision-making processes. The Bellman equations, as revisited in this context, continue to provide a critical framework for designing and analyzing RL algorithms. As the field progresses, building on this foundation will be crucial for developing more efficient and capable reinforcement learning systems that can tackle increasingly complex and dynamic problems.