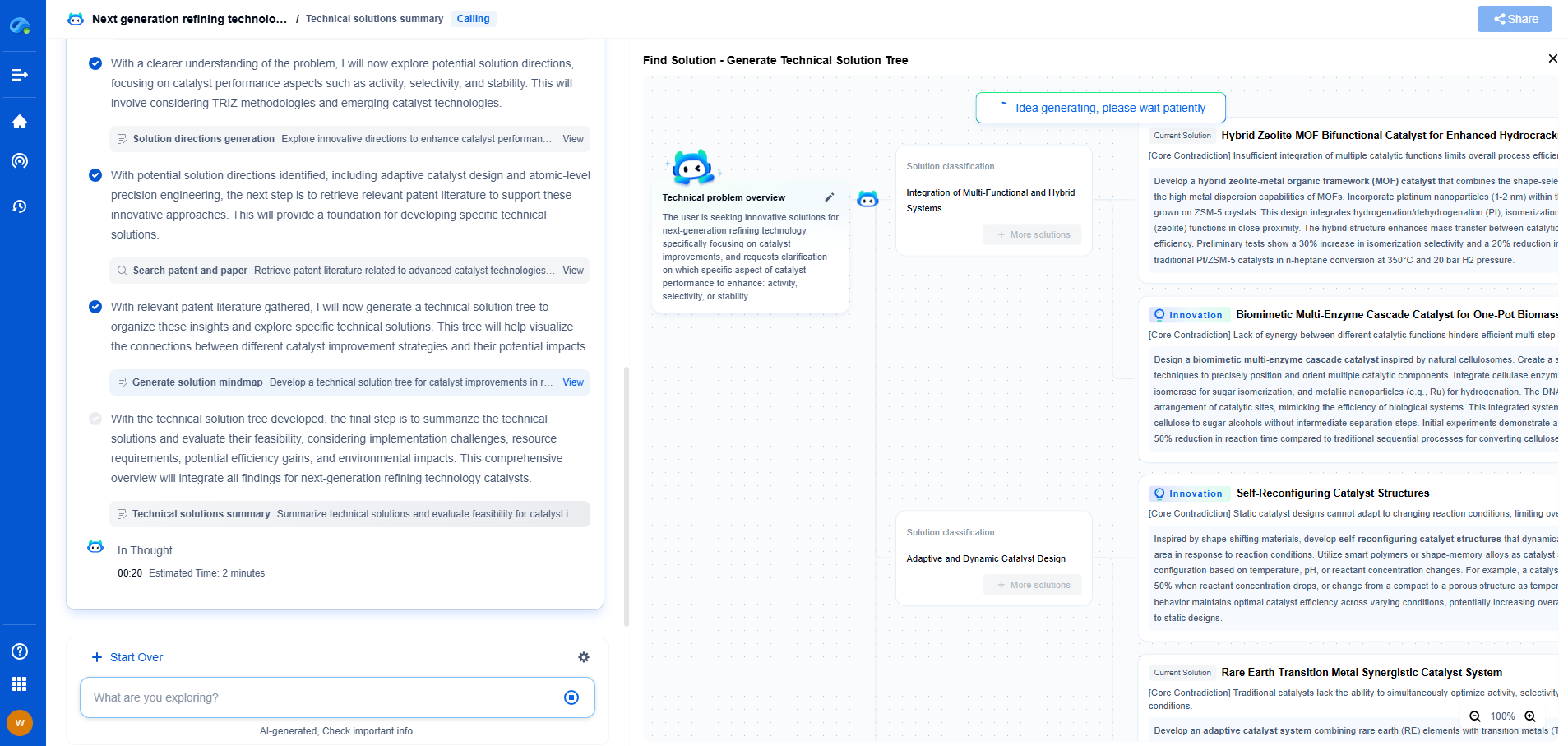
Shannon Entropy vs. Differential Entropy: Discrete vs. Continuous Data in AI
JUN 26, 2025 |
Entropy is a fundamental concept in information theory that measures the uncertainty or unpredictability in a dataset. In the realm of artificial intelligence (AI), entropy is crucial for tasks such as feature selection, decision-making, and understanding data distributions. Two primary forms of entropy are Shannon entropy, suited for discrete data, and differential entropy, applicable to continuous data. Understanding the differences between these types of entropy is essential for effectively leveraging them in AI applications.
Shannon Entropy: A Measure for Discrete Data
Shannon entropy, named after Claude Shannon, the father of information theory, provides a measure of the uncertainty associated with a set of discrete events. It quantifies the expected value of the information contained in a message. In essence, Shannon entropy tells us how much surprise is involved when we observe a particular outcome from a set of possible outcomes.
Mathematically, Shannon entropy is defined as:
H(X) = -Σ p(x) log(p(x)),
where X is a discrete random variable, p(x) is the probability of each possible outcome, and the summation is over all such outcomes. Higher entropy values indicate more unpredictability, while lower values suggest more predictability.
In AI, Shannon entropy is often used in decision tree algorithms to determine the most informative feature for splitting data at each node. By selecting the feature with the highest entropy reduction, the algorithm ensures that each decision contributes to maximizing the information gained, leading to more accurate models.
Differential Entropy: Handling Continuous Data
Differential entropy extends the concept of Shannon entropy to continuous random variables. Unlike discrete variables with distinct probabilities, continuous variables have probability density functions (pdf), necessitating a different approach to measure uncertainty. Differential entropy provides this measure but comes with its own set of challenges and considerations.
Mathematically, differential entropy is defined as:
h(X) = -∫ f(x) log(f(x)) dx,
where X is a continuous random variable, f(x) is its probability density function, and the integration is over the whole range of X. Differential entropy is not invariant under coordinate transformations, meaning it can be affected by changes in scale or shifts in the distribution, unlike Shannon entropy.
In AI, differential entropy is particularly useful in the context of continuous data distributions, such as those found in sensor readings or image data. It can be used to measure the information content of these distributions and help in optimizing models that rely on them.
Comparing Shannon Entropy and Differential Entropy
While both Shannon and differential entropy serve to measure uncertainty, their application domains and interpretations differ significantly. Shannon entropy is straightforward to interpret when dealing with discrete outcomes, making it suitable for categorical data and situations where outcomes can be distinctly enumerated. On the other hand, differential entropy requires careful consideration of the data distribution's scale and shape, as it handles continuous outcomes.
Moreover, the non-invariance of differential entropy under transformation can pose challenges, particularly in comparing entropy values across different datasets or models. This limitation must be addressed by normalizing or standardizing data before applying differential entropy measures.
Applications in AI
Both Shannon and differential entropy find numerous applications in AI. Shannon entropy is commonly used in natural language processing for tasks like language modeling and text classification, where discrete word tokens are the focus. It is also vital in constructing decision trees and random forests by optimizing the selection of splitting criteria.
Differential entropy, on the other hand, is often utilized in domains requiring continuous data analysis. Examples include signal processing, where it helps in compressing audio or image signals, and modeling complex systems in reinforcement learning, where continuous states and actions are prevalent.
Conclusion: Choosing the Right Entropy Measure
When working with AI models, choosing the appropriate entropy measure is crucial for accurately assessing and optimizing data-driven decisions. Shannon entropy provides a reliable framework for discrete data, making it invaluable in scenarios with categorical or finite outcomes. Conversely, differential entropy offers a powerful tool for continuous data, necessitating careful handling of its limitations.
By understanding the distinctions between these entropy forms, AI practitioners can better harness the power of information theory to enhance the performance and interpretability of their models. Both types of entropy offer unique insights into data uncertainty, and leveraging them appropriately can significantly impact the success of AI applications.
Unleash the Full Potential of AI Innovation with Patsnap Eureka
The frontier of machine learning evolves faster than ever—from foundation models and neuromorphic computing to edge AI and self-supervised learning. Whether you're exploring novel architectures, optimizing inference at scale, or tracking patent landscapes in generative AI, staying ahead demands more than human bandwidth.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
👉 Try Patsnap Eureka today to accelerate your journey from ML ideas to IP assets—request a personalized demo or activate your trial now.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com