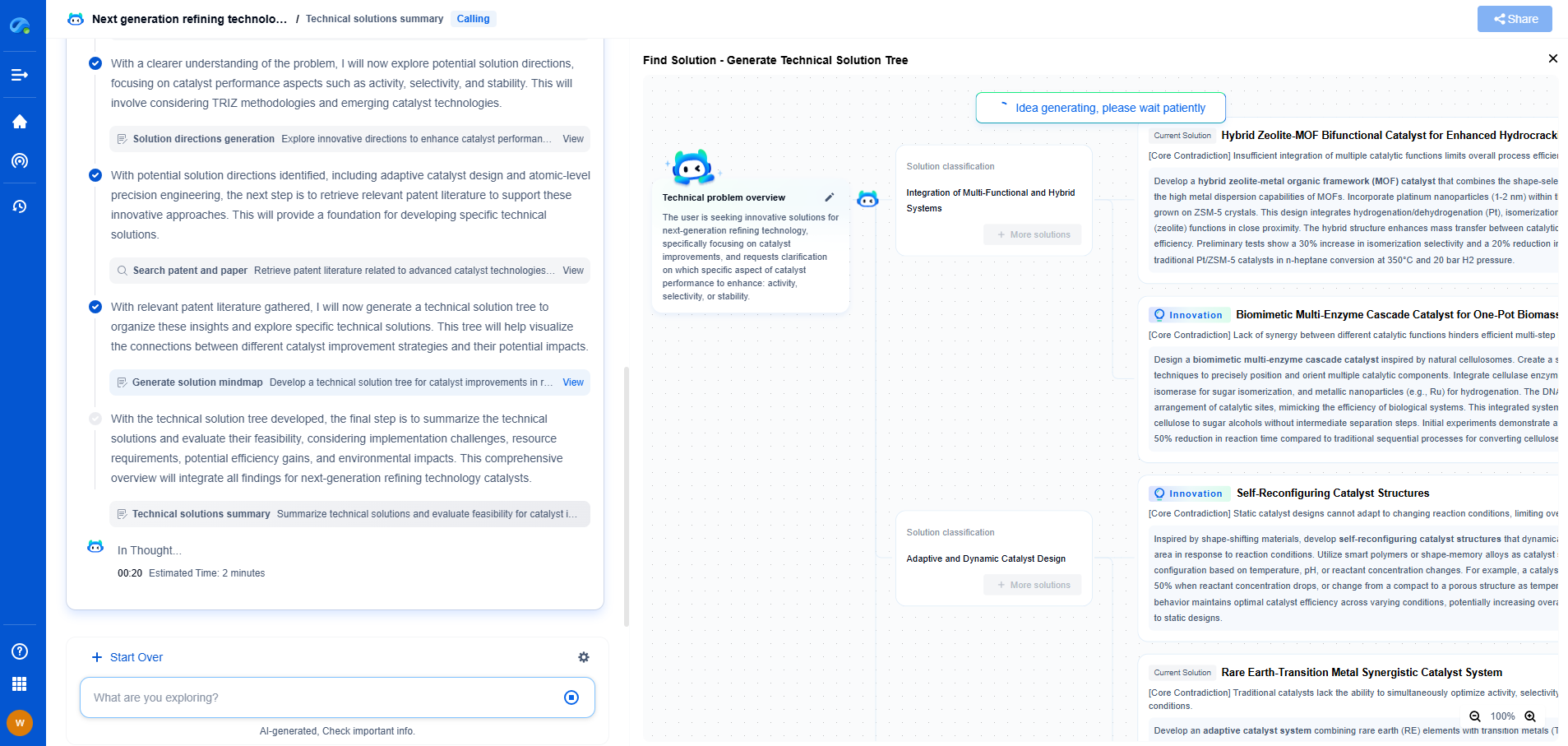
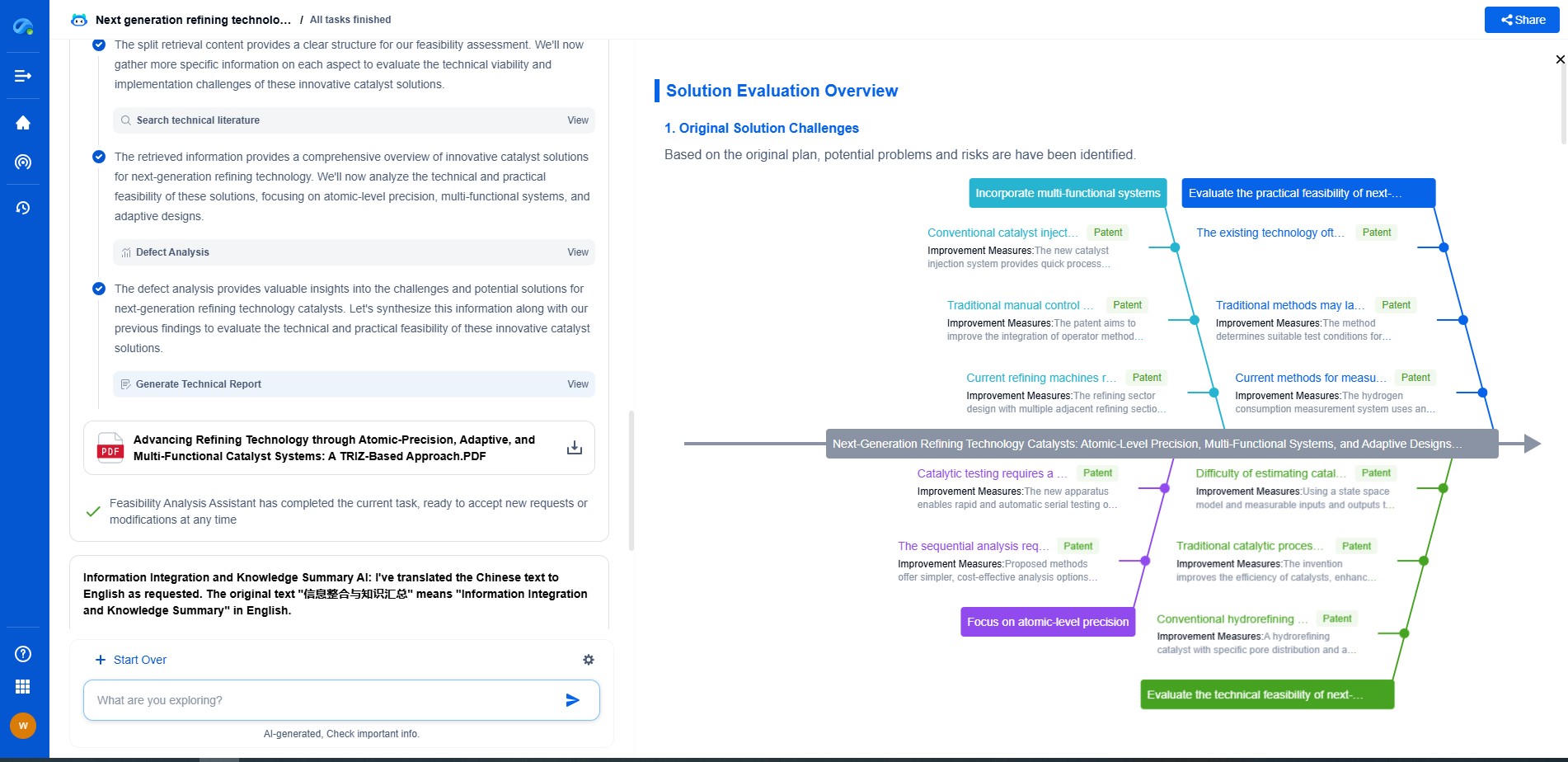
Spherical Joint Kinematics: Euler Angles vs. Quaternions
JUN 26, 2025 |
Spherical joints, often referred to as ball-and-socket joints, are pivotal in both mechanical systems and biological entities. These joints allow for rotational movement around multiple axes, resembling the movement of a ball within a socket. In the realm of kinematics, understanding and describing these movements is essential for applications ranging from robotics to biomechanics. Two primary methods for representing the orientation of these joints are Euler angles and quaternions.
Understanding Euler Angles
Euler angles provide a straightforward method to visualize rotation. Named after the Swiss mathematician Leonhard Euler, this approach represents orientation using three angles. Typically, these angles correspond to rotations around the principal axes—yaw, pitch, and roll. Euler angles are intuitive as they align closely with human perception of orientation and rotation.
However, Euler angles are not without their limitations. One of the most significant issues encountered is known as gimbal lock. Gimbal lock occurs when two of the three rotational axes align, resulting in a loss of one degree of freedom. This can result in erratic behavior in systems relying on Euler angles for orientation control. Additionally, the representation can become ambiguous, as different sets of angles can describe the same orientation.
Exploring Quaternions
Quaternions offer a robust alternative to Euler angles. Developed by mathematician William Rowan Hamilton, quaternions extend complex numbers to higher dimensions. They consist of one real part and three imaginary parts, which can collectively define a rotation in three-dimensional space. Unlike Euler angles, quaternions do not suffer from gimbal lock, making them particularly attractive for applications requiring smooth and continuous rotations.
Quaternions might initially seem less intuitive than Euler angles, but they provide several advantages. They allow for smooth interpolation between orientations (slerp, or spherical linear interpolation), which is invaluable for animating smooth transitions in graphics and robotics. Moreover, quaternions are computationally efficient, with operations like normalization and multiplication simple to execute.
Comparison: Euler Angles vs. Quaternions
When comparing these two methods, it becomes clear that the choice largely depends on the specific requirements of the application. Euler angles might be more suitable for scenarios where simplicity and human interpretability are prioritized. They are easier to understand and visualize, which can be advantageous in educational settings and initial design phases.
In contrast, quaternions are often preferred in dynamic systems where smooth and gimbal-lock-free rotations are critical. Robotics, computer graphics, and aerospace engineering frequently employ quaternions due to their stability and efficiency. The ability to avoid gimbal lock and perform efficient interpolation makes quaternions indispensable in these fields.
Practical Applications and Considerations
In the world of robotics, accurate and stable orientation representation is crucial for tasks such as object manipulation and navigation. Quaternions provide the reliability needed for these applications, enabling robots to perform complex maneuvers without the risk of encountering gimbal lock. Similarly, in computer graphics, where realistic animation is key, quaternions ensure smooth transitions and rotations, enhancing the visual experience.
However, it's essential for practitioners to be aware of potential pitfalls when implementing quaternions. For instance, while quaternions avoid gimbal lock, they can still experience issues if not properly normalized. This can result in drift over time, where the orientation becomes inaccurate. Careful implementation and understanding of their properties are necessary to leverage their full potential.
Conclusion
The choice between Euler angles and quaternions depends on the specific needs of the application at hand. While Euler angles offer simplicity and intuitive understanding, quaternions provide robustness and stability in dynamic environments. Engineers and designers must weigh these factors to select the method that best suits their project's requirements. Both approaches have their merits, and understanding their strengths and limitations is key to successfully navigating the complexities of spherical joint kinematics.
Ready to Redefine Your Robotics R&D Workflow?
Whether you're designing next-generation robotic arms, optimizing manipulator kinematics, or mining patent data for innovation insights, Patsnap Eureka, our cutting-edge AI assistant, is built for R&D and IP professionals in high-tech industries, is built to accelerate every step of your journey.
No more getting buried in thousands of documents or wasting time on repetitive technical analysis. Our AI Agent helps R&D and IP teams in high-tech enterprises save hundreds of hours, reduce risk of oversight, and move from concept to prototype faster than ever before.
👉 Experience how AI can revolutionize your robotics innovation cycle. Explore Patsnap Eureka today and see the difference.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com