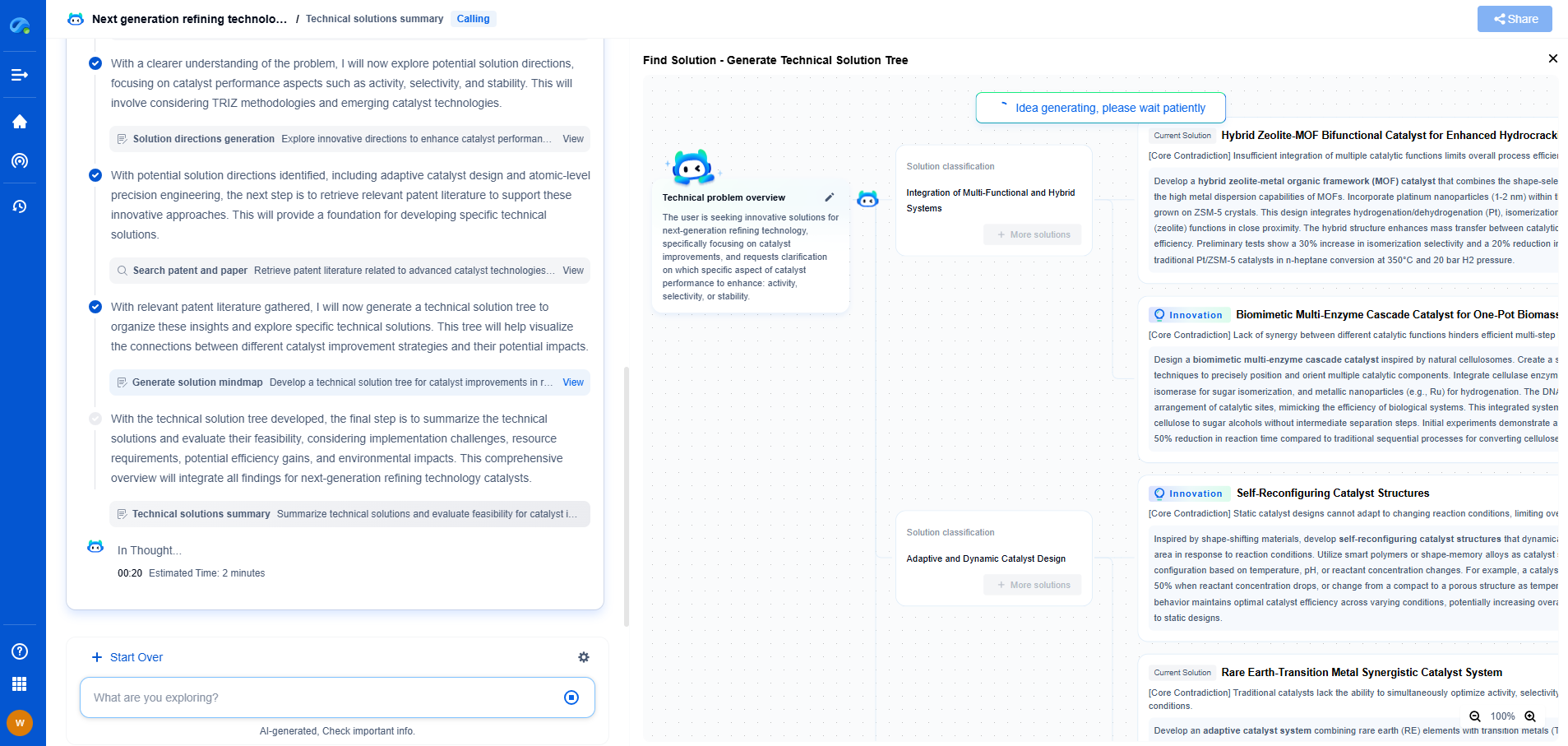
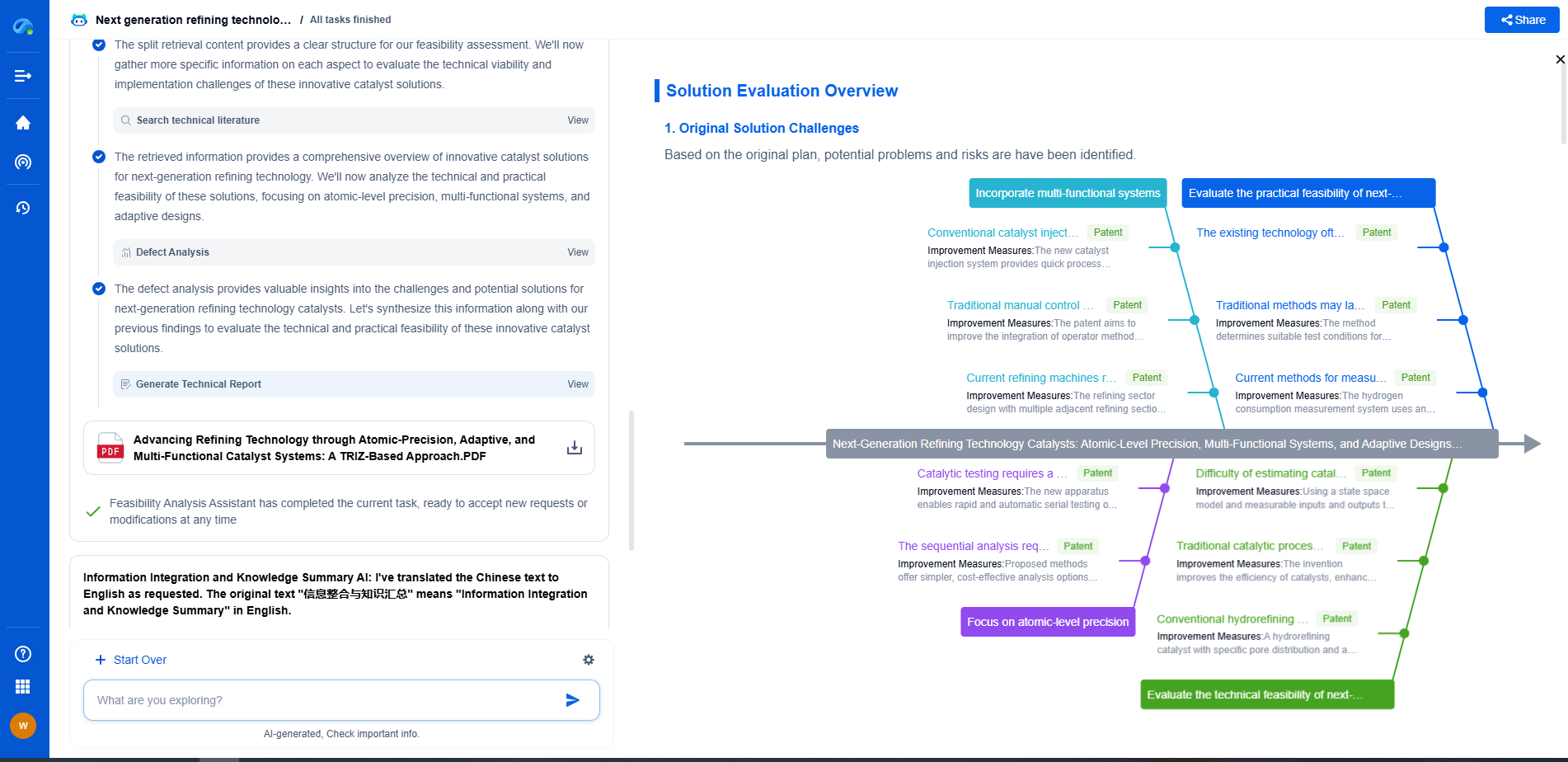
The Math Behind FIR and IIR Filters: What Engineers Should Know
JUL 17, 2025 |
Digital filters are indispensable tools in signal processing, playing a pivotal role in the manipulation of discrete-time signals. The two primary types of digital filters that engineers often work with are FIR (Finite Impulse Response) and IIR (Infinite Impulse Response) filters. Understanding the mathematical foundations of these filters is crucial for designing efficient and effective signal processing systems.
Finite Impulse Response (FIR) Filters
FIR filters are characterized by their finite duration of response to an impulse input. In layman's terms, after a given period, the output of an FIR filter stabilizes to zero. This property is due to the filter’s impulse response being non-zero only over a finite number of samples.
The mathematical backbone of an FIR filter is its difference equation, which can be represented as follows:
y[n] = b0*x[n] + b1*x[n-1] + ... + bN*x[n-N]
In this equation, y[n] is the output signal, x[n] is the input signal, and b0, b1,..., bN are the filter coefficients. The number of coefficients determines the order of the filter, influencing both its complexity and performance. The design of an FIR filter revolves around determining these coefficients in a way that meets specific signal processing criteria, such as frequency response, phase characteristics, and filter stability.
One of the key advantages of FIR filters is their inherent stability. Since they do not rely on feedback from the output, there is no risk of the filter becoming unstable. Additionally, FIR filters can be designed to have a linear phase response, which is highly desirable in many applications as it preserves the wave shape of the filtered signals.
Infinite Impulse Response (IIR) Filters
In contrast to FIR filters, IIR filters can have an impulse response that extends indefinitely. This is because IIR filters incorporate feedback, meaning that past output values influence the current output. The difference equation for an IIR filter is expressed as:
y[n] = a1*y[n-1] + a2*y[n-2] + ... + aM*y[n-M] + b0*x[n] + b1*x[n-1] + ... + bN*x[n-N]
In this formulation, the coefficients a1, a2,..., aM represent the feedback path, while b0, b1,..., bN pertain to the feedforward path. The presence of feedback allows IIR filters to achieve a desired frequency response with a lower filter order compared to FIR filters, which can be advantageous in terms of computational efficiency.
However, the feedback mechanism also introduces potential for instability if the filter coefficients are not chosen carefully. Engineers must ensure that the poles of the IIR filter's transfer function lie within the unit circle in the complex plane to guarantee stability. This requirement adds a layer of complexity to IIR filter design, but the potential for reduced computational load often justifies the effort.
Comparative Analysis: FIR vs. IIR Filters
When choosing between FIR and IIR filters, engineers must weigh several factors. FIR filters, with their inherent stability and linear phase capabilities, are often preferred in applications where these characteristics are critical, such as in data communications and audio processing. The trade-off is the typically higher computational cost associated with FIR filters, especially for achieving sharp cutoff frequencies.
On the other hand, IIR filters are valued for their efficiency in achieving similar frequency responses with lower filter orders. This makes them suitable for real-time applications where computational resources are limited. However, careful attention to stability and phase distortion is necessary when implementing IIR filters.
Practical Considerations in Filter Design
The choice between FIR and IIR filters is not solely dictated by the mathematical properties of the filters themselves. Practical considerations such as available processing power, latency requirements, and the specific characteristics of the signal being processed also play a vital role.
For instance, in an application where phase linearity is paramount, such as in audio signal processing, an FIR filter might be the optimal choice despite its computational demands. Conversely, in real-time systems with stringent latency constraints, the efficiency of an IIR filter might outweigh the challenges associated with ensuring stability.
Conclusion
The math behind FIR and IIR filters is fundamental to understanding their behavior and capabilities. By grasping the underlying principles of these filters, engineers are better equipped to select and design filter solutions that meet the specific needs of their applications. Whether prioritizing stability, phase linearity, or computational efficiency, the choice between FIR and IIR filters should be guided by both mathematical insight and practical considerations.
Whether you’re developing multifunctional DAQ platforms, programmable calibration benches, or integrated sensor measurement suites, the ability to track emerging patents, understand competitor strategies, and uncover untapped technology spaces is critical.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
🧪 Let Eureka be your digital research assistant—streamlining your technical search across disciplines and giving you the clarity to lead confidently. Experience it today.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com