Introduction to Linear Quadratic Regulator (LQR)

Linear Quadratic Regulator (LQR) is a cornerstone of optimal control theory, widely used in engineering and robotics. It offers a systematic way to design controllers that balance performance with cost, ensuring the system behaves optimally in terms of a predefined quadratic cost function. Understanding the math behind LQR is crucial for implementing efficient control strategies in complex systems.

Understanding the Cost Function

At the heart of LQR is the quadratic cost function, which quantifies the trade-offs between state deviations and control efforts. Mathematically, this cost function is expressed as:

J = ∫ (x^T Q x + u^T R u) dt

Here, x is the state vector, u is the control input, Q is a positive semi-definite matrix, and R is a positive definite matrix. These matrices define how much we penalize state deviations and control effort, respectively. The goal of LQR is to minimize this cost function over time.

Dynamic System Representation

Before deriving the control law, it's essential to define the system dynamics. LQR typically deals with linear time-invariant (LTI) systems, represented in state-space form:

x_dot = Ax + Bu

In this equation, x represents the state vector, u denotes the control input, A is the state matrix, and B is the input matrix. These matrices capture the dynamics of the system and how the states evolve over time with respect to the control input.

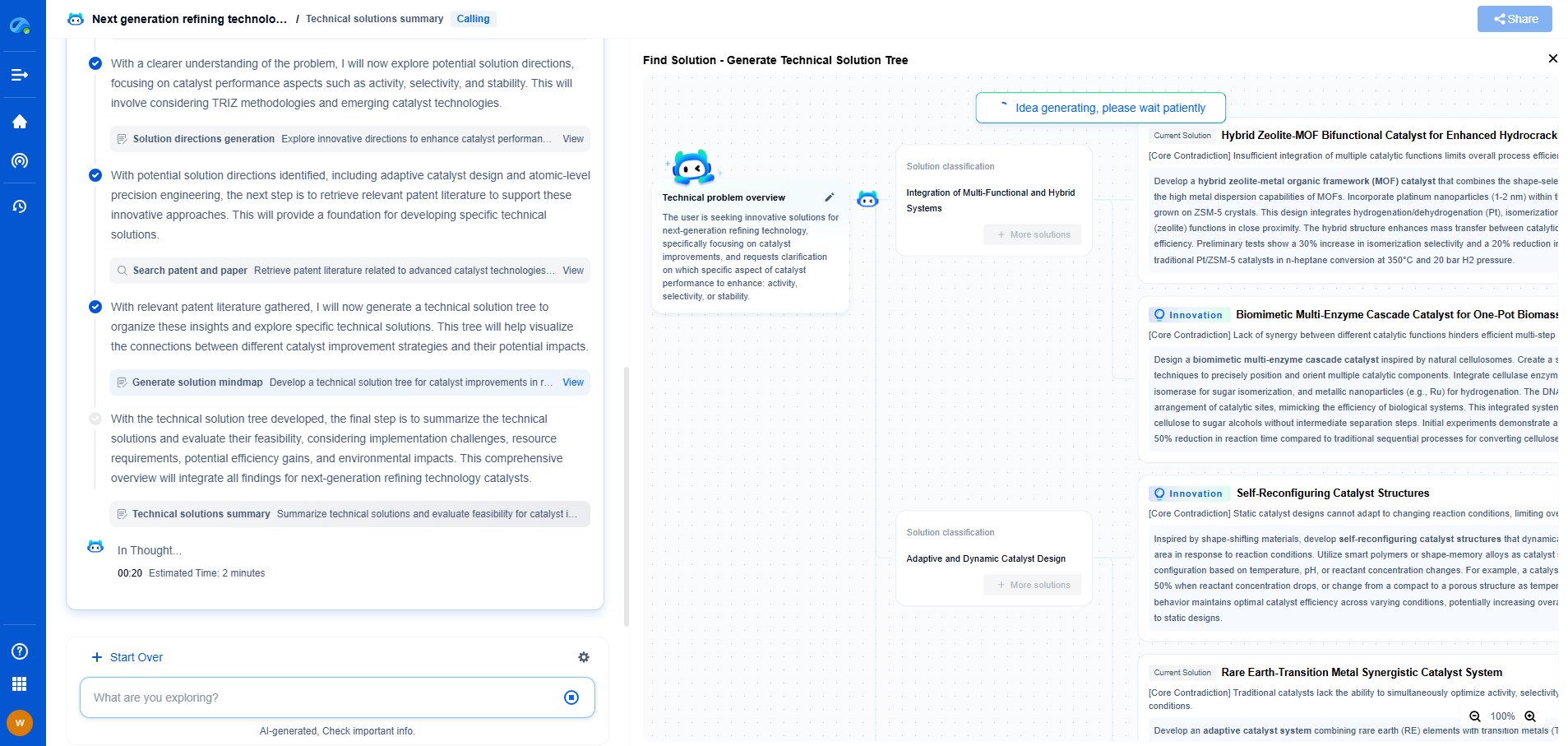
Deriving the Optimal Control Law

To derive the optimal control law, we need to solve the Hamilton-Jacobi-Bellman (HJB) equation, which arises from applying dynamic programming principles to the cost function. This equation involves the cost-to-go function, V(x), and is expressed as:

V(x) = min(∫(x^T Q x + u^T R u + V(x_dot)) dt)

The solution to the HJB equation is facilitated by assuming a quadratic form for V(x):

V(x) = x^T P x

Where P is a symmetric positive definite matrix. Substituting this into the HJB equation leads to a Riccati differential equation:

P_dot = -Q - P A - A^T P + P B R^(-1) B^T P

The challenge is solving this Riccati equation to find the matrix P, which ultimately enables us to express the optimal control law as:

u = -R^(-1) B^T P x

This equation defines the control input u that minimizes the quadratic cost function, steering the system towards optimal performance.

Solving the Riccati Equation

To find the optimal matrix P, we need to solve the Riccati equation. For finite horizon problems, numerical integration techniques are typically employed. However, in infinite horizon problems, the equation becomes algebraic, and P can be found using iterative numerical methods or software packages that implement these solutions.

Applications of LQR

LQR has widespread applications in fields like aerospace engineering, automotive systems, and robotics. It is used for designing controllers in flight systems, optimizing fuel consumption in vehicles, and stabilizing robotic arms. The versatility and reliability of LQR make it a preferred method in scenarios where precision and efficiency are paramount.

Conclusion

The Linear Quadratic Regulator exemplifies the power of mathematical rigor in control theory, providing a robust framework for optimizing system behavior. Understanding the derivation of the LQR control law is essential for engineers and researchers aiming to harness its potential in real-world applications. As technology continues to evolve, the principles behind LQR will undoubtedly remain a fundamental component in the toolkit of control system design.