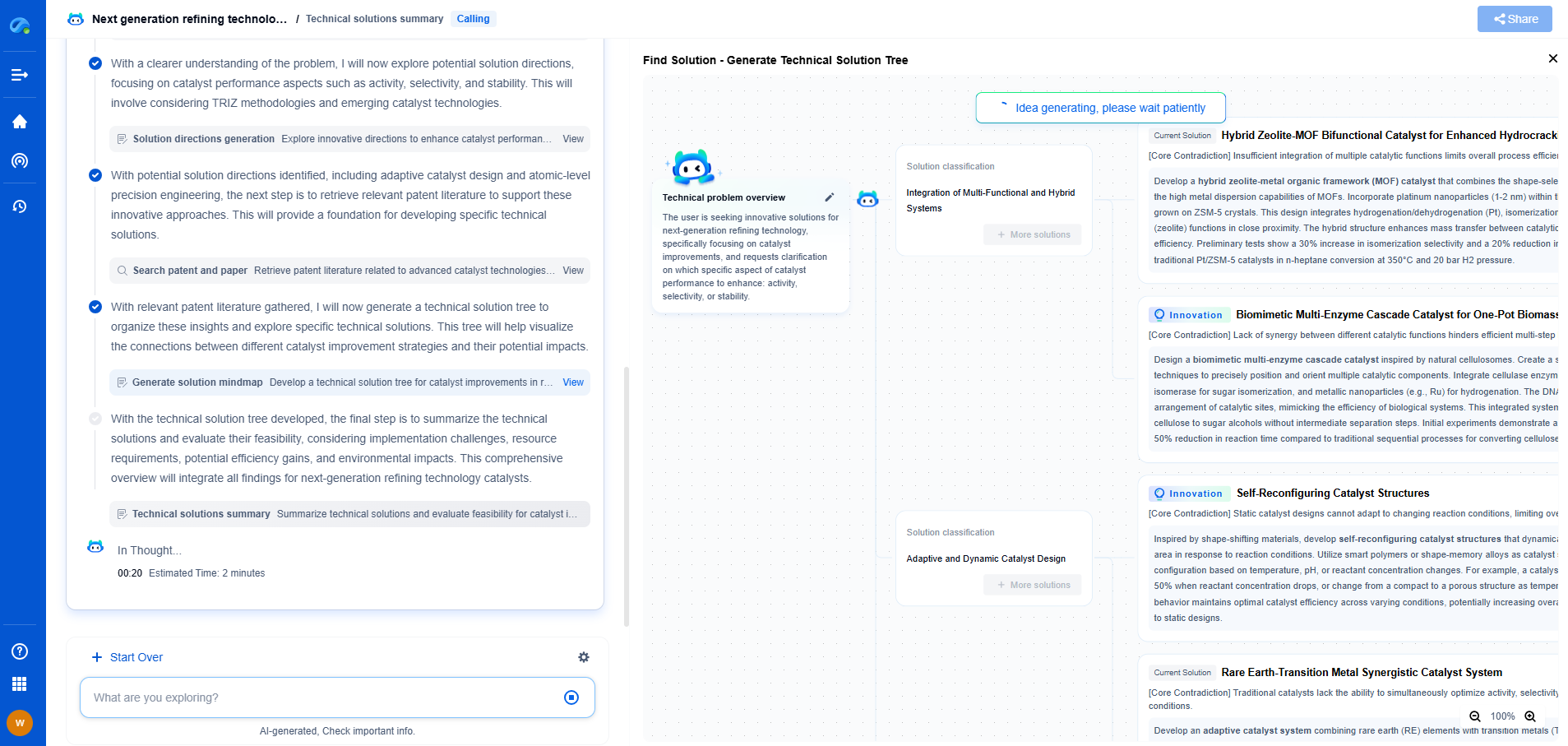
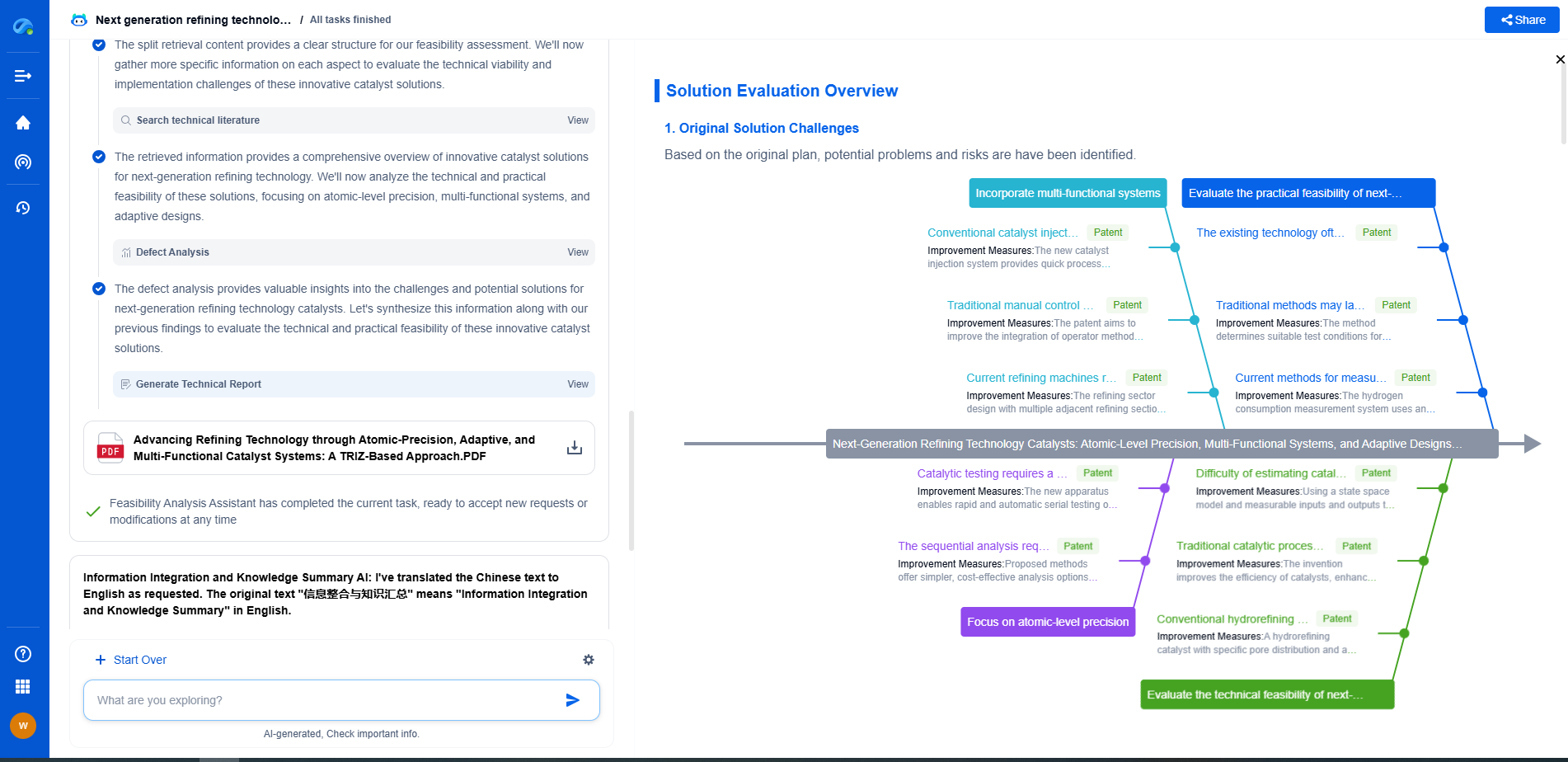
The Mathematics Behind CRC Polynomial Selection
JUL 14, 2025 |
Cyclic Redundancy Check (CRC) is a popular error-detecting code used in digital networks and storage devices to detect accidental changes to raw data. The choice of polynomial plays a crucial role in the efficiency and reliability of CRCs. In this blog, we delve into the mathematics behind CRC polynomial selection, exploring the factors influencing this critical decision and the implications for data integrity.
Understanding CRC Basics
Before we dive into polynomial selection, it’s important to understand how CRCs work. A CRC is generated by dividing the message by a fixed divisor, which is a polynomial, and the remainder of this division is the CRC. Both the message and the divisor are represented as polynomials with binary coefficients. The simplicity of operations in binary arithmetic, coupled with the efficiency of polynomial division, makes CRC a preferred choice in error detection.
The Role of the Polynomial
The polynomial used in CRC calculations acts as a key component of the error detection mechanism. Essentially, it defines the set of detectable errors. The choice of polynomial determines the CRC’s ability to detect errors such as single-bit errors, burst errors, and more. Selecting an optimal polynomial ensures maximum error detection capability while minimizing computational overhead.
Criteria for Polynomial Selection
1. Degree of the Polynomial: The degree of the polynomial is directly related to the length of the CRC. Higher-degree polynomials can detect longer burst errors but increase the size of the CRC, adding to the computational load.
2. Hamming Distance: The Hamming distance of the polynomial affects its ability to detect errors. A polynomial with a higher Hamming distance can detect more types of errors. Common practice is to choose polynomials with a minimum Hamming distance to maximize error detection.
3. Error Detection Capability: The polynomial should be selected based on the types of errors likely to occur in the transmission medium or storage system. For instance, in environments with high noise, a polynomial with robust burst error detection might be necessary.
4. Performance Considerations: The computational efficiency of CRC calculations is crucial, especially in real-time systems. The choice of polynomial should balance between error detection capability and the computational complexity of CRC computation.
Popular CRC Polynomials
Several standard polynomials have proven effective across various applications. For instance, CRC-32 uses the polynomial 0x04C11DB7, which is widely used in Ethernet and ZIP files. This polynomial is efficient in detecting common errors in these environments. Similarly, CRC-16 and CRC-8 are used in different contexts, each optimized for specific error detection needs.
Mathematical Implications
The mathematics behind CRC polynomial selection involves understanding polynomial division and its implications for error detection. The chosen polynomial divides the message, yielding a remainder that helps in identifying any errors in the transmitted data. The polynomial’s properties, such as irreducibility and primitivity, play a significant role in ensuring effective error detection.
An irreducible polynomial cannot be factored into polynomials of smaller degree, making it ideal for detecting errors. Primitivity, on the other hand, ensures that the polynomial can generate a maximum-length sequence, enhancing its ability to detect errors.
Conclusion
The selection of an appropriate CRC polynomial is a critical decision that impacts the effectiveness of error detection in digital communication systems. By understanding the mathematical principles involved, engineers can choose polynomials that offer the best balance between error detection capability and computational efficiency. As technology advances and data transmission continues to grow in complexity, the insights gained from the mathematics of CRC polynomial selection will continue to play a pivotal role in ensuring data integrity.
From 5G NR to SDN and quantum-safe encryption, the digital communication landscape is evolving faster than ever. For R&D teams and IP professionals, tracking protocol shifts, understanding standards like 3GPP and IEEE 802, and monitoring the global patent race are now mission-critical.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
📡 Experience Patsnap Eureka today and unlock next-gen insights into digital communication infrastructure, before your competitors do.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com