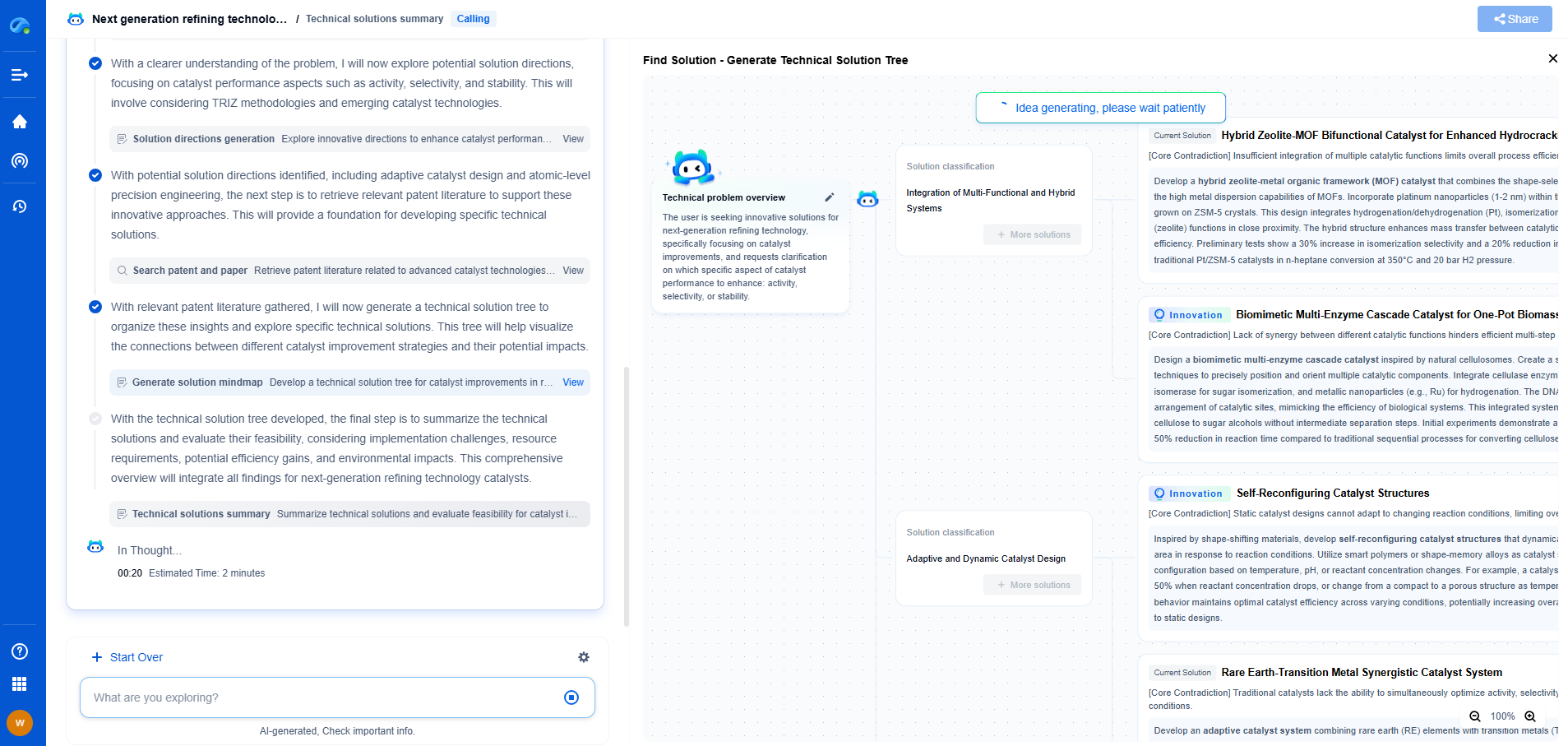
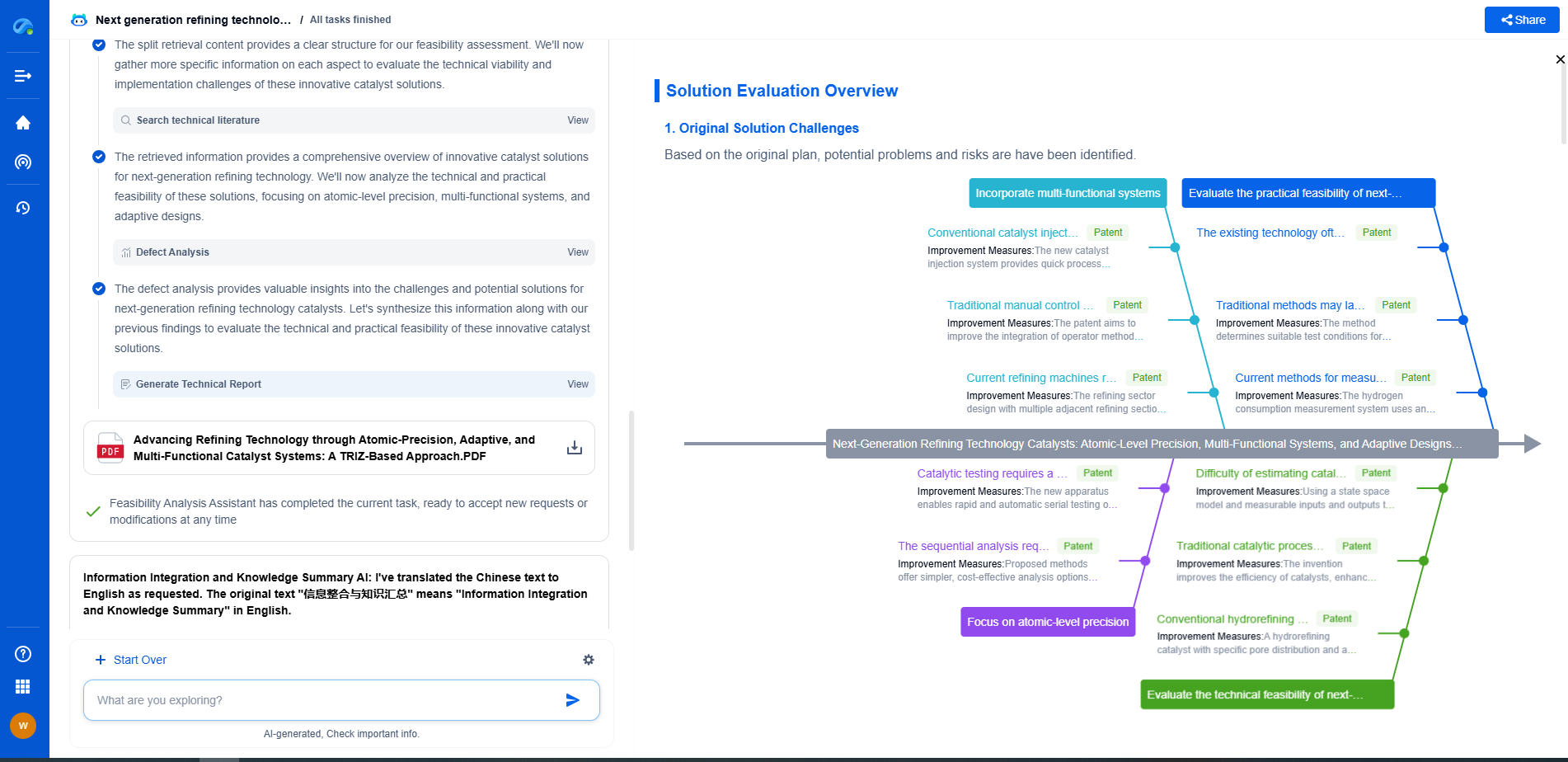
The Mathematics Behind Diffie-Hellman Key Exchange
JUL 14, 2025 |
The realm of cryptography has long been vital to maintaining the confidentiality and security of information. Among the foundational mechanisms is the Diffie-Hellman key exchange, a method that allows two parties to establish a shared secret over an insecure channel. This key exchange is pivotal in encrypted communications, providing the groundwork for secure interactions over the internet.
Understanding the Basics
At the heart of the Diffie-Hellman key exchange is its unique ability to allow two parties to generate a common secret without transmitting it directly. Imagine Alice and Bob, who want to communicate securely. They can use the Diffie-Hellman protocol to generate a shared key, which can then be used to encrypt messages between them.
The process begins with both parties agreeing on a large prime number, p, and a base, g, which is a primitive root modulo of p. These numbers do not need to be kept secret and can be shared openly. Next, Alice selects a private key, a, and Bob selects a private key, b. The security of the protocol is rooted in these private keys, which must be kept confidential.
The Mathematics Behind the Process
The mathematical beauty of the Diffie-Hellman key exchange lies in the use of modular arithmetic. Once Alice and Bob have selected their private keys, they compute their respective public keys. Alice calculates her public key as A = g^a mod p, and Bob calculates his as B = g^b mod p. These public keys are exchanged between Alice and Bob.
The critical step is the computation of the shared secret. Alice uses Bob’s public key and her private key to compute the shared secret as S = B^a mod p. Similarly, Bob uses Alice’s public key and his private key to compute the shared secret as S = A^b mod p. Due to the properties of modular arithmetic, both computations result in the same shared secret, S.
The Security of Diffie-Hellman
The security of the Diffie-Hellman key exchange relies on the difficulty of solving the discrete logarithm problem. Simply put, even though it is easy to compute the public keys from the private keys, it is computationally infeasible to reverse the process and derive the private keys from the public keys. This ensures that even if an attacker intercepts the public keys exchanged between Alice and Bob, they cannot derive the shared secret without solving a problem that is currently considered impractical for large values of p.
Applications and Limitations
The Diffie-Hellman key exchange is widely used in protocols like TLS (Transport Layer Security) to secure internet communications. It forms the backbone of various encryption schemes and ensures that data transmitted over networks remains confidential and intact.
However, it's important to acknowledge the limitations. The traditional Diffie-Hellman key exchange does not provide authentication, meaning that while it secures the communication channel, it does not verify the identities of the communicating parties. This limitation can be addressed by incorporating additional cryptographic techniques, such as digital signatures.
Conclusion
The Diffie-Hellman key exchange is a cornerstone of modern cryptography, offering a secure way to establish a shared secret over an unsecured channel. Its reliance on the principles of modular arithmetic and the discrete logarithm problem ensures that it remains a robust method for key exchange despite its age. As the landscape of cryptography continues to evolve, understanding the mathematics behind key exchange methods like Diffie-Hellman remains crucial for securing digital communications.
From 5G NR to SDN and quantum-safe encryption, the digital communication landscape is evolving faster than ever. For R&D teams and IP professionals, tracking protocol shifts, understanding standards like 3GPP and IEEE 802, and monitoring the global patent race are now mission-critical.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
📡 Experience Patsnap Eureka today and unlock next-gen insights into digital communication infrastructure, before your competitors do.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com