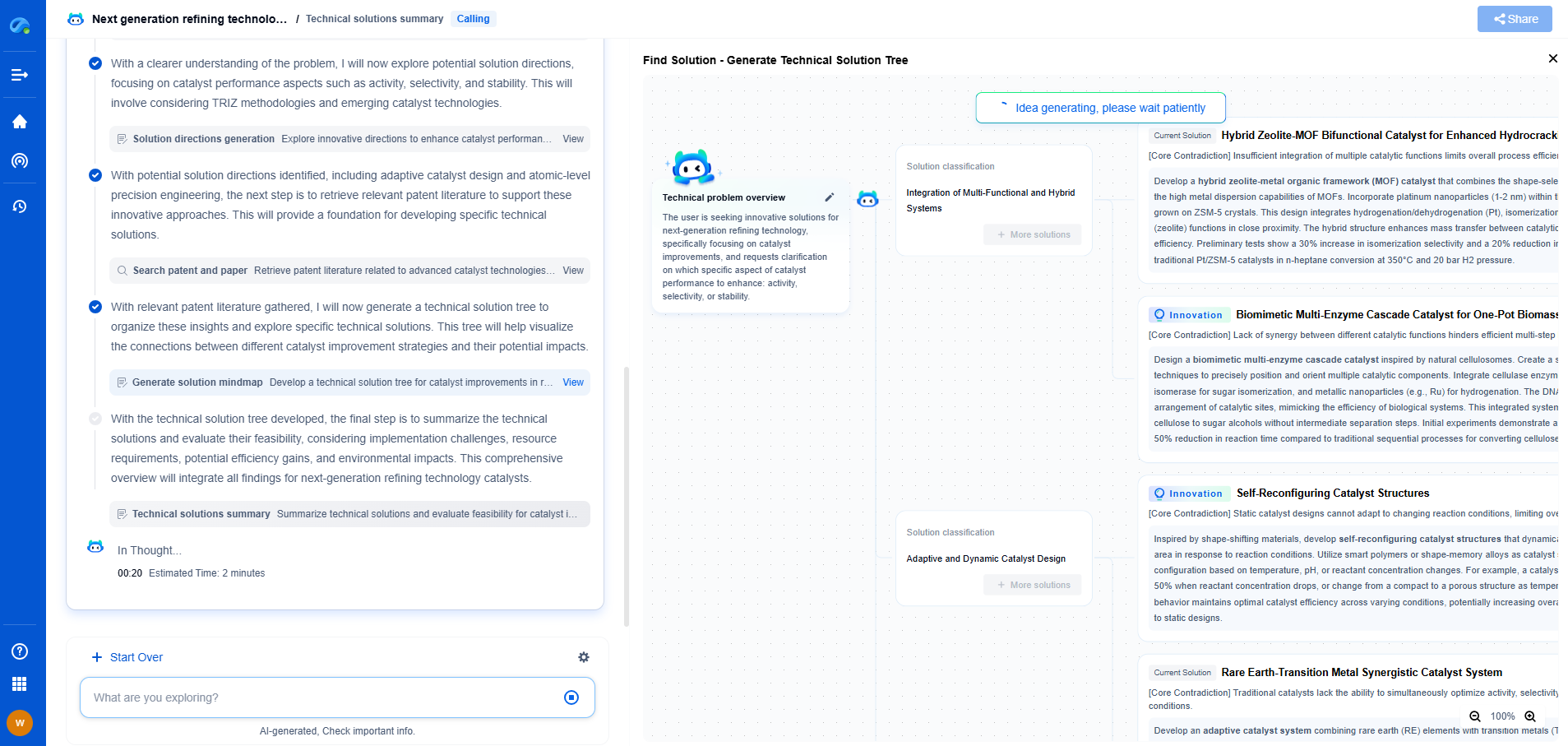
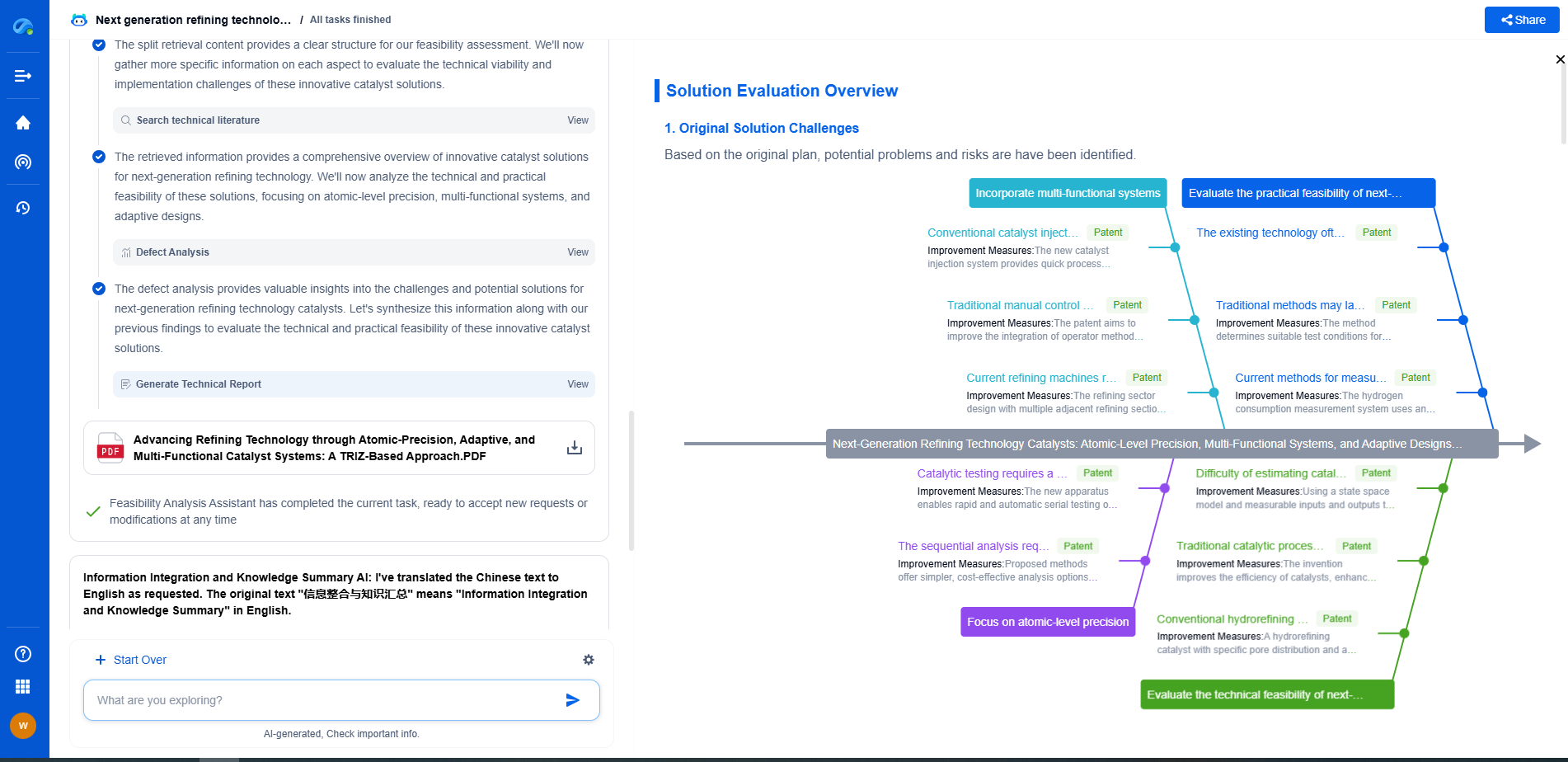
Uncertainty-Aware Metrics: Bayesian Approaches to Model Evaluation
JUL 10, 2025 |
In the rapidly evolving landscape of machine learning and artificial intelligence, models are increasingly deployed in critical applications, from healthcare to autonomous vehicles. As these models take on more substantial roles in decision-making processes, understanding and quantifying their uncertainty becomes crucial. Traditional metrics like accuracy, precision, recall, and F1-score provide valuable insights but often fall short of conveying the full picture, especially in scenarios where uncertainty can significantly impact outcomes. Enter Bayesian approaches to model evaluation, which emphasize uncertainty-aware metrics, offering a more nuanced understanding of model performance.
The Need for Uncertainty-Aware Metrics
Uncertainty is inherent in any predictive model due to factors like data noise, model assumptions, and inherent randomness in the world. Traditional metrics can sometimes mask these uncertainties, leading to overconfident predictions and potentially risky decisions. By incorporating uncertainty into model evaluation, we can better understand the reliability of predictions, identify areas of improvement, and make more informed decisions.
Bayesian approaches offer a robust framework for quantifying and incorporating uncertainty into model performance evaluation. They provide a probabilistic perspective, allowing us to express confidence in predictions with a degree of certainty rather than absolute terms. This perspective is particularly valuable in applications where the cost of errors is high.
Understanding Bayesian Approaches
Bayesian statistics is a paradigm that uses probability distributions to represent uncertainty in model parameters and predictions. Unlike frequentist methods, which provide point estimates, Bayesian methods yield distributions, offering a more comprehensive picture of uncertainty.
In the context of model evaluation, Bayesian approaches involve computing the posterior distribution of model parameters given the observed data. This involves using Bayes' theorem, which updates the prior beliefs about parameters based on the likelihood of the observed data. The result is a posterior distribution that reflects the updated beliefs, incorporating both prior knowledge and observed evidence.
Implementing Bayesian Metrics
Implementing Bayesian metrics often involves several steps. Firstly, we define a prior distribution for the model parameters, representing our initial beliefs before observing the data. Next, we specify a likelihood function that describes how likely the observed data is, given the model parameters. Using Bayes’ theorem, we combine these to obtain the posterior distribution.
From the posterior, we can derive various uncertainty-aware metrics. For instance, instead of estimating a single value for accuracy, we can compute a distribution over possible accuracy values, providing insights into its variability. Similarly, metrics like precision and recall can be expressed as distributions, allowing us to communicate the uncertainty associated with them effectively.
Practical Applications and Benefits
One of the most significant advantages of Bayesian metrics is their ability to convey uncertainty in a manner that is interpretable and actionable. For instance, in medical diagnostics, knowing the confidence interval around a model's prediction can help practitioners assess risk and make more informed decisions.
Moreover, Bayesian approaches facilitate robust model comparison. By comparing posterior distributions instead of point estimates, we can determine the relative strengths and weaknesses of models in a more statistically sound manner. This is particularly useful in model selection and hyperparameter tuning, where uncertainty can guide the selection of more reliable models.
Challenges and Considerations
Despite their advantages, Bayesian approaches come with their own set of challenges. The computational complexity of estimating posterior distributions can be significant, especially for complex models with large datasets. Advanced techniques like Markov Chain Monte Carlo (MCMC) and Variational Inference are often employed to approximate these distributions, but they require careful tuning and expertise.
Additionally, selecting appropriate prior distributions can be challenging, as they can significantly influence the posterior outcomes. It requires domain knowledge and careful consideration to ensure that priors are informative yet not overly biased.
Conclusion
As machine learning models continue to impact critical aspects of our lives, understanding and quantifying their uncertainty becomes increasingly important. Bayesian approaches to model evaluation provide a compelling framework for incorporating uncertainty into performance metrics, offering richer insights and supporting more informed decision-making. While challenges remain, the benefits of uncertainty-aware metrics make them an essential tool in the arsenal of data scientists and model evaluators. Embracing these approaches can lead to more robust, reliable, and trustworthy AI systems that better serve their intended purposes.
Image processing technologies—from semantic segmentation to photorealistic rendering—are driving the next generation of intelligent systems. For IP analysts and innovation scouts, identifying novel ideas before they go mainstream is essential.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
🎯 Try Patsnap Eureka now to explore the next wave of breakthroughs in image processing, before anyone else does.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com