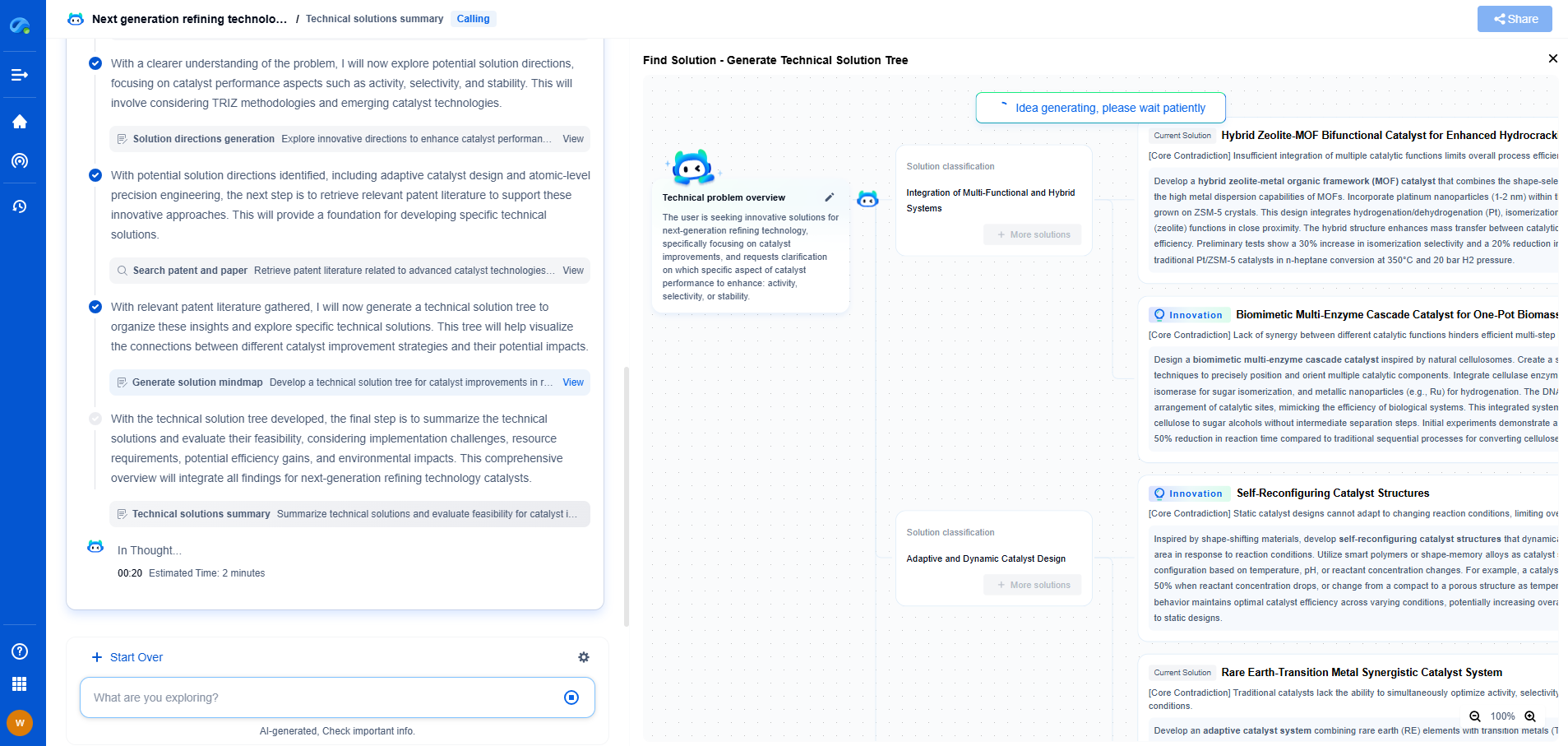
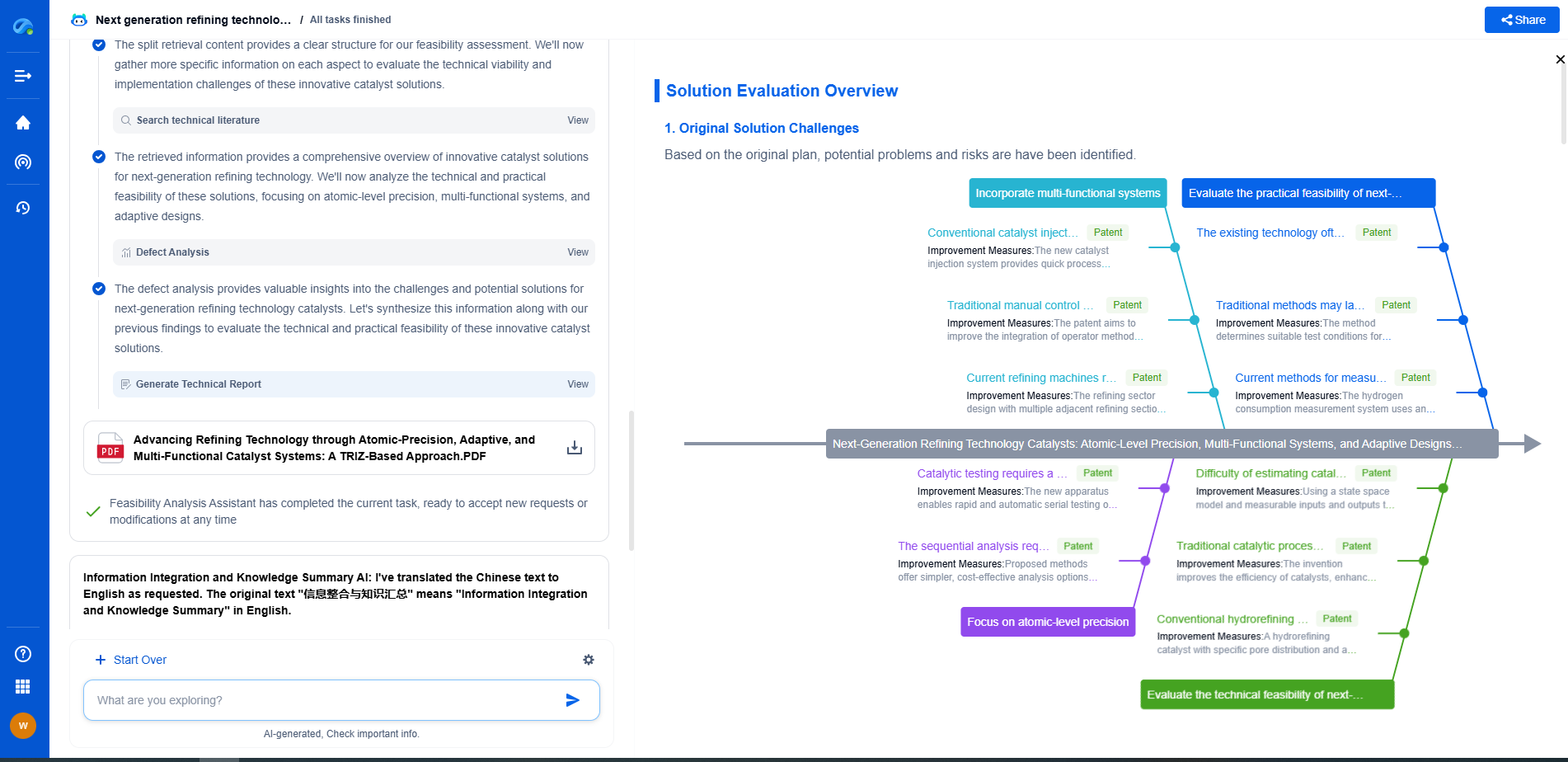
Understanding Allan Variance for Long-Term Stability Assessment
JUL 17, 2025 |
In the realm of precision measurements, particularly in time and frequency domains, understanding the stability of a system over time is crucial. One of the most valuable tools used for assessing long-term stability is Allan variance. This statistical measure helps in analyzing the stability of fluctuating signals and is widely used in fields such as telecommunications, navigation, and instrumentation. Understanding Allan variance can provide insights into the behavior of systems that rely on high precision, such as atomic clocks, gyroscopes, and oscillators.
The Basics of Variance and Stability
Before diving into Allan variance, it's essential to grasp the basic concept of variance in the context of statistical analysis. Variance measures how much a set of numbers is spread out, indicating how much each number in the set deviates from the mean. In systems where stability is key, such as precision timing devices, understanding how these deviations occur over time is crucial. Traditional variance, however, often falls short when dealing with time-varying signals where phase noise and frequency instability come into play.
Allan Variance: A Solution to Traditional Variance Limitations
Allan variance, named after David W. Allan, who introduced it in the 1960s, provides a solution to the limitations of traditional variance in long-term stability assessments. Unlike standard variance, Allan variance is specifically designed to analyze time-dependent fluctuations, making it an ideal tool for quantifying the stability of time and frequency signals over different time intervals.
Allan variance is calculated using a series of overlapping time intervals to measure the deviation of a signal's frequency from its average over varying durations. By examining these deviations, Allan variance can characterize different types of noise, such as white noise, flicker noise, and random walk noise, each of which impacts system stability in distinct ways.
Calculating Allan Variance
To calculate Allan variance, one must first acquire a series of time-stamped frequency measurements of the signal in question. The data is then divided into overlapping time intervals or "bins," and the average frequency for each bin is calculated. The differences between consecutive averages are squared, summed, and then averaged over the total number of intervals. This results in the Allan variance, which is expressed as a function of the length of the time interval used.
Plotting Allan variance against various time intervals on a log-log scale yields an Allan deviation plot, providing a clear visual representation of the system's stability and noise characteristics over time. The slope of different sections of this plot can indicate the dominant type of noise present in the system, allowing for targeted improvements in design and performance.
Applications in Real-World Systems
Allan variance is a critical tool in fields where high precision and long-term stability are paramount. In telecommunications, for instance, maintaining stable frequency references is vital for synchronizing networks and ensuring data integrity. Allan variance helps in identifying and mitigating sources of instability, thereby enhancing the reliability of communication systems.
In navigation, especially in systems like GPS, Allan variance aids in assessing the stability of oscillators used in satellite clocks, which is crucial for accurate positioning. Similarly, in scientific instrumentation, where precise timekeeping is essential, Allan variance assists in evaluating the performance of atomic clocks and other time-keeping devices, ensuring they meet the stringent requirements of modern applications.
Conclusion: The Importance of Allan Variance
The significance of Allan variance in assessing long-term stability cannot be overstated. By providing a nuanced understanding of how signals behave over time, it allows researchers and engineers to pinpoint sources of instability and develop solutions to enhance system performance. As technology advances and the demand for precision continues to grow, Allan variance will remain an indispensable tool in the quest for reliability and accuracy in various high-stakes applications. Understanding and leveraging this powerful statistical method is essential for anyone involved in fields where stability and precision are critical.
Whether you’re developing multifunctional DAQ platforms, programmable calibration benches, or integrated sensor measurement suites, the ability to track emerging patents, understand competitor strategies, and uncover untapped technology spaces is critical.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
🧪 Let Eureka be your digital research assistant—streamlining your technical search across disciplines and giving you the clarity to lead confidently. Experience it today.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com