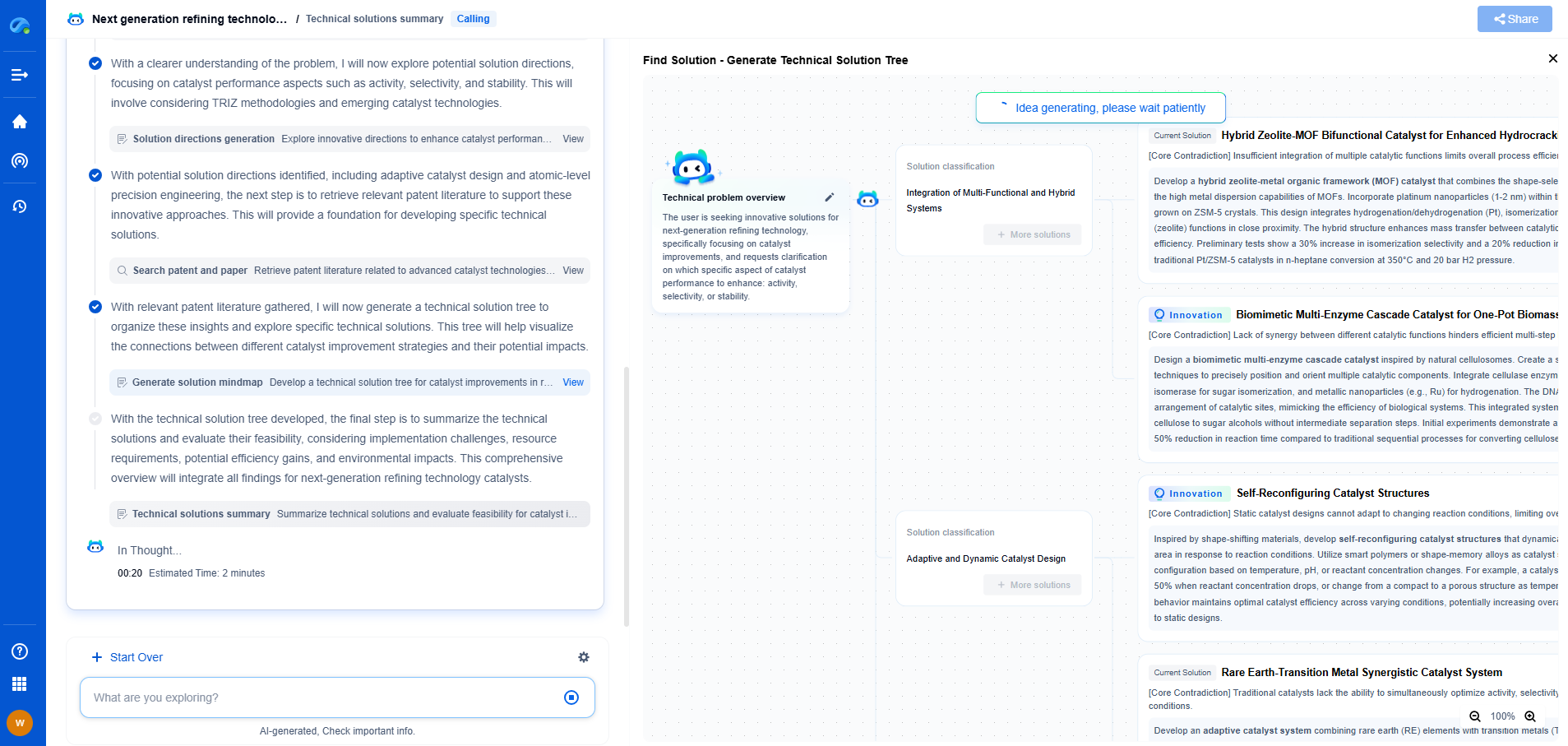
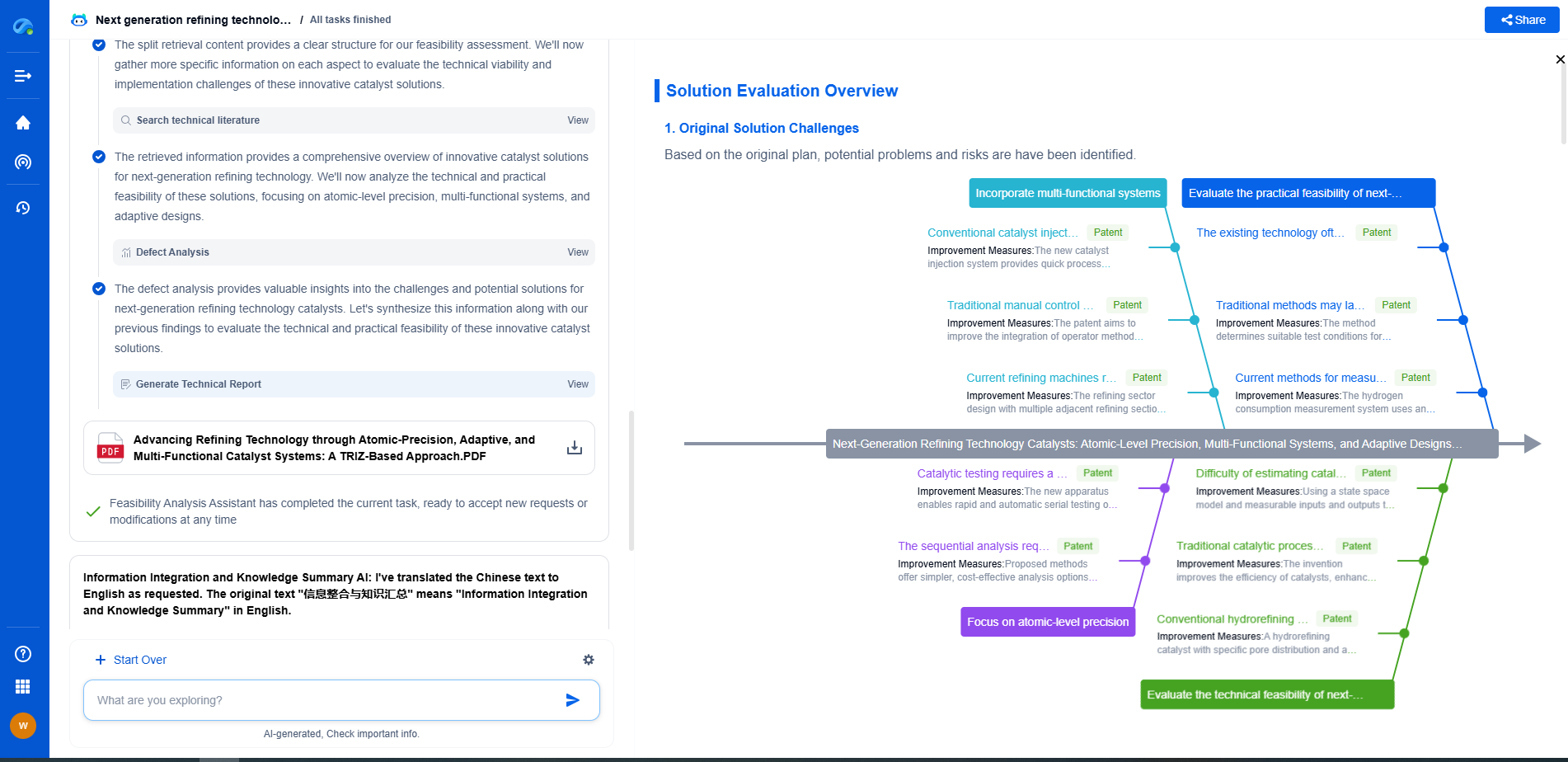
Understanding Hamming code: How it corrects single-bit errors
JUL 14, 2025 |
Error detection and correction are critical aspects of digital communication systems. As data is transmitted over various channels, it is susceptible to noise and interference, which can lead to errors. One effective method to handle such errors is the Hamming code, a technique devised by Richard Hamming in 1950. This ingenious method not only detects errors but also corrects single-bit errors, thereby ensuring data integrity during transmission. In this article, we will delve into the workings of the Hamming code, explore its ability to correct single-bit errors, and understand its implementation.
Understanding Error Detection and Correction
Before diving into Hamming code, it's essential to grasp the basics of error detection and correction. In any communication system, data is represented in binary form, consisting of bits (0s and 1s). Errors occur when bits are altered during transmission due to interference or other factors. Error detection involves identifying these incorrect bits, while error correction goes a step further by restoring the original data. Different techniques have been developed over time, with the Hamming code being one of the most efficient for correcting single-bit errors.
The Structure of Hamming Code
Hamming code is a type of linear error-correcting code that uses redundant bits to establish and maintain error correction. In a typical Hamming code scheme, the data bits are interspersed with parity bits. These parity bits are strategically placed to detect and correct errors. The position and the number of these bits depend on the length of the data.
To determine the number of parity bits required, the following formula is used:
2^r >= m + r + 1
where 'r' is the number of parity bits and 'm' is the number of data bits. The parity bits are placed at positions that are powers of 2 (1, 2, 4, 8, etc.). The remaining positions are filled with data bits.
How Hamming Code Corrects Single-Bit Errors
The power of Hamming code lies in its ability to correct single-bit errors. Once the parity bits are set, they form a pattern that can be used to identify any errors in the received data. By recalculating the parity bits on the receiver's end and comparing them to those in the received message, it is possible to pinpoint the erroneous bit.
Here's a step-by-step process of how Hamming code corrects errors:
1. Calculate Parity Bits: When encoding data, parity bits are computed using specific combinations of data bits. Each parity bit checks a unique set of data bits, according to its position.
2. Transmit the Data: The encoded message containing both data and parity bits is sent over the channel.
3. Receive and Compare: The receiver recalculates the parity bits from the received message.
4. Error Detection: If the recalculated parity bits differ from the received parity bits, it indicates an error. The specific combination of mismatch indicates the position of the erroneous bit.
5. Error Correction: By observing the calculated discrepancy, the exact position of the bit error can be identified. Since the error is a single-bit error, flipping the identified bit will correct the data.
Practical Application of Hamming Code
Hamming code is widely used in computer memory systems, data transmission, and error detection protocols due to its simplicity and efficiency. Its ability to detect and correct single-bit errors makes it a practical choice in scenarios where data reliability is paramount. For example, in memory storage systems, Hamming code ensures that data can be corrected in the event of a single-bit error, thus maintaining system reliability.
Limitations and Considerations
While Hamming code is effective for single-bit error correction, it has limitations in handling multiple errors. If two or more bits are altered during transmission, Hamming code may misinterpret or fail to correct the errors. Therefore, for environments prone to multiple bit errors, more advanced error correction methods such as Reed-Solomon or Turbo codes may be utilized.
Conclusion
Hamming code remains a fundamental tool in the field of error correction, offering a reliable method for identifying and rectifying single-bit errors. Its legacy continues in modern communication systems, providing a robust framework for maintaining data integrity. Understanding the mechanics behind Hamming code not only highlights its importance but also underscores the evolution of error correction techniques in safeguarding digital communication. As technology advances, the principles of Hamming code continue to inspire more complex and efficient error-correcting algorithms, ensuring that the data we rely on remains accurate and trustworthy.
From 5G NR to SDN and quantum-safe encryption, the digital communication landscape is evolving faster than ever. For R&D teams and IP professionals, tracking protocol shifts, understanding standards like 3GPP and IEEE 802, and monitoring the global patent race are now mission-critical.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
📡 Experience Patsnap Eureka today and unlock next-gen insights into digital communication infrastructure, before your competitors do.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com