Understanding the transient response in electronic circuits is paramount for engineers and hobbyists who design and analyze circuits. This aspect of circuit behavior reveals how an electronic circuit responds to changes in input, particularly during the transition from one steady state to another. Delving into this topic requires a look at concepts, equations, and applications that make transient response a cornerstone of circuit analysis.

Introduction to Transient Response

Transient response refers to how a circuit reacts to a change, such as a sudden application or removal of power. It is a temporary response that eventually settles down to a steady-state condition. Understanding this behavior is crucial as it affects the functionality and stability of electronic devices. For instance, when a circuit is turned on, its components do not instantly reach their operating conditions. Instead, they undergo a transient phase before achieving a steady state.

The Nature of Transient Responses

The transient response of a circuit is characterized by how voltages and currents change over time. It can be observed in various forms such as exponentially rising or decaying waveforms. This behavior is primarily influenced by the reactive components in the circuit—capacitors and inductors—which store and release energy over time. These components cause the circuit to respond with a time-dependent behavior when subjected to a step input or any other type of excitation.

Mathematical Modeling

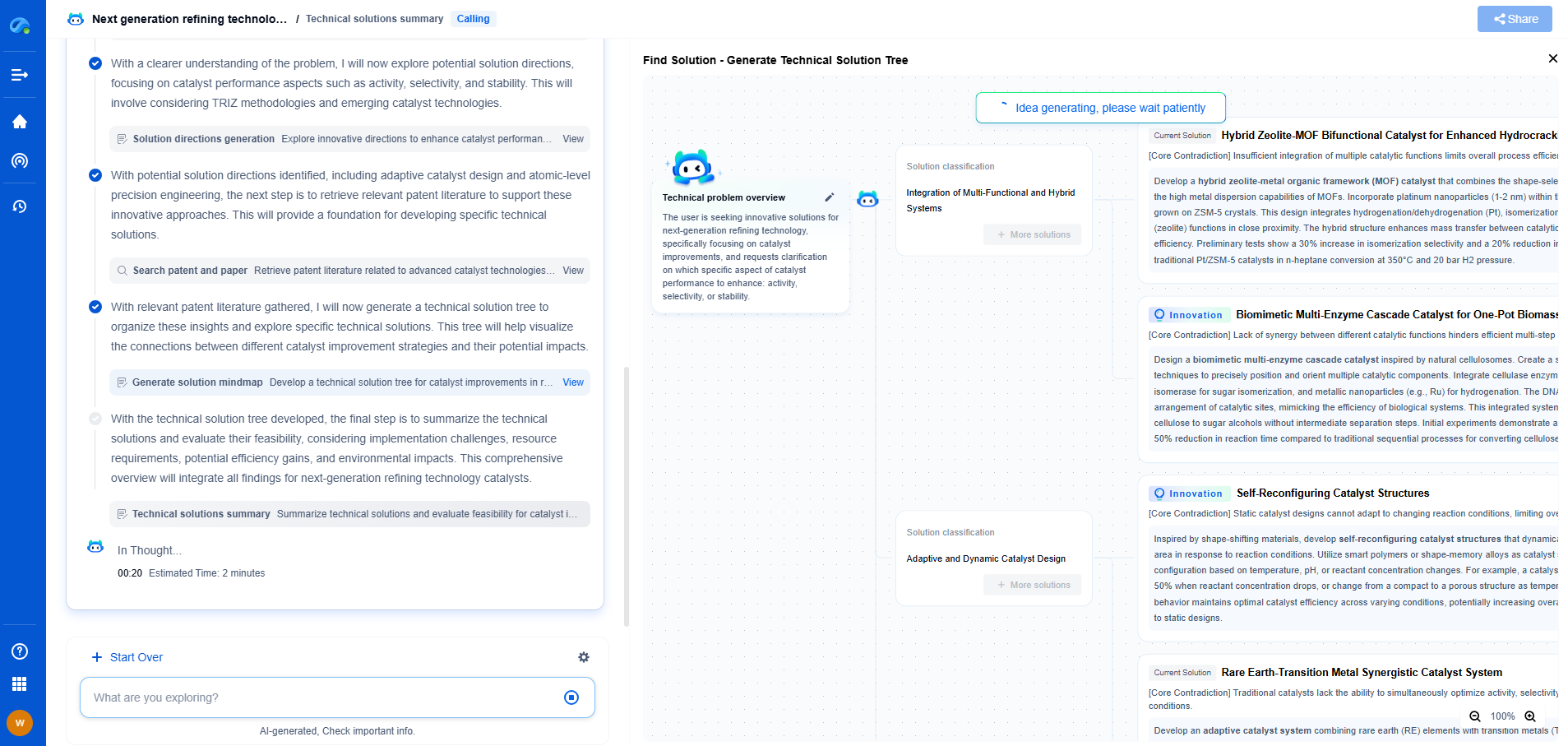
One can model the transient response using differential equations that describe the behavior over time. For linear time-invariant (LTI) systems, the Laplace transform is a powerful tool that simplifies the analysis by converting differential equations into algebraic equations. This transformation allows engineers to work in the complex frequency domain, making it easier to solve for transient and steady-state responses.

For example, consider an RC (resistor-capacitor) circuit subjected to a step voltage. The voltage across the capacitor as a function of time can be described by the equation V(t) = V0 * (1 - e^(-t/RC)), where V0 is the final steady-state voltage, R is the resistance, and C is the capacitance. The term RC is known as the time constant and determines how quickly the circuit responds to the change.

Types of Transient Responses

Transient responses can be categorized based on their characteristics:

1. Overdamped: The system returns to equilibrium without oscillating. This type occurs when the damping is strong, and the transient response is slow and monotonous.
2. Underdamped: The system oscillates with a gradually decreasing amplitude before settling. This is common in circuits with low damping.
3. Critically damped: The system returns to equilibrium as quickly as possible without oscillating. This is often the ideal response for many systems.
4. Oscillatory: The system exhibits sustained or decaying oscillations before reaching a steady state.

Practical Applications

Understanding transient response is crucial in various applications. In signal processing, it impacts how filters respond to changes, potentially affecting the signal integrity. In power electronics, transient analysis helps in designing circuits that can handle sudden changes in load without malfunctioning. Additionally, in communication systems, the transient behavior of circuits influences signal propagation and quality.

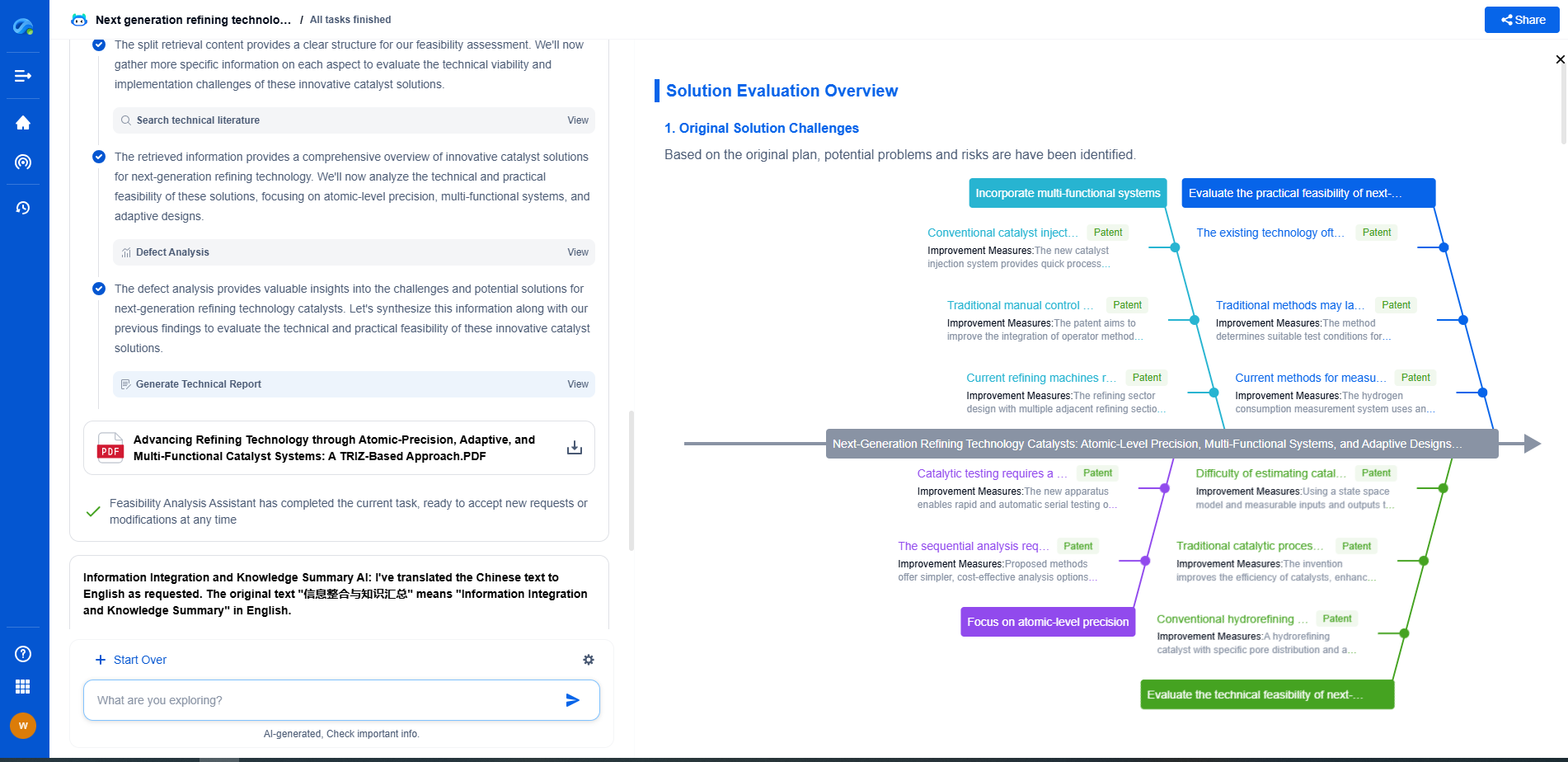
Challenges and Considerations

Several challenges arise when investigating transient response. Nonlinear components, parasitic elements, and external disturbances can complicate the analysis. Engineers must also consider the effect of temperature, component tolerances, and manufacturing variances on transient behavior.

In practical design, ensuring that the transient response meets the desired specifications is critical. It often involves trade-offs between speed and stability. For instance, in a power supply circuit, a fast transient response is desired for quick load changes, but it must be stable to prevent oscillations or overshoots.

Conclusion

The transient response of electronic circuits is an intricate subject that blends theoretical knowledge with practical application. By understanding how circuits react to changes, engineers can design more robust and efficient systems. While mathematical tools such as differential equations and Laplace transforms provide a framework for analysis, real-world applications require a deeper insight into material properties, component behavior, and system dynamics. As technology advances, the demand for circuits with precise transient responses continues to grow, underscoring the importance of mastering this crucial aspect of electronic design.