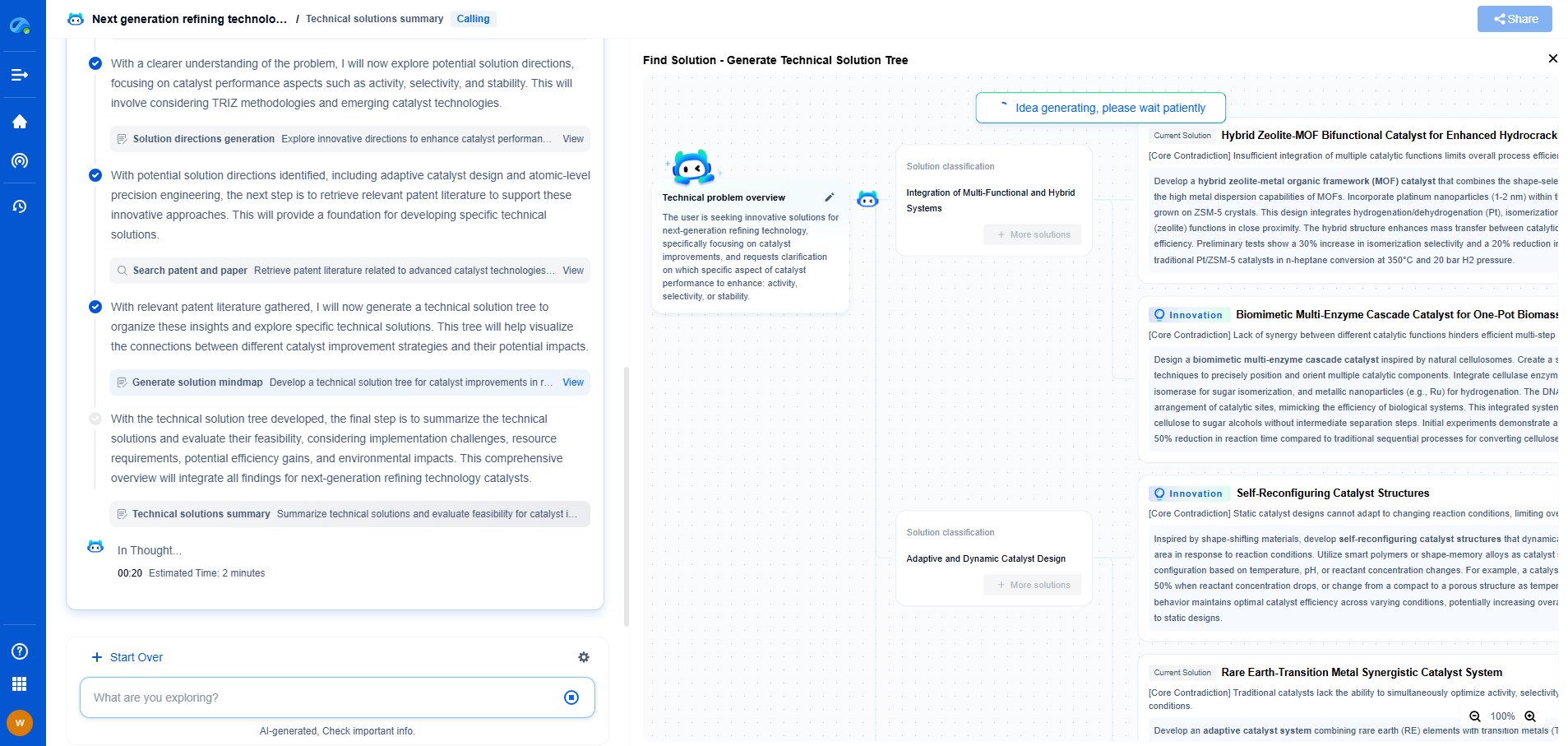
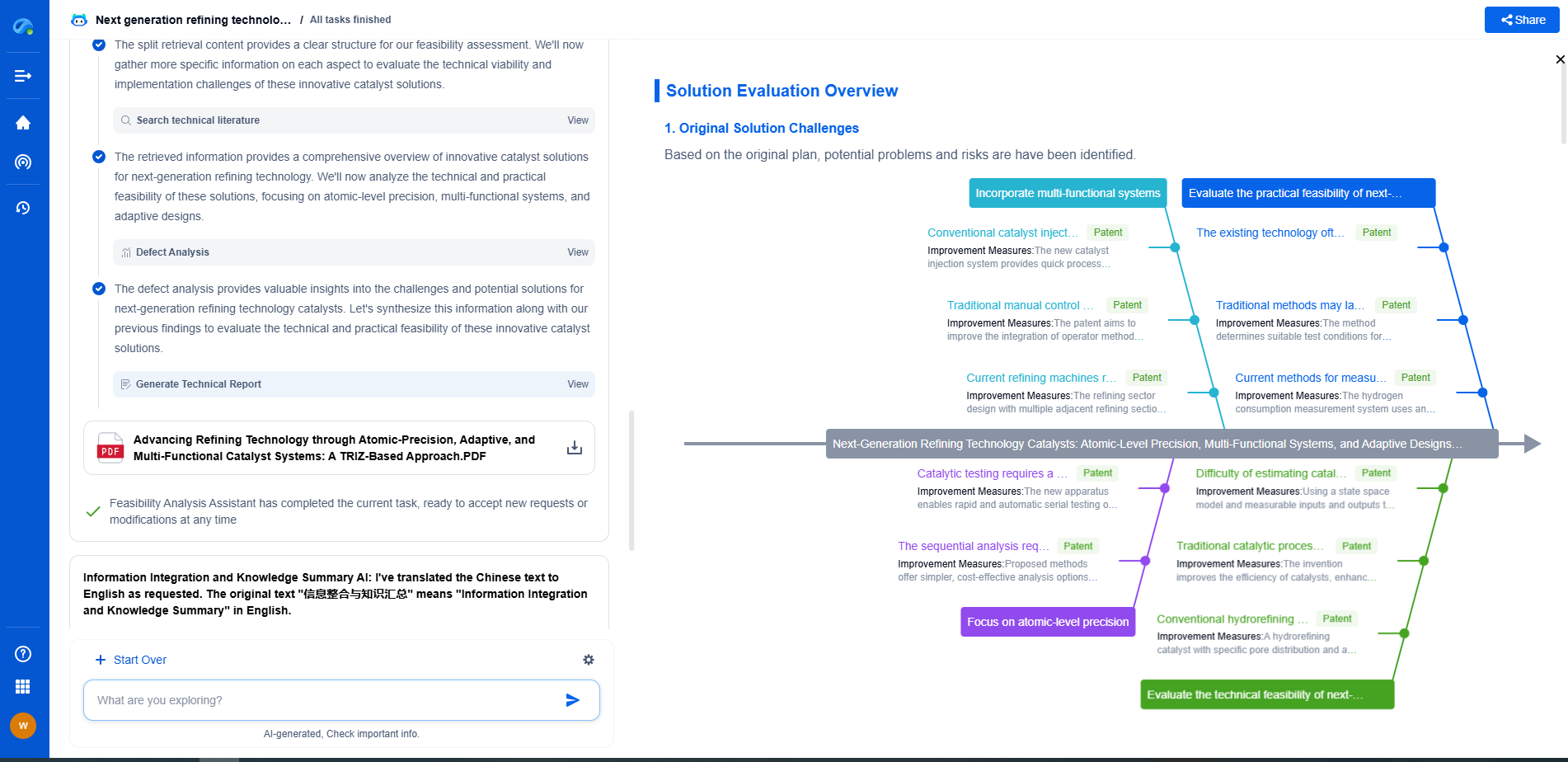
What is H∞ (H-infinity) Control? Robust Performance in Uncertain Systems
JUL 2, 2025 |
In the realm of control systems, handling uncertainty and ensuring robust performance is paramount. One approach that has gained significant attention is H∞ (H-infinity) control. This methodology is rooted in robust control theory and is particularly effective in dealing with systems where uncertainty is a major concern. H∞ control emphasizes designing controllers that can maintain performance within acceptable levels, even when faced with model inaccuracies or external disturbances.
Understanding Robust Control
Robust control is a field that focuses on maintaining system stability and performance despite uncertainties. These uncertainties can arise from various sources such as modeling errors, external disturbances, or parameter variations. Traditional control approaches often fall short when systems deviate from their nominal conditions. This is where robust control, including H∞ control, becomes critically important. It provides tools and methods to design controllers that are less sensitive to these uncertainties, ensuring that the system behaves reliably in real-world scenarios.
The Essence of H∞ Control
At its core, H∞ control is about minimizing the worst-case scenario. It seeks to design controllers that optimize performance under the worst possible disturbances and uncertainties. The term "H∞" comes from mathematical terms where "H" represents a space of transfer functions that describe the system dynamics, and "∞" signifies the infinity norm. This norm measures the maximum gain of the system response over all frequencies, which is a crucial consideration in achieving robustness.
Key Concepts and Mathematical Background
To delve deeper, it’s important to grasp some key concepts underlying H∞ control. The approach involves framing the control problem in a mathematical manner, specifically as an optimization problem. This involves minimizing the H∞ norm of the transfer function from the disturbance to the controlled output. By doing so, the method ensures that the system's response to disturbances is minimized across all possible frequencies.
Mathematically, the H∞ norm is defined as the supremum of the singular value of the system's transfer function over the imaginary axis. The challenge lies in finding a controller that achieves this minimization while ensuring system stability. Tools such as Riccati equations and linear matrix inequalities (LMIs) are often employed to solve this optimization problem.
Advantages of H∞ Control
One of the notable advantages of H∞ control is its robustness. By focusing on the worst-case scenario, H∞ controllers are inherently designed to handle a wide range of uncertainties. This makes them highly suitable for applications where system parameters are not well-known or can vary significantly.
Furthermore, H∞ control provides a systematic framework that can be applied to a variety of systems, from aerospace to automotive engineering. It offers a level of performance guarantee that is often difficult to achieve with traditional control methods.
Applications in Real-World Systems
H∞ control has found applications across numerous industries. In aerospace engineering, for instance, it is used to design flight control systems that remain stable and efficient despite external disturbances such as turbulence or changes in aircraft dynamics. In the automotive sector, H∞ controllers are employed to design advanced suspension systems that can adapt to varying road conditions.
The methodology is also applicable in the field of robotics, where systems must operate reliably in dynamic and uncertain environments. Additionally, H∞ control is leveraged in power systems to ensure the stability and reliability of electrical grids, even in the presence of load fluctuations and component failures.
Challenges and Considerations
While H∞ control offers robust solutions, it is not without its challenges. The design process can be mathematically complex and computationally intensive, particularly for high-dimensional systems. Moreover, achieving the desired robustness may require trade-offs with other performance metrics, such as transient response or energy efficiency.
It is crucial for engineers to carefully consider these trade-offs and understand the specific requirements of their application. Additionally, the implementation of H∞ controllers necessitates a thorough understanding of the system dynamics and the nature of the uncertainties involved.
Conclusion
H∞ control stands as a powerful tool in the robust control arsenal, offering a structured approach to managing uncertainties in complex systems. By prioritizing the worst-case scenario, it ensures that systems remain stable and perform effectively in real-world conditions. As industries continue to evolve and systems become increasingly complex, the importance of robust control methodologies like H∞ control will only grow, paving the way for more reliable and efficient technological advancements.
Ready to Reinvent How You Work on Control Systems?
Designing, analyzing, and optimizing control systems involves complex decision-making, from selecting the right sensor configurations to ensuring robust fault tolerance and interoperability. If you’re spending countless hours digging through documentation, standards, patents, or simulation results — it's time for a smarter way to work.
Patsnap Eureka is your intelligent AI Agent, purpose-built for R&D and IP professionals in high-tech industries. Whether you're developing next-gen motion controllers, debugging signal integrity issues, or navigating complex regulatory and patent landscapes in industrial automation, Eureka helps you cut through technical noise and surface the insights that matter—faster.
👉 Experience Patsnap Eureka today — Power up your Control Systems innovation with AI intelligence built for engineers and IP minds.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com