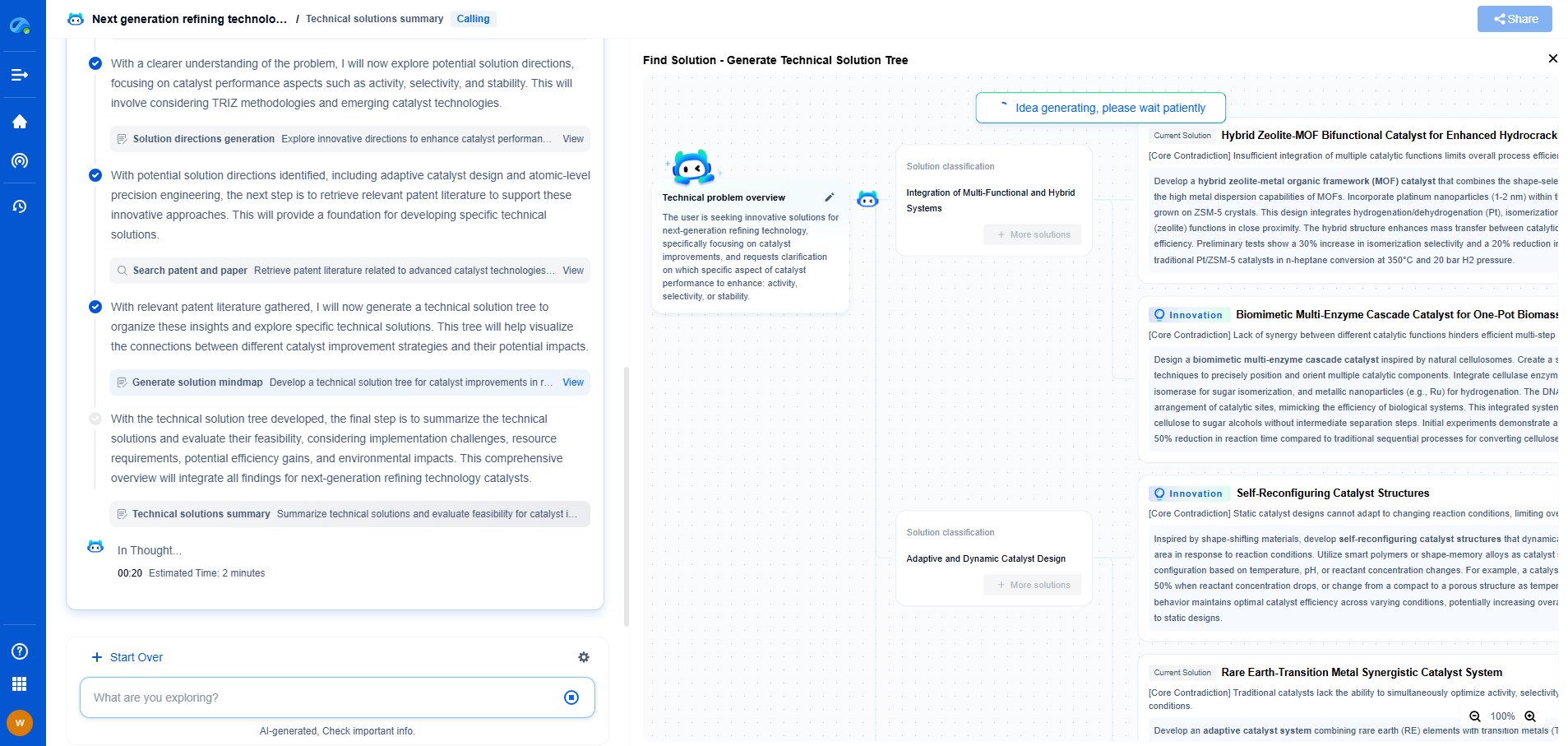
What is PID Control and How Does It Work?
JUL 2, 2025 |
PID control, which stands for Proportional-Integral-Derivative control, is a widely used control loop feedback mechanism in industrial control systems. It is employed to regulate temperature, speed, flow, pressure, and many other process variables in a diverse range of industries. Understanding the PID controller is crucial for anyone involved in process control or automation, as it is fundamental to maintaining desired outputs in various applications.
Components of a PID Controller
A PID controller consists of three main components: Proportional, Integral, and Derivative. Each plays a unique role in achieving control over a process variable.
1. Proportional Control
The proportional component of a PID controller provides an output that is proportional to the current error value. The error is the difference between the desired setpoint and the current process variable. The proportional gain, denoted as Kp, adjusts the response to the error. A higher Kp results in a stronger reaction to the error, which can lead to faster correction but may also cause overshooting the setpoint if not carefully tuned.
2. Integral Control
The integral component focuses on eliminating the residual steady-state error that can occur with proportional control alone. It integrates the error over time, providing a correction based on the accumulated error. The integral gain, Ki, determines the speed at which the integral action builds. However, too high of an integral gain can lead to oscillations or instability within the system.
3. Derivative Control
The derivative component predicts the future trend of the error based on its current rate of change. By responding to the rate at which the error is changing, the derivative action can anticipate future errors and apply corrective actions accordingly. The derivative gain, Kd, adjusts the sensitivity to the rate of change of the error. While beneficial in dampening oscillations, excessive derivative gain can amplify noise and lead to erratic control behavior.
How PID Control Works
Integration of the three components allows a PID controller to offer a balanced control response. Each part compensates for the weaknesses of the others, creating a robust system that can handle a wide array of control challenges. The PID controller continuously calculates an error value and applies a correction based on proportional, integral, and derivative terms, which are summed to produce the control variable.
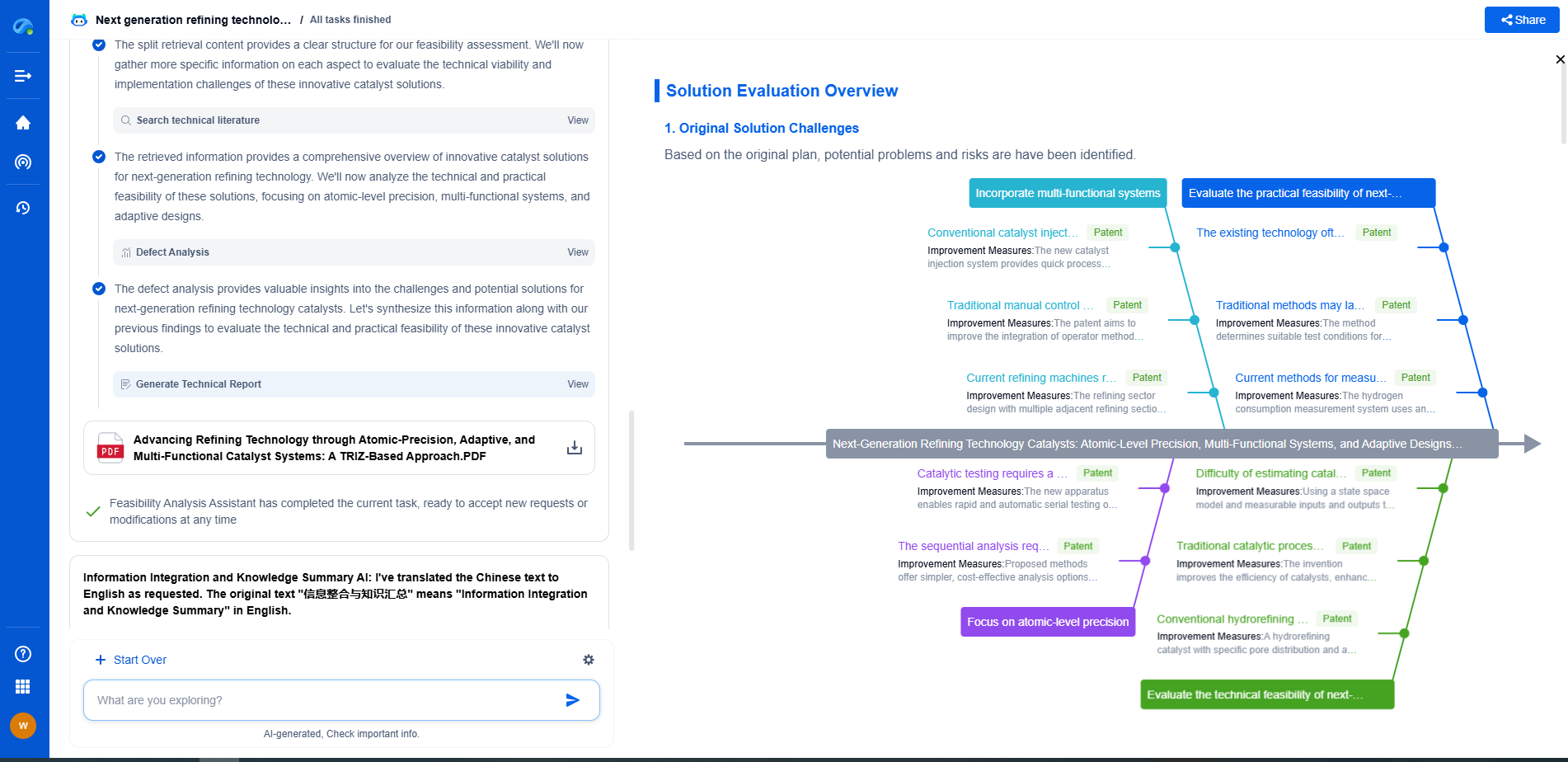
Tuning a PID Controller
Tuning a PID controller is an essential step to ensure it performs optimally in a given process. The process involves setting the proportional, integral, and derivative gains to achieve the desired response. Several methods exist for tuning, including:
1. Manual Tuning
Manual tuning involves adjusting the gains based on observation and experience. This method can be time-consuming and requires a deep understanding of the process dynamics.
2. Ziegler-Nichols Method
A widely used empirical method, the Ziegler-Nichols method provides set rules for setting the PID parameters based on the system's response to certain test inputs. It is particularly useful in systems where manual tuning is not feasible.
3. Software Tools
Various software tools and systems offer automated PID tuning, leveraging algorithms to find optimal parameters quickly. These tools can be advantageous in complex systems where human intuition may fall short.
Applications of PID Control
PID controllers are found in countless applications across industries. In manufacturing, they are used to regulate processes like temperature control in furnaces or speed control in motors. In the automotive industry, PID control is applied in cruise control systems to maintain a constant vehicle speed. Moreover, in the aerospace sector, PID controllers are crucial for maintaining the stability and control of aircraft.
Advantages and Limitations
The key advantage of PID control is its simplicity and effectiveness in a wide range of applications. It is relatively easy to implement and provides robust control without requiring a detailed model of the system. However, PID controllers have limitations, particularly in systems with significant time delays or where system dynamics are highly nonlinear. In such cases, advanced control strategies may be required.
Conclusion
PID control remains a cornerstone of process control and automation, offering a straightforward yet powerful solution for maintaining desired outputs across various systems. Understanding its components and how they interact provides valuable insights into optimizing system performance. While it has limitations, the adaptability and reliability of PID control ensure its continued relevance in modern industrial applications.
Ready to Reinvent How You Work on Control Systems?
Designing, analyzing, and optimizing control systems involves complex decision-making, from selecting the right sensor configurations to ensuring robust fault tolerance and interoperability. If you’re spending countless hours digging through documentation, standards, patents, or simulation results — it's time for a smarter way to work.
Patsnap Eureka is your intelligent AI Agent, purpose-built for R&D and IP professionals in high-tech industries. Whether you're developing next-gen motion controllers, debugging signal integrity issues, or navigating complex regulatory and patent landscapes in industrial automation, Eureka helps you cut through technical noise and surface the insights that matter—faster.
👉 Experience Patsnap Eureka today — Power up your Control Systems innovation with AI intelligence built for engineers and IP minds.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com