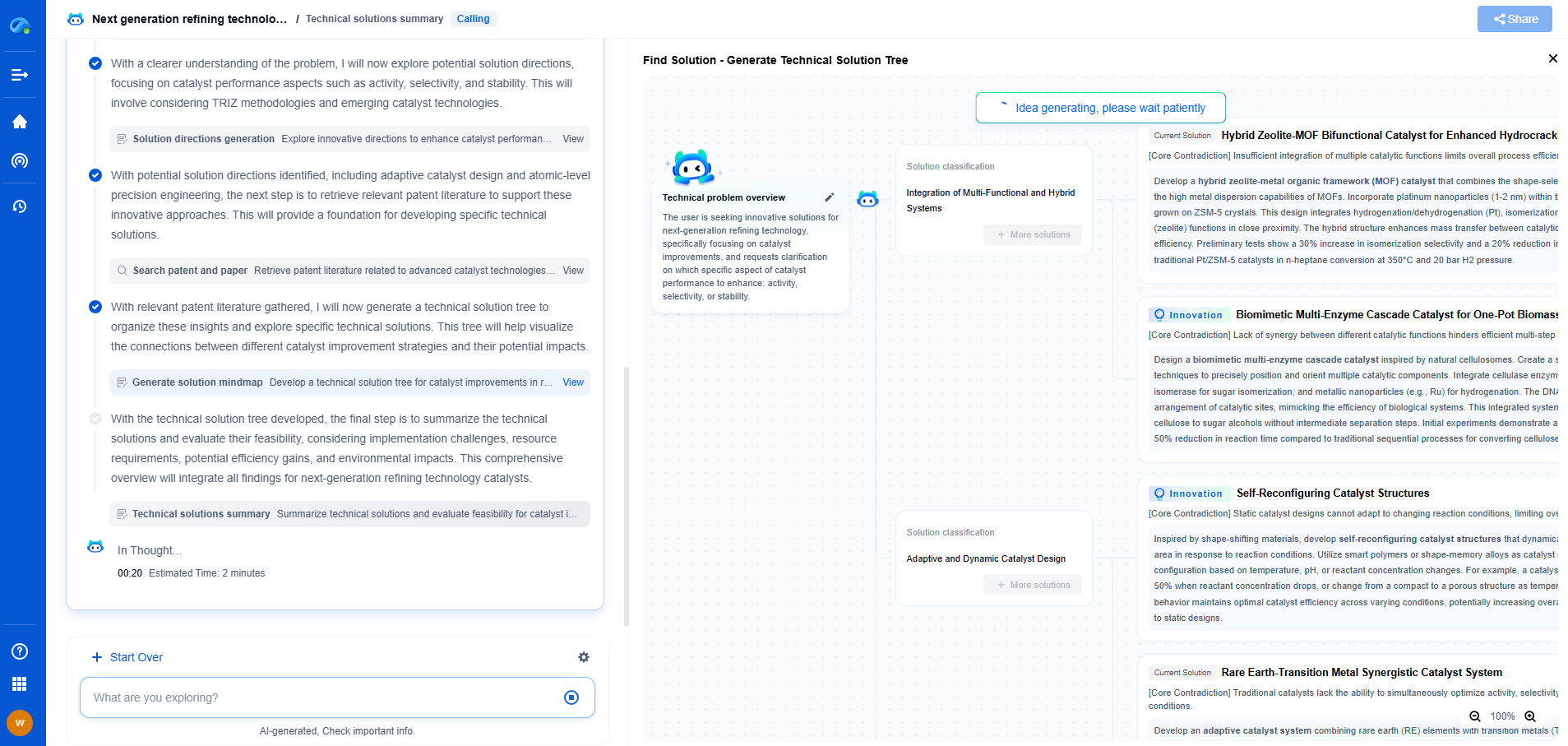
What is Signal Convolution and How is it Used in Filtering?
JUN 27, 2025 |
Signal convolution is a fundamental concept in signal processing that plays a crucial role in various applications, particularly in filtering. Convolution is a mathematical operation that blends two signals to produce a third signal that represents how the shape of one is modified by the other. This process helps in analyzing how different systems affect signals, which is essential in numerous fields such as audio and image processing, telecommunications, and control systems. Understanding signal convolution can provide valuable insights into the behavior of signals as they pass through different systems.
The Mathematics Behind Convolution
Mathematically, convolution is represented by the integral of the product of two functions after one is reversed and shifted. For continuous signals, the convolution of two functions, f(t) and g(t), is defined as:
(f * g)(t) = ∫ f(τ) g(t - τ) dτ
where τ is a dummy variable of integration. For discrete signals, the convolution sum is used:
(f * g)[n] = Σ f[k] g[n - k]
where n and k are indices of the discrete signals.
The operation can be visualized as sliding one signal over another and computing the integral (or sum) of their product at each point. This process highlights the effect of one signal on another, which is particularly useful in signal filtering.
Convolution in Filtering
Filtering is a process used to extract specific parts of a signal while minimizing others, often to remove noise or enhance particular features. Convolution is central to filtering operations, especially linear time-invariant (LTI) systems.
In filtering, the input signal is convolved with a filter kernel or impulse response. The filter kernel determines the characteristics of the filter, such as its frequency response. Depending on the application, filters can be designed to be low-pass, high-pass, band-pass, or band-stop, each serving to allow or attenuate specific frequency ranges.
Low-pass filters, for instance, allow signals with a frequency lower than a certain cutoff frequency to pass through while attenuating higher frequencies. This is particularly useful in reducing noise or smoothing signals. High-pass filters do the opposite, attenuating low frequencies and allowing higher frequencies to pass, which can help in edge detection in image processing.
Applications of Convolution in Signal Processing
Convolution has a wide range of applications across different domains:
1. Audio Processing: In audio, convolution is used to apply effects such as reverb and echo by convolving an audio signal with an impulse response recorded in a specific environment. This technique allows sound engineers to replicate the acoustics of famous concert halls and studios.
2. Image Processing: Convolution is extensively used in image processing tasks like blurring, sharpening, and edge detection. Convolutional neural networks (CNNs), which are inspired by the convolution operation, have revolutionized computer vision by enabling machines to recognize and classify images with high accuracy.
3. Telecommunications: In communication systems, convolution is used in the design of equalizers that mitigate the effects of signal distortion during transmission. This ensures better quality and reliability of data transmission over various channels.
4. Control Systems: Convolution is used in control systems to analyze how input signals affect the output of dynamic systems. This is crucial for designing systems with stable and desired responses.
Conclusion
Signal convolution is a powerful tool that underlies many signal processing techniques, particularly in filtering applications. By understanding and leveraging convolution, engineers and scientists can design systems that effectively manipulate signals to achieve desired outcomes. Whether in audio and image processing or telecommunications and control systems, convolution remains an indispensable operation that enhances our ability to interact with and interpret signals.
Accelerate Electronic Circuit Innovation with AI-Powered Insights from Patsnap Eureka
The world of electronic circuits is evolving faster than ever—from high-speed analog signal processing to digital modulation systems, PLLs, oscillators, and cutting-edge power management ICs. For R&D engineers, IP professionals, and strategic decision-makers in this space, staying ahead of the curve means navigating a massive and rapidly growing landscape of patents, technical literature, and competitor moves.
Patsnap Eureka, our intelligent AI assistant built for R&D professionals in high-tech sectors, empowers you with real-time expert-level analysis, technology roadmap exploration, and strategic mapping of core patents—all within a seamless, user-friendly interface.
🚀 Experience the next level of innovation intelligence. Try Patsnap Eureka today and discover how AI can power your breakthroughs in electronic circuit design and strategy. Book a free trial or schedule a personalized demo now.
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com