Understanding Optimization in Machine Learning

In the world of machine learning, the process of optimization plays a crucial role. Optimization algorithms are used to adjust the weights of neural networks to minimize the error or cost function. Two popular optimization algorithms often discussed are Stochastic Gradient Descent (SGD) and the Adam optimizer. Both have their advantages and disadvantages, but many practitioners have found Adam to outperform SGD in various scenarios. This article delves into the reasons why Adam optimizer often yields better results and explores the concept of adaptive momentum behind its success.

The Basics of SGD

To understand why Adam often outperforms SGD, it’s important to first grasp how SGD functions. Stochastic Gradient Descent is a version of gradient descent that uses only a single or a few training examples to compute the gradient and update the model parameters. This makes it much faster compared to traditional gradient descent, which uses the entire dataset. While SGD introduces noise into the optimization process by using fewer samples, it helps the algorithm escape local minima. However, SGD can converge to suboptimal points and may be slow to reach the global minimum, especially if the learning rate is not well-tuned.

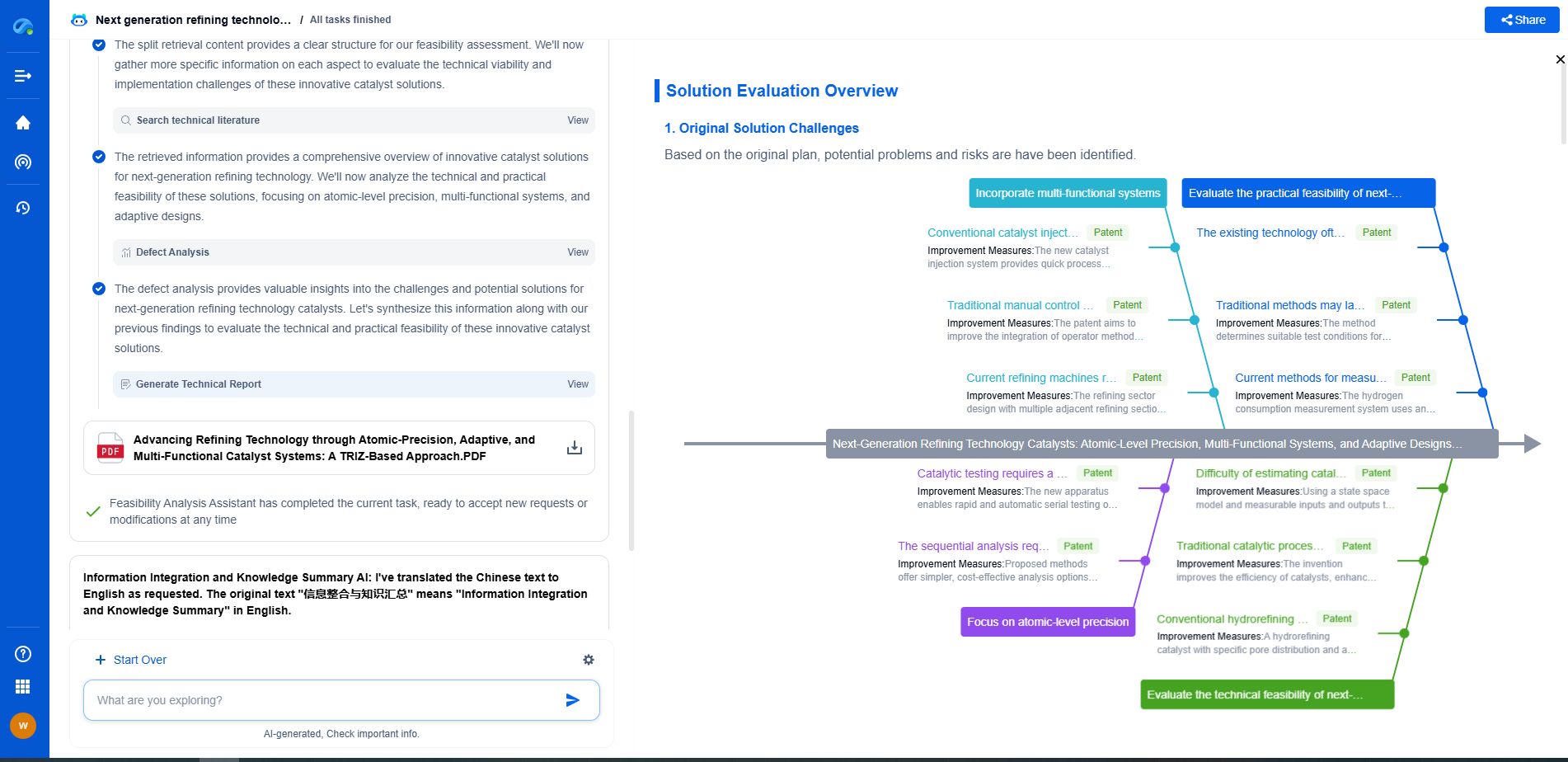
Limitations of SGD

Despite its widespread use, SGD suffers from several limitations. One of the primary challenges is selecting the appropriate learning rate. A learning rate that's too high can cause the algorithm to overshoot the minimum, while one that's too low can make the convergence painfully slow. Moreover, SGD does not adapt the learning rate during training, which can lead to inefficient updates, especially in areas of the cost function with different curvature. Additionally, SGD has trouble navigating ravines, which are areas where the surface curves much more steeply in one dimension than in another.

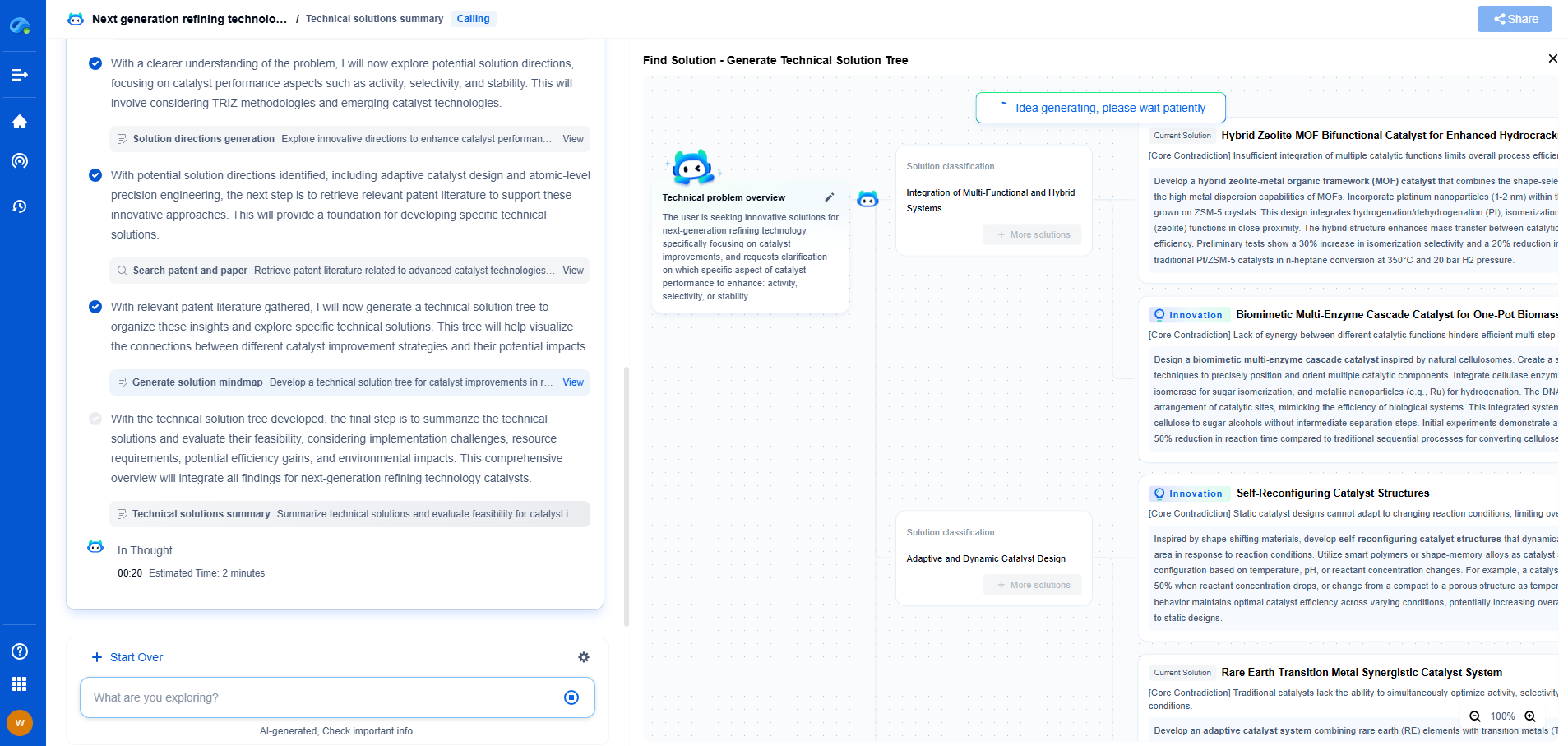
Introducing the Adam Optimizer

The Adam optimizer, short for Adaptive Moment Estimation, is designed to overcome some of the limitations inherent in SGD. Developed by Diederik Kingma and Jimmy Ba in 2014, Adam combines the advantages of two other extensions of gradient descent: Adaptive Gradient Algorithm (AdaGrad) and Root Mean Square Propagation (RMSProp). By doing so, Adam is capable of adapting the learning rate for each parameter, effectively handling the diverse challenges posed by complex datasets.

Adaptive Learning Rates

One of the most significant advantages of the Adam optimizer is its ability to adapt the learning rate for each parameter dynamically. This is achieved by maintaining a per-parameter learning rate that adjusts over time based on the average of recent gradients (first moment) and the squares of recent gradients (second moment). This ensures that the learning process is more efficient and less sensitive to the initial learning rate setting, allowing Adam to converge faster than SGD in many cases.

Momentum and Its Role

Adam incorporates an advanced form of momentum. Momentum is a technique that helps accelerate SGD in the relevant direction and dampens oscillations. It does this by adding a fraction of the previous update to the current update. The Adam optimizer takes this a step further by using an exponentially decaying average of past gradients to smooth out the noise and stabilize the updates, which helps in achieving faster convergence.

Bias Correction

Another feature that sets Adam apart is its bias correction mechanism. In the early stages of training, the moving averages used to calculate the first and second moments are biased towards zero, especially when the decay rates are small. Adam corrects these biases to provide more accurate estimates, ensuring that the learning rate adjustments are more reliable and effective throughout the training process.

Practical Advantages

In practice, Adam is often preferred over SGD for several reasons. Its adaptive learning rates make it well-suited for problems with large data and parameters. The bias-corrected estimates of momentums facilitate more stable and faster convergence. Additionally, Adam’s performance is generally robust across a wide range of hyperparameters, making it a go-to choice for many machine learning practitioners who may not have the resources to perform extensive hyperparameter tuning.

Conclusion

While each optimization algorithm has its place and function, the Adam optimizer stands out for its adaptive learning rate and momentum parameters. These features allow it to handle the intricacies of diverse data landscapes more efficiently than SGD. By understanding the mechanics behind these algorithms, machine learning practitioners can make informed choices about which optimizer to use, ultimately leading to better model performance and faster convergence.