Quantum Computing's Impact on Statistical Mechanics
JUL 17, 202510 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Quantum Computing and Statistical Mechanics Overview
Quantum computing and statistical mechanics represent two fundamental pillars of modern physics, each with profound implications for our understanding of the natural world. The intersection of these fields has emerged as a frontier of scientific exploration, promising revolutionary advancements in both theoretical physics and practical applications.
Statistical mechanics, developed in the late 19th century, provides a framework for understanding the behavior of large systems of particles by applying statistical methods to the laws of classical mechanics. It has been instrumental in explaining phenomena such as phase transitions, thermodynamic properties, and the behavior of gases and liquids. However, the complexity of many-body systems often poses significant computational challenges, limiting our ability to model and predict certain phenomena accurately.
Quantum computing, on the other hand, harnesses the principles of quantum mechanics to perform computations that are infeasible for classical computers. By leveraging quantum superposition and entanglement, quantum computers have the potential to solve certain problems exponentially faster than their classical counterparts. This computational power holds particular promise for simulating quantum systems, a task that is notoriously difficult for classical computers due to the exponential growth of the Hilbert space with system size.
The convergence of quantum computing and statistical mechanics opens up new avenues for addressing long-standing challenges in condensed matter physics, materials science, and quantum chemistry. Quantum algorithms for simulating many-body systems could enable more accurate predictions of material properties, phase transitions, and chemical reactions. Moreover, quantum-inspired classical algorithms have already shown improvements in solving certain statistical mechanics problems, bridging the gap between quantum and classical approaches.
As quantum hardware continues to advance, researchers are exploring novel quantum algorithms tailored to statistical mechanics problems. These include variational quantum algorithms for finding ground states of complex Hamiltonians, quantum annealing for optimization problems, and quantum Monte Carlo methods for sampling from probability distributions. These approaches have the potential to revolutionize our ability to study and design materials, optimize complex systems, and unravel the mysteries of quantum many-body physics.
The impact of quantum computing on statistical mechanics extends beyond simulation and modeling. It also offers new perspectives on fundamental concepts such as entropy, thermalization, and quantum thermodynamics. Quantum information theory provides a fresh lens through which to view statistical mechanics, leading to insights into the nature of information, complexity, and the arrow of time.
As this field evolves, it promises not only to enhance our understanding of complex physical systems but also to drive innovations in quantum technologies, materials science, and beyond. The synergy between quantum computing and statistical mechanics represents a fertile ground for interdisciplinary research, with far-reaching implications for both theoretical physics and practical applications in the coming decades.
Statistical mechanics, developed in the late 19th century, provides a framework for understanding the behavior of large systems of particles by applying statistical methods to the laws of classical mechanics. It has been instrumental in explaining phenomena such as phase transitions, thermodynamic properties, and the behavior of gases and liquids. However, the complexity of many-body systems often poses significant computational challenges, limiting our ability to model and predict certain phenomena accurately.
Quantum computing, on the other hand, harnesses the principles of quantum mechanics to perform computations that are infeasible for classical computers. By leveraging quantum superposition and entanglement, quantum computers have the potential to solve certain problems exponentially faster than their classical counterparts. This computational power holds particular promise for simulating quantum systems, a task that is notoriously difficult for classical computers due to the exponential growth of the Hilbert space with system size.
The convergence of quantum computing and statistical mechanics opens up new avenues for addressing long-standing challenges in condensed matter physics, materials science, and quantum chemistry. Quantum algorithms for simulating many-body systems could enable more accurate predictions of material properties, phase transitions, and chemical reactions. Moreover, quantum-inspired classical algorithms have already shown improvements in solving certain statistical mechanics problems, bridging the gap between quantum and classical approaches.
As quantum hardware continues to advance, researchers are exploring novel quantum algorithms tailored to statistical mechanics problems. These include variational quantum algorithms for finding ground states of complex Hamiltonians, quantum annealing for optimization problems, and quantum Monte Carlo methods for sampling from probability distributions. These approaches have the potential to revolutionize our ability to study and design materials, optimize complex systems, and unravel the mysteries of quantum many-body physics.
The impact of quantum computing on statistical mechanics extends beyond simulation and modeling. It also offers new perspectives on fundamental concepts such as entropy, thermalization, and quantum thermodynamics. Quantum information theory provides a fresh lens through which to view statistical mechanics, leading to insights into the nature of information, complexity, and the arrow of time.
As this field evolves, it promises not only to enhance our understanding of complex physical systems but also to drive innovations in quantum technologies, materials science, and beyond. The synergy between quantum computing and statistical mechanics represents a fertile ground for interdisciplinary research, with far-reaching implications for both theoretical physics and practical applications in the coming decades.
Market Demand for Quantum-Enhanced Statistical Analysis
The market demand for quantum-enhanced statistical analysis is rapidly growing as industries recognize the potential of quantum computing to revolutionize complex problem-solving in statistical mechanics. This emerging field offers unprecedented computational power to tackle challenges that were previously intractable using classical methods.
In the financial sector, quantum-enhanced statistical analysis is gaining traction for risk assessment and portfolio optimization. Banks and investment firms are exploring quantum algorithms to model market dynamics more accurately, potentially leading to better investment strategies and risk management. The ability to process vast amounts of financial data and consider multiple variables simultaneously makes quantum computing particularly attractive for this industry.
The pharmaceutical and biotechnology sectors are also showing keen interest in quantum-enhanced statistical analysis. Drug discovery processes, which often involve complex molecular simulations, stand to benefit significantly from quantum computing's ability to model quantum mechanical systems more efficiently. This could potentially accelerate the development of new drugs and reduce associated costs.
Climate modeling and weather prediction represent another area with substantial market demand for quantum-enhanced statistical analysis. The complexity of Earth's climate system requires immense computational resources, and quantum computing could provide more accurate long-term forecasts and improve our understanding of climate change dynamics.
In the energy sector, optimization of power grids and energy distribution networks is a promising application for quantum-enhanced statistical analysis. The ability to handle large-scale optimization problems more efficiently could lead to significant improvements in energy efficiency and cost reduction.
The manufacturing industry is exploring quantum computing for supply chain optimization and quality control processes. By analyzing vast amounts of data from sensors and production lines, quantum-enhanced statistical analysis could help identify inefficiencies and predict maintenance needs more accurately.
As quantum hardware continues to advance, the market for quantum-enhanced statistical analysis software and services is expected to grow substantially. This includes the development of quantum algorithms, quantum-classical hybrid solutions, and quantum-ready applications that can leverage the power of quantum systems as they become more widely available.
However, it's important to note that the market is still in its early stages, with many potential applications still in the research and development phase. The full realization of quantum-enhanced statistical analysis's market potential will depend on continued advancements in quantum hardware, the development of practical quantum algorithms, and the ability to integrate quantum solutions with existing classical infrastructure.
In the financial sector, quantum-enhanced statistical analysis is gaining traction for risk assessment and portfolio optimization. Banks and investment firms are exploring quantum algorithms to model market dynamics more accurately, potentially leading to better investment strategies and risk management. The ability to process vast amounts of financial data and consider multiple variables simultaneously makes quantum computing particularly attractive for this industry.
The pharmaceutical and biotechnology sectors are also showing keen interest in quantum-enhanced statistical analysis. Drug discovery processes, which often involve complex molecular simulations, stand to benefit significantly from quantum computing's ability to model quantum mechanical systems more efficiently. This could potentially accelerate the development of new drugs and reduce associated costs.
Climate modeling and weather prediction represent another area with substantial market demand for quantum-enhanced statistical analysis. The complexity of Earth's climate system requires immense computational resources, and quantum computing could provide more accurate long-term forecasts and improve our understanding of climate change dynamics.
In the energy sector, optimization of power grids and energy distribution networks is a promising application for quantum-enhanced statistical analysis. The ability to handle large-scale optimization problems more efficiently could lead to significant improvements in energy efficiency and cost reduction.
The manufacturing industry is exploring quantum computing for supply chain optimization and quality control processes. By analyzing vast amounts of data from sensors and production lines, quantum-enhanced statistical analysis could help identify inefficiencies and predict maintenance needs more accurately.
As quantum hardware continues to advance, the market for quantum-enhanced statistical analysis software and services is expected to grow substantially. This includes the development of quantum algorithms, quantum-classical hybrid solutions, and quantum-ready applications that can leverage the power of quantum systems as they become more widely available.
However, it's important to note that the market is still in its early stages, with many potential applications still in the research and development phase. The full realization of quantum-enhanced statistical analysis's market potential will depend on continued advancements in quantum hardware, the development of practical quantum algorithms, and the ability to integrate quantum solutions with existing classical infrastructure.
Current Challenges in Quantum Statistical Mechanics
The field of quantum statistical mechanics currently faces several significant challenges that hinder its progress and application. One of the primary obstacles is the complexity of quantum systems, which grows exponentially with the number of particles involved. This makes it computationally intractable to simulate large-scale quantum systems using classical computers, limiting our ability to study and predict the behavior of complex quantum materials and phenomena.
Another major challenge lies in the development of efficient algorithms for quantum simulation. While quantum computers hold promise for simulating quantum systems more efficiently than classical computers, designing and implementing effective quantum algorithms for statistical mechanics problems remains a formidable task. Researchers are still working on optimizing quantum algorithms to handle the intricacies of many-body quantum systems and their statistical properties.
The measurement problem in quantum mechanics also poses a significant challenge for quantum statistical mechanics. The act of measurement in quantum systems can fundamentally alter the state of the system, making it difficult to obtain accurate statistical information without disturbing the system's quantum properties. This inherent uncertainty complicates the process of gathering reliable statistical data from quantum systems.
Furthermore, the interplay between quantum effects and thermal fluctuations presents a complex landscape for researchers. Understanding how quantum coherence and entanglement persist or decay in the presence of thermal noise is crucial for developing accurate models of quantum statistical systems. This challenge becomes particularly acute when studying quantum phase transitions and critical phenomena in many-body systems.
The lack of experimental techniques to probe quantum statistical properties at the microscopic level also hampers progress in the field. While advances in quantum sensing and metrology have improved our ability to measure quantum systems, there is still a significant gap between theoretical predictions and experimental verifications in many areas of quantum statistical mechanics.
Lastly, the integration of quantum statistical mechanics with other fields, such as quantum information theory and condensed matter physics, presents both opportunities and challenges. Bridging these disciplines requires a multidisciplinary approach and the development of new theoretical frameworks that can effectively describe the statistical behavior of quantum systems across different scales and in various contexts.
Another major challenge lies in the development of efficient algorithms for quantum simulation. While quantum computers hold promise for simulating quantum systems more efficiently than classical computers, designing and implementing effective quantum algorithms for statistical mechanics problems remains a formidable task. Researchers are still working on optimizing quantum algorithms to handle the intricacies of many-body quantum systems and their statistical properties.
The measurement problem in quantum mechanics also poses a significant challenge for quantum statistical mechanics. The act of measurement in quantum systems can fundamentally alter the state of the system, making it difficult to obtain accurate statistical information without disturbing the system's quantum properties. This inherent uncertainty complicates the process of gathering reliable statistical data from quantum systems.
Furthermore, the interplay between quantum effects and thermal fluctuations presents a complex landscape for researchers. Understanding how quantum coherence and entanglement persist or decay in the presence of thermal noise is crucial for developing accurate models of quantum statistical systems. This challenge becomes particularly acute when studying quantum phase transitions and critical phenomena in many-body systems.
The lack of experimental techniques to probe quantum statistical properties at the microscopic level also hampers progress in the field. While advances in quantum sensing and metrology have improved our ability to measure quantum systems, there is still a significant gap between theoretical predictions and experimental verifications in many areas of quantum statistical mechanics.
Lastly, the integration of quantum statistical mechanics with other fields, such as quantum information theory and condensed matter physics, presents both opportunities and challenges. Bridging these disciplines requires a multidisciplinary approach and the development of new theoretical frameworks that can effectively describe the statistical behavior of quantum systems across different scales and in various contexts.
Existing Quantum Algorithms for Statistical Mechanics
01 Quantum Circuit Design and Optimization
This area focuses on developing and optimizing quantum circuits for various applications. It involves creating efficient quantum gate sequences, reducing circuit depth, and improving qubit connectivity. Techniques may include circuit compression, gate decomposition, and topology-aware mapping to enhance the performance of quantum algorithms on real quantum hardware.- Quantum computing architectures: Various quantum computing architectures are being developed to improve qubit stability, scalability, and error correction. These include superconducting circuits, trapped ions, topological qubits, and photonic systems. Each architecture has its own advantages and challenges in terms of coherence time, gate fidelity, and integration with classical computing systems.
- Quantum error correction and fault tolerance: Quantum error correction techniques are crucial for maintaining the integrity of quantum information in the presence of noise and decoherence. Fault-tolerant quantum computing schemes are being developed to enable large-scale quantum computations. These include surface codes, color codes, and other topological quantum codes that can protect quantum information from errors.
- Quantum algorithms and applications: Quantum algorithms are being developed to solve complex problems more efficiently than classical computers. These include algorithms for optimization, machine learning, cryptography, and simulation of quantum systems. Potential applications span fields such as finance, drug discovery, materials science, and artificial intelligence.
- Quantum-classical hybrid systems: Hybrid quantum-classical systems combine the strengths of quantum and classical computing. These systems use quantum processors for specific tasks while leveraging classical computers for control, data processing, and interfacing. This approach allows for near-term practical applications of quantum computing and facilitates the integration of quantum technologies into existing computing infrastructures.
- Quantum communication and networking: Quantum communication technologies enable secure data transmission using quantum key distribution and other quantum cryptographic protocols. Quantum networks are being developed to connect multiple quantum processors, allowing for distributed quantum computing and the creation of a quantum internet. These advancements have implications for secure communications, distributed sensing, and large-scale quantum information processing.
02 Error Correction and Fault Tolerance
Error correction and fault tolerance are crucial for building reliable quantum computers. This field involves developing techniques to detect and correct quantum errors, implementing fault-tolerant quantum gates, and designing quantum error correction codes. These methods aim to mitigate the effects of decoherence and improve the overall stability of quantum systems.Expand Specific Solutions03 Quantum-Classical Hybrid Algorithms
Hybrid algorithms combine classical and quantum computing to leverage the strengths of both paradigms. This approach involves developing algorithms that use quantum processors for specific subroutines while relying on classical computers for other parts of the computation. Such hybrid methods are particularly useful for near-term quantum devices with limited qubit counts and coherence times.Expand Specific Solutions04 Quantum Machine Learning
Quantum machine learning explores the intersection of quantum computing and machine learning. This field involves developing quantum algorithms for tasks such as classification, clustering, and optimization. Researchers are investigating how quantum computers can potentially speed up certain machine learning tasks or handle complex data structures more efficiently than classical computers.Expand Specific Solutions05 Quantum Hardware Architecture
This area focuses on the physical implementation of quantum computers, including the design of qubits, quantum gates, and control systems. It involves research into various qubit technologies such as superconducting circuits, trapped ions, and topological qubits. The goal is to develop scalable and robust quantum hardware architectures that can support large-scale quantum computations.Expand Specific Solutions
Key Players in Quantum Computing and Statistical Mechanics
The quantum computing landscape in statistical mechanics is evolving rapidly, with the field currently in a transitional phase from theoretical research to practical applications. The market size is expanding, driven by increasing investments from both public and private sectors. While the technology is still maturing, significant progress has been made in recent years. Key players like IBM, Google, and Intel are leading the charge in hardware development, while specialized quantum companies such as Terra Quantum AG and Origin Quantum are focusing on software and applications. Universities like Sussex, Chicago, and Delft are contributing crucial research. The competition is intensifying as more companies enter the field, with a mix of established tech giants and innovative startups vying for dominance in this potentially transformative technology.
Intel Corp.
Technical Solution: Intel's contribution to quantum computing's impact on statistical mechanics focuses on the development of spin qubit technology. Their approach involves using silicon-based qubits, which leverage existing semiconductor manufacturing processes [7]. Intel has made progress in creating quantum dots that can trap individual electrons, allowing for the manipulation of electron spins as qubits. This technology has potential applications in simulating quantum spin systems, which are fundamental to many statistical mechanical models. Intel has also been working on cryogenic control chips to manage qubit operations at extremely low temperatures, which is crucial for maintaining quantum coherence in statistical mechanical simulations [8].
Strengths: Leveraging existing semiconductor manufacturing expertise, potential for scalable qubit production. Weaknesses: Relatively new entrant in the quantum computing field, still in early stages of quantum hardware development.
Google LLC
Technical Solution: Google's approach to quantum computing's impact on statistical mechanics centers around their Sycamore processor and quantum supremacy experiments. They have demonstrated the ability to perform quantum simulations that are intractable for classical supercomputers, particularly in the realm of quantum many-body physics [4]. Google's quantum processors have been used to simulate dynamical phase transitions and to study the thermalization of quantum systems, providing new insights into fundamental questions in statistical mechanics [5]. Additionally, Google has developed quantum algorithms for sampling from Gibbs distributions, which are crucial in statistical mechanics for describing systems in thermal equilibrium [6].
Strengths: Advanced quantum hardware with demonstrated quantum supremacy, strong focus on quantum algorithms. Weaknesses: Limited qubit coherence times and the need for more robust error correction methods.
Breakthrough Quantum Techniques in Statistical Physics
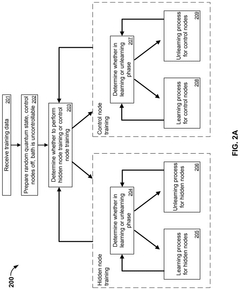
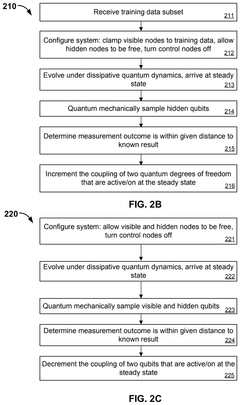
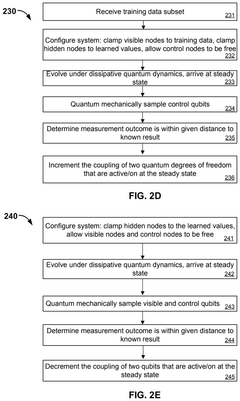
Quantum calculating thermalization rate and boltzmann sampling
PatentPendingUS20230206100A1
Innovation
- Employing quantum computing to map classical problems, like the Fokker-Planck equation, onto quantum operators, allowing for quantum computations that determine thermalization rates and reaction constants more efficiently using supersymmetric Hamiltonians and quantum phase estimation.
Quantum statistic machine
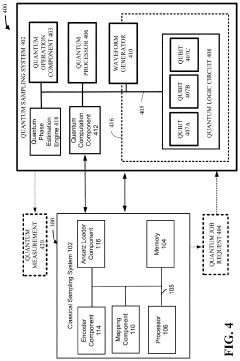
PatentPendingUS20250139489A1
Innovation
- The development of a Quantum Statistic Machine (QSM) that exploits dissipative quantum dynamical maps to solve hard optimization and inference tasks without requiring extreme quantum error correction, using a programmable non-equilibrium ergodic open quantum Markov chain with a unique attracting steady state.
Quantum Error Correction in Statistical Applications
Quantum error correction plays a crucial role in the application of quantum computing to statistical mechanics. As quantum systems are inherently susceptible to noise and decoherence, error correction techniques are essential for maintaining the integrity of quantum computations in statistical applications. These techniques aim to protect quantum information from environmental disturbances and operational imperfections, ensuring the reliability of quantum simulations and calculations in statistical mechanics.
One of the primary challenges in quantum error correction for statistical applications is the need to balance the overhead of error correction with the computational advantages of quantum systems. Traditional error correction codes, such as the surface code, can require a significant number of physical qubits to encode a single logical qubit. This overhead can limit the scalability of quantum simulations for complex statistical systems. However, recent advancements in tailored error correction schemes for specific statistical applications have shown promise in reducing this overhead while maintaining error suppression capabilities.
The development of fault-tolerant quantum circuits is another critical aspect of quantum error correction in statistical mechanics. These circuits are designed to prevent the propagation of errors during quantum operations, which is particularly important for long-running simulations of statistical systems. Fault-tolerant implementations of key statistical algorithms, such as quantum Monte Carlo methods and quantum annealing, have been proposed and are actively being refined to improve their robustness against errors.
Quantum error mitigation techniques, which aim to reduce the impact of errors without full error correction, have gained traction in statistical applications. These techniques, including zero-noise extrapolation and probabilistic error cancellation, can be particularly useful for near-term quantum devices with limited qubit counts and coherence times. By employing these methods, researchers can extract meaningful statistical results from noisy quantum hardware, bridging the gap between current technology and fully error-corrected quantum systems.
The intersection of quantum error correction and machine learning has opened new avenues for improving statistical applications on quantum computers. Machine learning algorithms can be used to optimize error correction protocols, adapting them to the specific noise profiles of quantum hardware and the requirements of statistical simulations. This adaptive approach allows for more efficient use of quantum resources and potentially extends the range of statistical problems that can be tackled with quantum advantage.
As quantum hardware continues to advance, the integration of error correction techniques into statistical mechanics applications is expected to become more seamless. This integration will likely lead to more accurate quantum simulations of complex statistical systems, enabling researchers to explore phenomena that are currently intractable with classical computing methods. The ongoing development of quantum error correction strategies tailored for statistical applications promises to unlock the full potential of quantum computing in this field, potentially revolutionizing our understanding of statistical mechanics and its applications across various scientific disciplines.
One of the primary challenges in quantum error correction for statistical applications is the need to balance the overhead of error correction with the computational advantages of quantum systems. Traditional error correction codes, such as the surface code, can require a significant number of physical qubits to encode a single logical qubit. This overhead can limit the scalability of quantum simulations for complex statistical systems. However, recent advancements in tailored error correction schemes for specific statistical applications have shown promise in reducing this overhead while maintaining error suppression capabilities.
The development of fault-tolerant quantum circuits is another critical aspect of quantum error correction in statistical mechanics. These circuits are designed to prevent the propagation of errors during quantum operations, which is particularly important for long-running simulations of statistical systems. Fault-tolerant implementations of key statistical algorithms, such as quantum Monte Carlo methods and quantum annealing, have been proposed and are actively being refined to improve their robustness against errors.
Quantum error mitigation techniques, which aim to reduce the impact of errors without full error correction, have gained traction in statistical applications. These techniques, including zero-noise extrapolation and probabilistic error cancellation, can be particularly useful for near-term quantum devices with limited qubit counts and coherence times. By employing these methods, researchers can extract meaningful statistical results from noisy quantum hardware, bridging the gap between current technology and fully error-corrected quantum systems.
The intersection of quantum error correction and machine learning has opened new avenues for improving statistical applications on quantum computers. Machine learning algorithms can be used to optimize error correction protocols, adapting them to the specific noise profiles of quantum hardware and the requirements of statistical simulations. This adaptive approach allows for more efficient use of quantum resources and potentially extends the range of statistical problems that can be tackled with quantum advantage.
As quantum hardware continues to advance, the integration of error correction techniques into statistical mechanics applications is expected to become more seamless. This integration will likely lead to more accurate quantum simulations of complex statistical systems, enabling researchers to explore phenomena that are currently intractable with classical computing methods. The ongoing development of quantum error correction strategies tailored for statistical applications promises to unlock the full potential of quantum computing in this field, potentially revolutionizing our understanding of statistical mechanics and its applications across various scientific disciplines.
Ethical Implications of Quantum-Enhanced Statistical Models
The integration of quantum computing with statistical mechanics introduces profound ethical considerations that extend beyond the realm of scientific advancement. As quantum-enhanced statistical models become increasingly sophisticated, they have the potential to revolutionize our understanding of complex systems and enable unprecedented predictive capabilities. However, this power comes with significant ethical implications that must be carefully examined and addressed.
One of the primary ethical concerns is the potential for quantum-enhanced statistical models to exacerbate existing societal inequalities. These advanced models may provide disproportionate advantages to those with access to quantum computing resources, potentially widening the gap between technologically advanced nations and developing countries. This disparity could lead to unequal economic opportunities and further concentrate power in the hands of a select few.
Privacy and data protection present another critical ethical challenge. Quantum-enhanced statistical models may be capable of extracting sensitive information from seemingly innocuous data sets, potentially compromising individual privacy on an unprecedented scale. The ability to process and analyze vast amounts of data with quantum speed raises questions about the boundaries of data ownership and the ethical use of personal information.
The potential for quantum-enhanced statistical models to influence decision-making processes in various fields, such as finance, healthcare, and criminal justice, also raises ethical concerns. While these models may offer more accurate predictions and insights, there is a risk of over-reliance on algorithmic decision-making, potentially diminishing human judgment and accountability. This could lead to unintended biases and discriminatory outcomes, particularly if the underlying data or algorithms are not carefully scrutinized for fairness and inclusivity.
Furthermore, the use of quantum-enhanced statistical models in scientific research and discovery poses ethical questions regarding the nature of scientific inquiry itself. As these models become more powerful, they may be able to generate hypotheses and draw conclusions at a rate that outpaces human comprehension. This raises concerns about the role of human intuition and creativity in scientific discovery, as well as the potential for these models to perpetuate or amplify existing biases in scientific research.
The dual-use nature of quantum-enhanced statistical models also presents ethical challenges. While these technologies have the potential to solve complex problems and advance human knowledge, they could also be used for malicious purposes, such as developing more sophisticated cyberattacks or creating highly targeted disinformation campaigns. Balancing the benefits of scientific progress with the need for responsible development and use of these technologies is a critical ethical consideration.
One of the primary ethical concerns is the potential for quantum-enhanced statistical models to exacerbate existing societal inequalities. These advanced models may provide disproportionate advantages to those with access to quantum computing resources, potentially widening the gap between technologically advanced nations and developing countries. This disparity could lead to unequal economic opportunities and further concentrate power in the hands of a select few.
Privacy and data protection present another critical ethical challenge. Quantum-enhanced statistical models may be capable of extracting sensitive information from seemingly innocuous data sets, potentially compromising individual privacy on an unprecedented scale. The ability to process and analyze vast amounts of data with quantum speed raises questions about the boundaries of data ownership and the ethical use of personal information.
The potential for quantum-enhanced statistical models to influence decision-making processes in various fields, such as finance, healthcare, and criminal justice, also raises ethical concerns. While these models may offer more accurate predictions and insights, there is a risk of over-reliance on algorithmic decision-making, potentially diminishing human judgment and accountability. This could lead to unintended biases and discriminatory outcomes, particularly if the underlying data or algorithms are not carefully scrutinized for fairness and inclusivity.
Furthermore, the use of quantum-enhanced statistical models in scientific research and discovery poses ethical questions regarding the nature of scientific inquiry itself. As these models become more powerful, they may be able to generate hypotheses and draw conclusions at a rate that outpaces human comprehension. This raises concerns about the role of human intuition and creativity in scientific discovery, as well as the potential for these models to perpetuate or amplify existing biases in scientific research.
The dual-use nature of quantum-enhanced statistical models also presents ethical challenges. While these technologies have the potential to solve complex problems and advance human knowledge, they could also be used for malicious purposes, such as developing more sophisticated cyberattacks or creating highly targeted disinformation campaigns. Balancing the benefits of scientific progress with the need for responsible development and use of these technologies is a critical ethical consideration.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!