High Pass Filters in Reinforcement Learning Environments for Hyper-Parameter Tuning
JUL 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
RL HPF Background
Reinforcement Learning (RL) has emerged as a powerful paradigm in machine learning, enabling agents to learn optimal behaviors through interaction with their environment. As RL applications become increasingly complex, the challenge of efficiently tuning hyperparameters has grown in importance. High Pass Filters (HPFs) have recently gained attention as a promising approach to address this challenge in RL environments.
The concept of HPFs in RL draws inspiration from signal processing, where they are used to attenuate low-frequency components while allowing high-frequency components to pass through. In the context of RL, HPFs can be applied to various aspects of the learning process, including reward shaping, state representation, and policy updates.
The primary motivation behind incorporating HPFs in RL environments is to enhance the learning efficiency and stability of agents. Traditional RL algorithms often struggle with long-term dependencies and sparse rewards, leading to slow convergence and suboptimal performance. By filtering out low-frequency noise and emphasizing high-frequency signals, HPFs can help agents focus on more relevant information and accelerate the learning process.
One of the key applications of HPFs in RL is in the domain of hyperparameter tuning. Hyperparameters play a crucial role in determining the performance of RL algorithms, but finding optimal values can be a time-consuming and computationally expensive process. HPFs offer a potential solution by allowing for more efficient exploration of the hyperparameter space.
The integration of HPFs into RL environments for hyperparameter tuning has its roots in adaptive control theory and optimization techniques. Early work in this area focused on using frequency-domain analysis to improve the stability and convergence properties of RL algorithms. As the field progressed, researchers began to explore more sophisticated filtering techniques and their applications to various RL tasks.
Recent advancements in deep learning and neural network architectures have further expanded the potential of HPFs in RL. Deep RL models can now incorporate learnable filters as part of their network structure, allowing for adaptive filtering that evolves alongside the agent's policy. This approach has shown promise in improving sample efficiency and generalization across different tasks and environments.
As the field of RL continues to evolve, the role of HPFs in hyperparameter tuning is likely to become increasingly important. Researchers are exploring novel ways to combine HPFs with other advanced techniques, such as meta-learning and multi-task learning, to create more robust and adaptable RL systems. The ongoing development of HPF-based approaches promises to unlock new possibilities in the design and optimization of RL algorithms, paving the way for more efficient and effective learning in complex, real-world applications.
The concept of HPFs in RL draws inspiration from signal processing, where they are used to attenuate low-frequency components while allowing high-frequency components to pass through. In the context of RL, HPFs can be applied to various aspects of the learning process, including reward shaping, state representation, and policy updates.
The primary motivation behind incorporating HPFs in RL environments is to enhance the learning efficiency and stability of agents. Traditional RL algorithms often struggle with long-term dependencies and sparse rewards, leading to slow convergence and suboptimal performance. By filtering out low-frequency noise and emphasizing high-frequency signals, HPFs can help agents focus on more relevant information and accelerate the learning process.
One of the key applications of HPFs in RL is in the domain of hyperparameter tuning. Hyperparameters play a crucial role in determining the performance of RL algorithms, but finding optimal values can be a time-consuming and computationally expensive process. HPFs offer a potential solution by allowing for more efficient exploration of the hyperparameter space.
The integration of HPFs into RL environments for hyperparameter tuning has its roots in adaptive control theory and optimization techniques. Early work in this area focused on using frequency-domain analysis to improve the stability and convergence properties of RL algorithms. As the field progressed, researchers began to explore more sophisticated filtering techniques and their applications to various RL tasks.
Recent advancements in deep learning and neural network architectures have further expanded the potential of HPFs in RL. Deep RL models can now incorporate learnable filters as part of their network structure, allowing for adaptive filtering that evolves alongside the agent's policy. This approach has shown promise in improving sample efficiency and generalization across different tasks and environments.
As the field of RL continues to evolve, the role of HPFs in hyperparameter tuning is likely to become increasingly important. Researchers are exploring novel ways to combine HPFs with other advanced techniques, such as meta-learning and multi-task learning, to create more robust and adaptable RL systems. The ongoing development of HPF-based approaches promises to unlock new possibilities in the design and optimization of RL algorithms, paving the way for more efficient and effective learning in complex, real-world applications.
Market Demand Analysis
The market demand for high pass filters in reinforcement learning environments for hyper-parameter tuning has been steadily increasing in recent years. This growth is primarily driven by the expanding applications of reinforcement learning across various industries and the growing complexity of machine learning models.
In the field of artificial intelligence and machine learning, reinforcement learning has gained significant traction due to its ability to solve complex decision-making problems. As the complexity of these problems increases, so does the need for efficient hyper-parameter tuning methods. High pass filters have emerged as a valuable tool in this context, offering a way to optimize the learning process and improve model performance.
The financial sector has shown particular interest in this technology, with major banks and hedge funds investing heavily in reinforcement learning systems for algorithmic trading. These institutions require precise hyper-parameter tuning to maximize their trading strategies' effectiveness, creating a substantial market for high pass filter solutions.
Similarly, the automotive industry has been adopting reinforcement learning for autonomous driving systems. The need for robust and efficient hyper-parameter tuning in this safety-critical application has further fueled the demand for advanced filtering techniques.
The healthcare sector is another significant market driver, with reinforcement learning being applied to personalized treatment plans and drug discovery processes. The ability to fine-tune these models efficiently can lead to more accurate predictions and better patient outcomes, making high pass filters an attractive solution for healthcare AI developers.
In the robotics industry, reinforcement learning is used to train robots for complex tasks in manufacturing and logistics. The demand for high pass filters in this sector is driven by the need to optimize robot behavior quickly and efficiently, reducing training time and improving overall performance.
Market analysts predict that the global market for reinforcement learning, including tools for hyper-parameter tuning, will continue to grow at a compound annual growth rate of over 50% in the next five years. This growth is expected to be particularly strong in North America and Asia-Pacific regions, where investments in AI research and development are highest.
As the demand for more sophisticated reinforcement learning models grows, so does the need for advanced hyper-parameter tuning techniques. High pass filters are well-positioned to meet this demand, offering a powerful tool for researchers and developers to optimize their models and achieve better results across a wide range of applications.
In the field of artificial intelligence and machine learning, reinforcement learning has gained significant traction due to its ability to solve complex decision-making problems. As the complexity of these problems increases, so does the need for efficient hyper-parameter tuning methods. High pass filters have emerged as a valuable tool in this context, offering a way to optimize the learning process and improve model performance.
The financial sector has shown particular interest in this technology, with major banks and hedge funds investing heavily in reinforcement learning systems for algorithmic trading. These institutions require precise hyper-parameter tuning to maximize their trading strategies' effectiveness, creating a substantial market for high pass filter solutions.
Similarly, the automotive industry has been adopting reinforcement learning for autonomous driving systems. The need for robust and efficient hyper-parameter tuning in this safety-critical application has further fueled the demand for advanced filtering techniques.
The healthcare sector is another significant market driver, with reinforcement learning being applied to personalized treatment plans and drug discovery processes. The ability to fine-tune these models efficiently can lead to more accurate predictions and better patient outcomes, making high pass filters an attractive solution for healthcare AI developers.
In the robotics industry, reinforcement learning is used to train robots for complex tasks in manufacturing and logistics. The demand for high pass filters in this sector is driven by the need to optimize robot behavior quickly and efficiently, reducing training time and improving overall performance.
Market analysts predict that the global market for reinforcement learning, including tools for hyper-parameter tuning, will continue to grow at a compound annual growth rate of over 50% in the next five years. This growth is expected to be particularly strong in North America and Asia-Pacific regions, where investments in AI research and development are highest.
As the demand for more sophisticated reinforcement learning models grows, so does the need for advanced hyper-parameter tuning techniques. High pass filters are well-positioned to meet this demand, offering a powerful tool for researchers and developers to optimize their models and achieve better results across a wide range of applications.
HPF Challenges in RL
The integration of High Pass Filters (HPFs) in Reinforcement Learning (RL) environments for hyper-parameter tuning presents several significant challenges. One of the primary obstacles is the inherent complexity of RL systems, which often involve multiple interacting components and non-linear dynamics. HPFs, designed to attenuate low-frequency signals while allowing high-frequency signals to pass, must be carefully implemented to avoid disrupting the delicate balance of the RL process.
A key challenge lies in determining the appropriate cutoff frequency for the HPF. In RL environments, the distinction between "noise" and valuable information is not always clear-cut. Setting the cutoff too high may filter out important low-frequency patterns that are crucial for learning optimal policies. Conversely, a cutoff that is too low may fail to adequately remove unwanted noise, potentially leading to instability in the learning process.
Another significant hurdle is the dynamic nature of RL environments. As the agent learns and adapts, the characteristics of the input signals may change over time. This temporal variability makes it difficult to design a static HPF that remains effective throughout the entire learning process. Adaptive filtering techniques may be necessary, but implementing these in a way that doesn't introduce additional instability or computational overhead is a complex task.
The curse of dimensionality poses yet another challenge when applying HPFs in RL. Many RL problems involve high-dimensional state spaces, and applying filters across all dimensions simultaneously can be computationally expensive. Moreover, different dimensions may require different filtering approaches, necessitating a more sophisticated, multi-dimensional filtering strategy.
Integrating HPFs with existing RL algorithms presents its own set of challenges. Many popular RL methods, such as Q-learning or policy gradient algorithms, are not inherently designed to work with filtered inputs. Modifying these algorithms to incorporate HPFs while maintaining their theoretical guarantees and convergence properties requires careful consideration and potentially significant algorithmic adjustments.
The impact of HPFs on exploration-exploitation trade-offs in RL is another area of concern. Filtering may inadvertently affect the agent's ability to explore its environment effectively, potentially leading to premature convergence to suboptimal policies. Balancing the benefits of noise reduction with the need for sufficient exploration is a delicate task that requires fine-tuning and extensive experimentation.
Lastly, the challenge of interpretability arises when using HPFs in RL. Understanding how the filtered signals influence the learning process and decision-making of the agent can be difficult, especially in complex environments. This lack of transparency may hinder debugging efforts and make it challenging to gain insights into the underlying dynamics of the RL system.
A key challenge lies in determining the appropriate cutoff frequency for the HPF. In RL environments, the distinction between "noise" and valuable information is not always clear-cut. Setting the cutoff too high may filter out important low-frequency patterns that are crucial for learning optimal policies. Conversely, a cutoff that is too low may fail to adequately remove unwanted noise, potentially leading to instability in the learning process.
Another significant hurdle is the dynamic nature of RL environments. As the agent learns and adapts, the characteristics of the input signals may change over time. This temporal variability makes it difficult to design a static HPF that remains effective throughout the entire learning process. Adaptive filtering techniques may be necessary, but implementing these in a way that doesn't introduce additional instability or computational overhead is a complex task.
The curse of dimensionality poses yet another challenge when applying HPFs in RL. Many RL problems involve high-dimensional state spaces, and applying filters across all dimensions simultaneously can be computationally expensive. Moreover, different dimensions may require different filtering approaches, necessitating a more sophisticated, multi-dimensional filtering strategy.
Integrating HPFs with existing RL algorithms presents its own set of challenges. Many popular RL methods, such as Q-learning or policy gradient algorithms, are not inherently designed to work with filtered inputs. Modifying these algorithms to incorporate HPFs while maintaining their theoretical guarantees and convergence properties requires careful consideration and potentially significant algorithmic adjustments.
The impact of HPFs on exploration-exploitation trade-offs in RL is another area of concern. Filtering may inadvertently affect the agent's ability to explore its environment effectively, potentially leading to premature convergence to suboptimal policies. Balancing the benefits of noise reduction with the need for sufficient exploration is a delicate task that requires fine-tuning and extensive experimentation.
Lastly, the challenge of interpretability arises when using HPFs in RL. Understanding how the filtered signals influence the learning process and decision-making of the agent can be difficult, especially in complex environments. This lack of transparency may hinder debugging efforts and make it challenging to gain insights into the underlying dynamics of the RL system.
Current HPF Solutions
01 Adaptive filter parameter optimization
Techniques for dynamically adjusting high-pass filter parameters based on input signal characteristics and system requirements. This involves real-time analysis of signal properties and automatic tuning of filter coefficients to optimize performance for varying conditions.- Adaptive filter parameter optimization: Techniques for dynamically adjusting high-pass filter parameters based on input signal characteristics and system requirements. This involves real-time analysis of signal properties and automatic tuning of filter coefficients to optimize performance for varying conditions.
- Machine learning for filter tuning: Application of machine learning algorithms to optimize high-pass filter parameters. These methods use historical data and performance metrics to train models that can predict optimal filter settings for different scenarios, improving overall system efficiency and adaptability.
- Multi-objective optimization for filter design: Approaches that consider multiple performance criteria simultaneously when tuning high-pass filter parameters. This involves balancing trade-offs between different objectives such as passband ripple, stopband attenuation, and phase response to achieve optimal overall performance.
- Frequency-dependent parameter adjustment: Methods for adjusting high-pass filter parameters based on the frequency content of the input signal. This approach allows for more precise filtering by adapting the filter characteristics to match the spectral properties of the signal being processed.
- Hardware-efficient implementation of tunable filters: Techniques for implementing high-pass filters with tunable parameters in hardware-efficient ways. This includes optimizing digital filter structures, using lookup tables for coefficient storage, and employing efficient parameter update mechanisms to reduce computational complexity and power consumption.
02 Machine learning for filter tuning
Application of machine learning algorithms to optimize high-pass filter parameters. These methods use historical data and performance metrics to train models that can predict optimal filter settings for different scenarios, improving overall system efficiency and adaptability.Expand Specific Solutions03 Frequency domain analysis for parameter selection
Utilization of frequency domain analysis techniques to inform high-pass filter parameter selection. This approach involves examining the spectral content of signals to determine appropriate cutoff frequencies and filter orders, ensuring effective noise reduction while preserving desired signal components.Expand Specific Solutions04 Multi-objective optimization for filter design
Implementation of multi-objective optimization algorithms to balance conflicting requirements in high-pass filter design. This method considers multiple performance criteria simultaneously, such as passband ripple, stopband attenuation, and phase response, to find optimal filter parameters that satisfy diverse system needs.Expand Specific Solutions05 Adaptive noise cancellation in high-pass filters
Integration of adaptive noise cancellation techniques with high-pass filtering to enhance signal quality. This approach dynamically estimates and removes noise components, allowing for more precise tuning of filter parameters to isolate desired signal characteristics in challenging environments.Expand Specific Solutions
Key RL HPF Players
The competitive landscape for High Pass Filters in Reinforcement Learning Environments for Hyper-Parameter Tuning is in an early growth stage, with increasing market size as AI and machine learning applications expand. The technology is moderately mature, with ongoing refinements. Key players like Google, Microsoft, and IBM are leading research and development efforts, leveraging their extensive AI capabilities. Emerging companies such as DeepMind and NVIDIA are also making significant contributions, focusing on specialized applications and hardware optimizations. The field is characterized by rapid innovation and collaboration between academia and industry, with universities like South China University of Technology actively participating in advancing the technology.
Microsoft Technology Licensing LLC
Technical Solution: Microsoft has developed an innovative approach to high-pass filtering in reinforcement learning for hyper-parameter tuning, focusing on robustness and generalization. Their method employs a multi-agent system where each agent uses a different high-pass filter configuration, allowing for diverse exploration strategies[2]. The system uses a novel ensemble learning technique to combine the insights from these agents, resulting in more stable and generalizable hyper-parameter estimates. Microsoft has also incorporated this filtering approach into their Azure Machine Learning platform, providing easy access to these advanced techniques for a wide range of users[4]. Additionally, they have developed a set of adaptive regularization techniques that work in conjunction with the high-pass filters to prevent overfitting in complex RL environments[6].
Strengths: Robust performance across diverse environments, easy integration with cloud-based ML platforms. Weaknesses: May have higher computational overhead due to multi-agent approach.
Google LLC
Technical Solution: Google has developed an advanced approach to high-pass filters in reinforcement learning for hyper-parameter tuning. Their method utilizes a combination of spectral analysis and adaptive filtering techniques to dynamically adjust the cut-off frequency of the high-pass filter based on the learning progress[1]. This allows for more efficient exploration of the parameter space by filtering out low-frequency noise while preserving important high-frequency components. The system employs a multi-scale architecture that applies different filter configurations at various stages of the learning process, enabling fine-grained control over the information flow[3]. Additionally, Google has integrated this filtering approach with their TensorFlow framework, allowing for seamless implementation in large-scale machine learning pipelines[5].
Strengths: Highly adaptive and scalable, seamless integration with existing ML frameworks. Weaknesses: May require significant computational resources for complex environments.
Core HPF Innovations
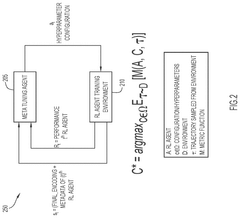
Reinforcement machine learning with hyperparameter tuning
PatentPendingUS20240428084A1
Innovation
- A meta-hyperparameter tuning system that learns from prior experiences to recommend effective initial hyperparameters and dynamically tune them during training, using a meta-tuning agent trained on historical data to predict hyperparameters based on the current state of the RL agent and environment.
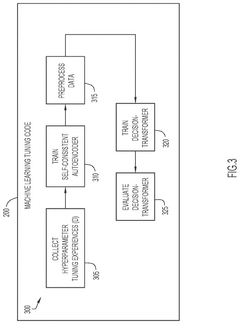
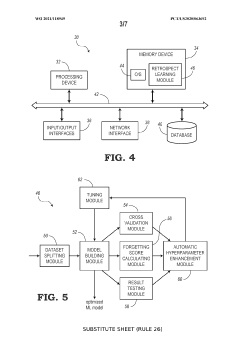
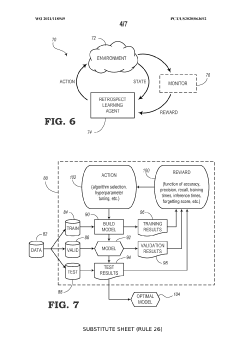
Adaptive learning system utilizing reinforcement learning to tune hyperparameters in machine learning techniques
PatentWO2021118949A2
Innovation
- An adaptive learning system utilizing reinforcement learning to automatically tune hyperparameters, leveraging a retrospect learning module that defines states, actions, and rewards to optimize hyperparameter settings, reducing training time and data requirements while maximizing knowledge retention and accuracy.
RL HPF Benchmarking
Benchmarking high pass filters (HPFs) in reinforcement learning (RL) environments for hyper-parameter tuning is a critical process that evaluates the effectiveness of HPFs in optimizing RL algorithms. This benchmarking process involves a systematic comparison of different HPF configurations and their impact on the performance of RL agents across various tasks and environments.
The benchmarking process typically begins with the selection of a diverse set of RL environments that represent different challenges and complexities. These environments may include classic control problems, robotics simulations, and game-based scenarios. The diversity ensures that the benchmarking results are generalizable across different domains.
Next, a range of HPF configurations is defined, varying parameters such as cutoff frequency, filter order, and implementation method. These configurations are then applied to the RL algorithms under study, which may include popular methods like Deep Q-Networks (DQN), Proximal Policy Optimization (PPO), or Soft Actor-Critic (SAC).
The performance metrics for benchmarking typically include learning speed, final performance, stability, and sample efficiency. These metrics are measured over multiple runs to account for the stochastic nature of RL algorithms. The benchmarking process also considers the computational overhead introduced by the HPFs, as this can impact the practical applicability of the approach.
To ensure fair comparisons, the benchmarking process employs standardized evaluation protocols. This includes using fixed random seeds, consistent hardware configurations, and identical training durations across all experiments. The results are often presented using learning curves, which show the agent's performance over time, as well as summary statistics that capture key performance indicators.
Advanced benchmarking approaches may also incorporate sensitivity analysis to understand how small changes in HPF parameters affect RL performance. This can provide insights into the robustness of different HPF configurations and guide the selection of optimal settings for specific RL tasks.
The benchmarking results are typically analyzed to identify patterns and trends in the effectiveness of HPFs across different environments and RL algorithms. This analysis may reveal which HPF configurations work best for certain types of tasks or which RL algorithms benefit most from the application of HPFs.
Ultimately, the goal of RL HPF benchmarking is to provide practitioners with empirical evidence to guide the selection and implementation of HPFs in their RL systems. The insights gained from this process can lead to more efficient hyper-parameter tuning strategies and improved overall performance of RL agents in real-world applications.
The benchmarking process typically begins with the selection of a diverse set of RL environments that represent different challenges and complexities. These environments may include classic control problems, robotics simulations, and game-based scenarios. The diversity ensures that the benchmarking results are generalizable across different domains.
Next, a range of HPF configurations is defined, varying parameters such as cutoff frequency, filter order, and implementation method. These configurations are then applied to the RL algorithms under study, which may include popular methods like Deep Q-Networks (DQN), Proximal Policy Optimization (PPO), or Soft Actor-Critic (SAC).
The performance metrics for benchmarking typically include learning speed, final performance, stability, and sample efficiency. These metrics are measured over multiple runs to account for the stochastic nature of RL algorithms. The benchmarking process also considers the computational overhead introduced by the HPFs, as this can impact the practical applicability of the approach.
To ensure fair comparisons, the benchmarking process employs standardized evaluation protocols. This includes using fixed random seeds, consistent hardware configurations, and identical training durations across all experiments. The results are often presented using learning curves, which show the agent's performance over time, as well as summary statistics that capture key performance indicators.
Advanced benchmarking approaches may also incorporate sensitivity analysis to understand how small changes in HPF parameters affect RL performance. This can provide insights into the robustness of different HPF configurations and guide the selection of optimal settings for specific RL tasks.
The benchmarking results are typically analyzed to identify patterns and trends in the effectiveness of HPFs across different environments and RL algorithms. This analysis may reveal which HPF configurations work best for certain types of tasks or which RL algorithms benefit most from the application of HPFs.
Ultimately, the goal of RL HPF benchmarking is to provide practitioners with empirical evidence to guide the selection and implementation of HPFs in their RL systems. The insights gained from this process can lead to more efficient hyper-parameter tuning strategies and improved overall performance of RL agents in real-world applications.
HPF Scalability in RL
The scalability of High Pass Filters (HPFs) in Reinforcement Learning (RL) environments presents both challenges and opportunities for hyper-parameter tuning. As RL systems become increasingly complex and are applied to larger-scale problems, the ability to efficiently tune hyper-parameters becomes crucial for achieving optimal performance. HPFs, when implemented in RL environments, can significantly impact the scalability of the learning process.
One of the primary considerations for HPF scalability in RL is the computational overhead introduced by the filtering process. As the dimensionality of the state space increases, the computational cost of applying HPFs to each state representation grows exponentially. This can lead to bottlenecks in the learning process, particularly in high-dimensional environments or when dealing with large datasets.
To address this challenge, researchers have explored various techniques to improve the scalability of HPFs in RL. One approach involves the use of sparse representations and efficient data structures to reduce the memory footprint and computational complexity of the filtering process. By leveraging techniques such as sparse matrices or hash-based data structures, it becomes possible to apply HPFs to larger state spaces without incurring prohibitive computational costs.
Another important aspect of HPF scalability in RL is the ability to adapt the filter parameters dynamically during the learning process. As the agent explores the environment and accumulates experience, the optimal filter parameters may change over time. Implementing adaptive HPFs that can adjust their cutoff frequencies or filter coefficients based on the current state of the learning process can significantly enhance the scalability and effectiveness of the approach.
The integration of HPFs with distributed and parallel computing architectures presents another avenue for improving scalability. By leveraging multi-core processors or distributed computing clusters, it becomes possible to parallelize the filtering process across multiple computational units. This approach can significantly reduce the overall computation time and enable the application of HPFs to larger-scale RL problems.
Furthermore, the scalability of HPFs in RL environments is closely tied to the choice of learning algorithms and policy representations. Certain RL algorithms, such as those based on function approximation or deep neural networks, may be more amenable to efficient integration with HPFs. Exploring the synergies between different RL algorithms and HPF implementations can lead to more scalable and effective hyper-parameter tuning approaches.
As the field of RL continues to evolve, addressing the scalability challenges associated with HPFs remains an active area of research. Future developments in this area may involve the exploration of novel filtering techniques, the integration of HPFs with advanced optimization algorithms, and the development of specialized hardware accelerators designed to efficiently implement HPFs in RL environments.
One of the primary considerations for HPF scalability in RL is the computational overhead introduced by the filtering process. As the dimensionality of the state space increases, the computational cost of applying HPFs to each state representation grows exponentially. This can lead to bottlenecks in the learning process, particularly in high-dimensional environments or when dealing with large datasets.
To address this challenge, researchers have explored various techniques to improve the scalability of HPFs in RL. One approach involves the use of sparse representations and efficient data structures to reduce the memory footprint and computational complexity of the filtering process. By leveraging techniques such as sparse matrices or hash-based data structures, it becomes possible to apply HPFs to larger state spaces without incurring prohibitive computational costs.
Another important aspect of HPF scalability in RL is the ability to adapt the filter parameters dynamically during the learning process. As the agent explores the environment and accumulates experience, the optimal filter parameters may change over time. Implementing adaptive HPFs that can adjust their cutoff frequencies or filter coefficients based on the current state of the learning process can significantly enhance the scalability and effectiveness of the approach.
The integration of HPFs with distributed and parallel computing architectures presents another avenue for improving scalability. By leveraging multi-core processors or distributed computing clusters, it becomes possible to parallelize the filtering process across multiple computational units. This approach can significantly reduce the overall computation time and enable the application of HPFs to larger-scale RL problems.
Furthermore, the scalability of HPFs in RL environments is closely tied to the choice of learning algorithms and policy representations. Certain RL algorithms, such as those based on function approximation or deep neural networks, may be more amenable to efficient integration with HPFs. Exploring the synergies between different RL algorithms and HPF implementations can lead to more scalable and effective hyper-parameter tuning approaches.
As the field of RL continues to evolve, addressing the scalability challenges associated with HPFs remains an active area of research. Future developments in this area may involve the exploration of novel filtering techniques, the integration of HPFs with advanced optimization algorithms, and the development of specialized hardware accelerators designed to efficiently implement HPFs in RL environments.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!