Evaluating Quantum Mechanical Models in Quantum Computing Tasks
SEP 5, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Quantum Computing Evolution and Research Objectives
Quantum computing has evolved significantly since its theoretical conception in the early 1980s by Richard Feynman and others who recognized the potential of quantum mechanics to solve computational problems beyond the reach of classical computers. The field has progressed through several distinct phases, beginning with theoretical foundations, followed by the development of quantum algorithms such as Shor's and Grover's in the 1990s, and more recently, the creation of physical quantum computing systems with increasing qubit counts and coherence times.
The evolution of quantum mechanical models within quantum computing has been particularly noteworthy. Early models focused primarily on quantum circuit models and quantum Turing machines, providing theoretical frameworks for understanding quantum computation. As the field matured, alternative models emerged, including adiabatic quantum computing, topological quantum computing, and measurement-based quantum computing, each offering unique approaches to harnessing quantum phenomena for computational advantage.
Recent years have witnessed significant advancements in quantum error correction and fault-tolerant quantum computing, addressing one of the field's most persistent challenges: quantum decoherence. The development of surface codes and other error correction techniques has brought the field closer to achieving practical quantum advantage in real-world applications.
The current research landscape is characterized by a dual focus on near-term applications using Noisy Intermediate-Scale Quantum (NISQ) devices and long-term goals of building fault-tolerant universal quantum computers. This bifurcation reflects the pragmatic recognition that while fully error-corrected quantum computers remain years away, existing quantum systems can potentially offer advantages in specific domains.
Research objectives in quantum mechanical model evaluation center around several key areas. First, developing robust benchmarking methodologies to accurately assess the performance of different quantum mechanical models across various computational tasks. Second, establishing standardized metrics for comparing quantum algorithms and hardware implementations. Third, identifying application-specific quantum mechanical models that may offer advantages for particular problem domains such as quantum chemistry, optimization, or machine learning.
Another critical research objective involves bridging the gap between theoretical quantum mechanical models and their physical implementations. This includes developing more accurate noise models, improving quantum control techniques, and creating more efficient methods for mapping abstract quantum algorithms onto physical quantum architectures with specific connectivity constraints and error characteristics.
The ultimate goal of this research direction is to establish a comprehensive framework for evaluating quantum mechanical models that can guide both theoretical development and practical implementation decisions, accelerating progress toward quantum computational advantage in commercially relevant applications.
The evolution of quantum mechanical models within quantum computing has been particularly noteworthy. Early models focused primarily on quantum circuit models and quantum Turing machines, providing theoretical frameworks for understanding quantum computation. As the field matured, alternative models emerged, including adiabatic quantum computing, topological quantum computing, and measurement-based quantum computing, each offering unique approaches to harnessing quantum phenomena for computational advantage.
Recent years have witnessed significant advancements in quantum error correction and fault-tolerant quantum computing, addressing one of the field's most persistent challenges: quantum decoherence. The development of surface codes and other error correction techniques has brought the field closer to achieving practical quantum advantage in real-world applications.
The current research landscape is characterized by a dual focus on near-term applications using Noisy Intermediate-Scale Quantum (NISQ) devices and long-term goals of building fault-tolerant universal quantum computers. This bifurcation reflects the pragmatic recognition that while fully error-corrected quantum computers remain years away, existing quantum systems can potentially offer advantages in specific domains.
Research objectives in quantum mechanical model evaluation center around several key areas. First, developing robust benchmarking methodologies to accurately assess the performance of different quantum mechanical models across various computational tasks. Second, establishing standardized metrics for comparing quantum algorithms and hardware implementations. Third, identifying application-specific quantum mechanical models that may offer advantages for particular problem domains such as quantum chemistry, optimization, or machine learning.
Another critical research objective involves bridging the gap between theoretical quantum mechanical models and their physical implementations. This includes developing more accurate noise models, improving quantum control techniques, and creating more efficient methods for mapping abstract quantum algorithms onto physical quantum architectures with specific connectivity constraints and error characteristics.
The ultimate goal of this research direction is to establish a comprehensive framework for evaluating quantum mechanical models that can guide both theoretical development and practical implementation decisions, accelerating progress toward quantum computational advantage in commercially relevant applications.
Market Analysis for Quantum Computing Applications
The quantum computing market is experiencing unprecedented growth, with projections indicating a market value reaching $1.7 billion by 2026, growing at a CAGR of approximately 30.2% from 2021. This growth is primarily driven by increasing investments from both public and private sectors, recognizing the transformative potential of quantum technologies across various industries.
Financial services represent one of the most promising application areas, with quantum computing offering significant advantages in portfolio optimization, risk assessment, and fraud detection. Major financial institutions including JPMorgan Chase, Goldman Sachs, and Barclays have established dedicated quantum computing research teams to explore these applications.
The pharmaceutical and healthcare sectors are also rapidly adopting quantum computing solutions, particularly for drug discovery and molecular modeling processes. Companies like Roche, Biogen, and Pfizer are leveraging quantum algorithms to simulate molecular interactions at unprecedented scales, potentially reducing drug development timelines from years to months.
In the logistics and supply chain domain, quantum computing applications are emerging for route optimization, inventory management, and demand forecasting. Organizations such as DHL and FedEx are exploring quantum solutions to solve complex logistics problems that are computationally infeasible for classical computers.
Cybersecurity represents both a challenge and opportunity in the quantum computing landscape. While quantum computers threaten current encryption standards, quantum-resistant cryptography is creating a new market segment estimated to reach $300 million by 2025. Companies like IBM, Microsoft, and Google are actively developing quantum-safe security solutions.
Government and defense sectors are making substantial investments in quantum computing research, with the US, China, and EU allocating billions in funding. These investments focus on applications ranging from intelligence analysis to materials science for defense applications.
The market for quantum computing services is currently dominated by cloud-based quantum computing platforms, with IBM Quantum, Amazon Braket, and Microsoft Azure Quantum leading the space. This service model is democratizing access to quantum resources, allowing smaller organizations to experiment without significant capital investment.
Customer adoption patterns reveal a preference for hybrid quantum-classical approaches, with organizations integrating quantum solutions alongside existing high-performance computing infrastructure rather than pursuing complete replacements. This trend is expected to continue as quantum technologies mature and demonstrate more definitive advantages in specific computational tasks.
Financial services represent one of the most promising application areas, with quantum computing offering significant advantages in portfolio optimization, risk assessment, and fraud detection. Major financial institutions including JPMorgan Chase, Goldman Sachs, and Barclays have established dedicated quantum computing research teams to explore these applications.
The pharmaceutical and healthcare sectors are also rapidly adopting quantum computing solutions, particularly for drug discovery and molecular modeling processes. Companies like Roche, Biogen, and Pfizer are leveraging quantum algorithms to simulate molecular interactions at unprecedented scales, potentially reducing drug development timelines from years to months.
In the logistics and supply chain domain, quantum computing applications are emerging for route optimization, inventory management, and demand forecasting. Organizations such as DHL and FedEx are exploring quantum solutions to solve complex logistics problems that are computationally infeasible for classical computers.
Cybersecurity represents both a challenge and opportunity in the quantum computing landscape. While quantum computers threaten current encryption standards, quantum-resistant cryptography is creating a new market segment estimated to reach $300 million by 2025. Companies like IBM, Microsoft, and Google are actively developing quantum-safe security solutions.
Government and defense sectors are making substantial investments in quantum computing research, with the US, China, and EU allocating billions in funding. These investments focus on applications ranging from intelligence analysis to materials science for defense applications.
The market for quantum computing services is currently dominated by cloud-based quantum computing platforms, with IBM Quantum, Amazon Braket, and Microsoft Azure Quantum leading the space. This service model is democratizing access to quantum resources, allowing smaller organizations to experiment without significant capital investment.
Customer adoption patterns reveal a preference for hybrid quantum-classical approaches, with organizations integrating quantum solutions alongside existing high-performance computing infrastructure rather than pursuing complete replacements. This trend is expected to continue as quantum technologies mature and demonstrate more definitive advantages in specific computational tasks.
Current Quantum Mechanical Models: Status and Barriers
The quantum computing landscape is currently dominated by several quantum mechanical models, each with distinct characteristics and limitations. The gate-based quantum computing model, championed by IBM, Google, and Rigetti, represents the most widely researched approach. This model manipulates qubits through quantum gates analogous to classical computing's logic gates, but faces significant challenges in qubit coherence time and gate fidelity. Current state-of-the-art systems can maintain coherence for only microseconds to milliseconds, severely limiting computation complexity.
Adiabatic quantum computing, exemplified by D-Wave Systems, offers an alternative approach focused on quantum annealing to find optimal solutions to optimization problems. While this model has demonstrated capabilities with thousands of qubits, its specialized nature restricts application scope primarily to quadratic unconstrained binary optimization problems. The ongoing debate about whether these systems demonstrate true quantum advantage over classical algorithms remains unresolved.
Topological quantum computing represents a promising theoretical model that could potentially overcome decoherence issues by encoding quantum information in non-local properties of topological states. Microsoft has invested heavily in this approach, but despite theoretical elegance, experimental realization of topological qubits remains elusive, with no functional topological quantum computer yet demonstrated.
Measurement-based quantum computing presents another paradigm where computation proceeds through a sequence of single-qubit measurements on a highly entangled initial state. While theoretically powerful, creating and maintaining the required entangled states poses significant experimental challenges, limiting practical implementation.
A fundamental barrier across all models is the quantum error correction challenge. Quantum states are inherently fragile, requiring sophisticated error correction techniques that demand substantial qubit overhead. Current error rates remain orders of magnitude higher than thresholds required for fault-tolerant quantum computing, necessitating physical qubit counts in the millions to achieve reliable logical qubits.
The scalability barrier represents another critical challenge. While small-scale quantum processors with dozens of qubits exist, scaling to hundreds or thousands of high-quality qubits encounters significant engineering obstacles in wiring, control electronics, and cross-talk mitigation. Additionally, the verification and benchmarking of quantum systems become exponentially more difficult as system size increases, creating a validation gap that complicates progress assessment.
Adiabatic quantum computing, exemplified by D-Wave Systems, offers an alternative approach focused on quantum annealing to find optimal solutions to optimization problems. While this model has demonstrated capabilities with thousands of qubits, its specialized nature restricts application scope primarily to quadratic unconstrained binary optimization problems. The ongoing debate about whether these systems demonstrate true quantum advantage over classical algorithms remains unresolved.
Topological quantum computing represents a promising theoretical model that could potentially overcome decoherence issues by encoding quantum information in non-local properties of topological states. Microsoft has invested heavily in this approach, but despite theoretical elegance, experimental realization of topological qubits remains elusive, with no functional topological quantum computer yet demonstrated.
Measurement-based quantum computing presents another paradigm where computation proceeds through a sequence of single-qubit measurements on a highly entangled initial state. While theoretically powerful, creating and maintaining the required entangled states poses significant experimental challenges, limiting practical implementation.
A fundamental barrier across all models is the quantum error correction challenge. Quantum states are inherently fragile, requiring sophisticated error correction techniques that demand substantial qubit overhead. Current error rates remain orders of magnitude higher than thresholds required for fault-tolerant quantum computing, necessitating physical qubit counts in the millions to achieve reliable logical qubits.
The scalability barrier represents another critical challenge. While small-scale quantum processors with dozens of qubits exist, scaling to hundreds or thousands of high-quality qubits encounters significant engineering obstacles in wiring, control electronics, and cross-talk mitigation. Additionally, the verification and benchmarking of quantum systems become exponentially more difficult as system size increases, creating a validation gap that complicates progress assessment.
Contemporary Quantum Mechanical Modeling Approaches
01 Accuracy and Precision Metrics for Quantum Models
Evaluation metrics for quantum mechanical models often focus on accuracy and precision. These metrics assess how closely the quantum model's predictions match experimental or theoretical benchmarks. Common metrics include mean squared error, root mean squared error, and correlation coefficients. These measurements help quantify the reliability of quantum simulations and their ability to reproduce known quantum phenomena or predict new behaviors accurately.- Accuracy and Precision Metrics for Quantum Models: Various metrics are used to evaluate the accuracy and precision of quantum mechanical models. These metrics include fidelity measures, error rates, and statistical validation techniques that compare predicted quantum states with experimental or theoretical benchmarks. Advanced evaluation frameworks incorporate uncertainty quantification and confidence intervals to assess the reliability of quantum simulations across different problem domains.
- Performance Evaluation in Quantum Computing Applications: Evaluation metrics specific to quantum computing applications focus on computational efficiency, resource utilization, and algorithm performance. These metrics measure quantum speedup, qubit requirements, circuit depth, and execution time compared to classical alternatives. Performance benchmarks are established for various quantum algorithms to assess their practical viability and scalability across different hardware implementations.
- Quantum Model Validation for Material Science and Chemistry: Specialized evaluation metrics have been developed for quantum mechanical models in material science and chemistry applications. These metrics assess how accurately models predict molecular properties, electronic structures, reaction energetics, and material behaviors. Validation frameworks compare computational results against experimental data and high-accuracy reference calculations to ensure reliable predictions for complex chemical systems.
- Machine Learning Integration with Quantum Model Evaluation: Machine learning techniques are increasingly used to enhance the evaluation of quantum mechanical models. These approaches include automated feature selection, error pattern recognition, and adaptive sampling strategies that optimize model performance. Hybrid evaluation frameworks combine traditional quantum mechanical metrics with machine learning-based assessments to improve model accuracy and computational efficiency.
- Quantum Information Metrics and Entanglement Measures: Evaluation metrics based on quantum information theory are essential for assessing quantum mechanical models. These include entanglement measures, quantum coherence metrics, and quantum state tomography techniques that characterize the quantum nature of the systems being modeled. Information-theoretic approaches provide insights into quantum correlations and help validate the quantum mechanical aspects of computational models.
02 Performance and Efficiency Evaluation
Quantum mechanical models are evaluated based on computational efficiency and performance metrics. These include execution time, resource utilization (qubits, gates, circuit depth), and scalability with problem size. Benchmarking frameworks compare different quantum algorithms and implementations to identify optimal approaches for specific applications. These metrics are crucial for determining the practical viability of quantum models in real-world scenarios where computational resources are limited.Expand Specific Solutions03 Fidelity and Error Rate Assessment
Fidelity metrics measure how well quantum mechanical models maintain quantum state integrity throughout computation. Error rates, including gate errors, readout errors, and decoherence effects, are quantified to assess model reliability. Quantum process tomography and randomized benchmarking techniques provide standardized methods for evaluating quantum operations. These metrics are essential for developing error mitigation strategies and improving the robustness of quantum algorithms.Expand Specific Solutions04 Validation Against Classical Benchmarks
Quantum mechanical models are often evaluated by comparing their results with established classical methods. This validation process involves benchmark problems with known solutions to verify quantum model accuracy. Metrics include quantum advantage measurements, which quantify computational speedup over classical approaches. Cross-validation techniques assess model generalizability across different datasets and problem domains, ensuring that quantum models provide reliable results across various applications.Expand Specific Solutions05 Application-Specific Evaluation Frameworks
Specialized evaluation metrics have been developed for quantum mechanical models in specific application domains. These include metrics for quantum machine learning (classification accuracy, prediction error), quantum chemistry (energy calculation precision), and quantum optimization (solution quality, convergence rate). Domain-specific benchmarking suites provide standardized test cases that enable fair comparison between different quantum approaches and help identify the most suitable models for particular use cases.Expand Specific Solutions
Leading Organizations in Quantum Computing Research
The quantum mechanical models evaluation landscape in quantum computing is currently in a transitional phase between research and early commercialization, with an estimated market size of $500-700 million that is projected to grow exponentially. Industry leaders IBM, Google, and Microsoft are advancing hardware architectures and software frameworks, while specialized players like Quantinuum (Evabode Property), Rigetti, and D-Wave are developing niche quantum solutions. Academic institutions including Harvard, University of Chicago, and Xi'an Jiaotong University are contributing fundamental research. The ecosystem shows varying technology maturity levels, with quantum simulation and cryptography applications approaching commercial viability, while fault-tolerant quantum computing remains in early research stages. Collaborative partnerships between corporations and research institutions are accelerating development across the quantum computing value chain.
International Business Machines Corp.
Technical Solution: IBM's quantum mechanical model evaluation approach centers on their Qiskit framework, which provides tools for simulating and benchmarking quantum algorithms. Their methodology includes error mitigation techniques like Zero Noise Extrapolation and Probabilistic Error Cancellation to improve the accuracy of quantum mechanical models[1]. IBM has developed the Quantum Volume metric to evaluate the performance of quantum processors, considering both the number of qubits and their quality[2]. Their latest Eagle processor with 127 qubits implements advanced 3D packaging technology to reduce crosstalk between qubits[3]. IBM's approach also includes hardware-aware compilation techniques that optimize quantum circuits based on the specific characteristics of their quantum processors, improving the fidelity of quantum mechanical simulations[4]. Their quantum error correction codes, particularly surface codes, are designed to protect quantum information against decoherence and other quantum noise sources[5].
Strengths: Comprehensive ecosystem from hardware to software; industry-leading error mitigation techniques; established quantum volume metric for standardized evaluation. Weaknesses: Quantum hardware still suffers from limited coherence times; scaling challenges with increasing qubit counts; error rates remain too high for fault-tolerant quantum computing applications.
Google LLC
Technical Solution: Google's approach to evaluating quantum mechanical models focuses on their Sycamore processor and quantum supremacy experiments. Their methodology involves comparing quantum circuit sampling tasks between quantum and classical computers to demonstrate quantum advantage[1]. Google has developed the Quantum Approximate Optimization Algorithm (QAOA) and variational quantum eigensolvers (VQE) to evaluate the performance of their quantum hardware on practical optimization problems[2]. Their error characterization techniques include cross-entropy benchmarking and randomized benchmarking to assess gate fidelities and system performance[3]. Google's Cirq framework provides tools for simulating quantum circuits and evaluating quantum mechanical models with noise models that accurately reflect their hardware characteristics[4]. Their quantum error correction research focuses on demonstrating logical qubits with improved error rates compared to physical qubits, using surface codes and other topological codes[5]. Google has also pioneered time crystals on quantum processors, demonstrating novel quantum phases of matter that can be simulated and studied on their hardware[6].
Strengths: Demonstrated quantum supremacy; advanced quantum simulation capabilities; strong focus on practical quantum advantage applications. Weaknesses: Limited qubit connectivity in their architecture; challenges in scaling beyond current processor sizes; error rates still too high for many practical applications requiring deep circuits.
Critical Patents and Breakthroughs in Quantum Models
System and method for simulating quantum mechanical models
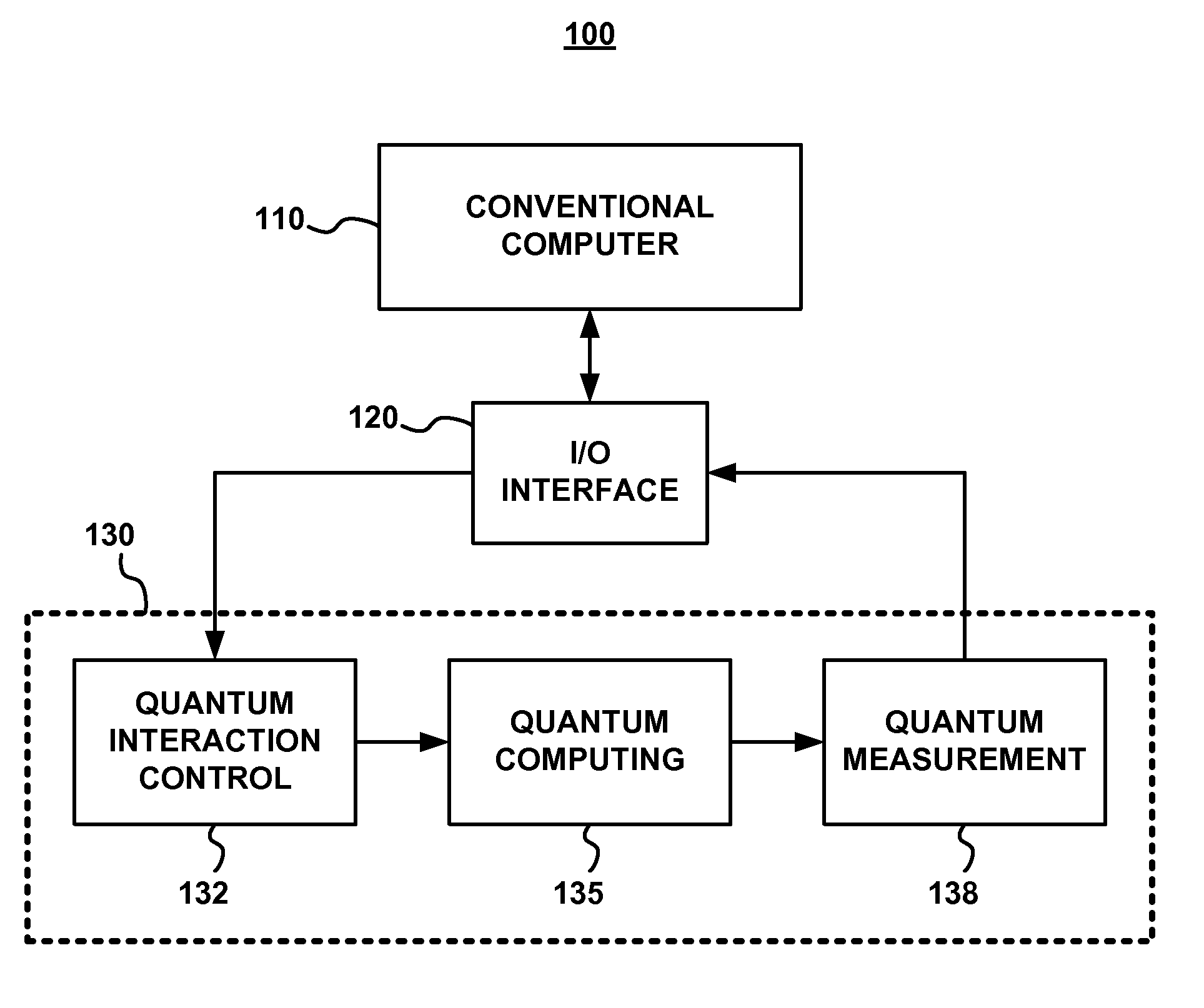
PatentPendingIN202221064464A
Innovation
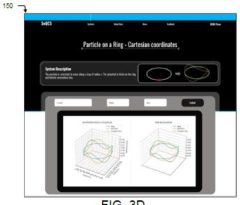
- A system that includes a processor and memory with processor-executable instructions to receive input parameters, solve equations, and generate graphical representations for quantum mechanical models such as the particle in a 1D box, 2D box, ring, harmonic oscillator, and hydrogen atom, allowing for real-time visualization and dynamic updates of boundary conditions, using scaling and descaling techniques to reduce computational requirements and accommodate a wide range of input parameters.
Estimating a quantum state of a quantum mechanical system
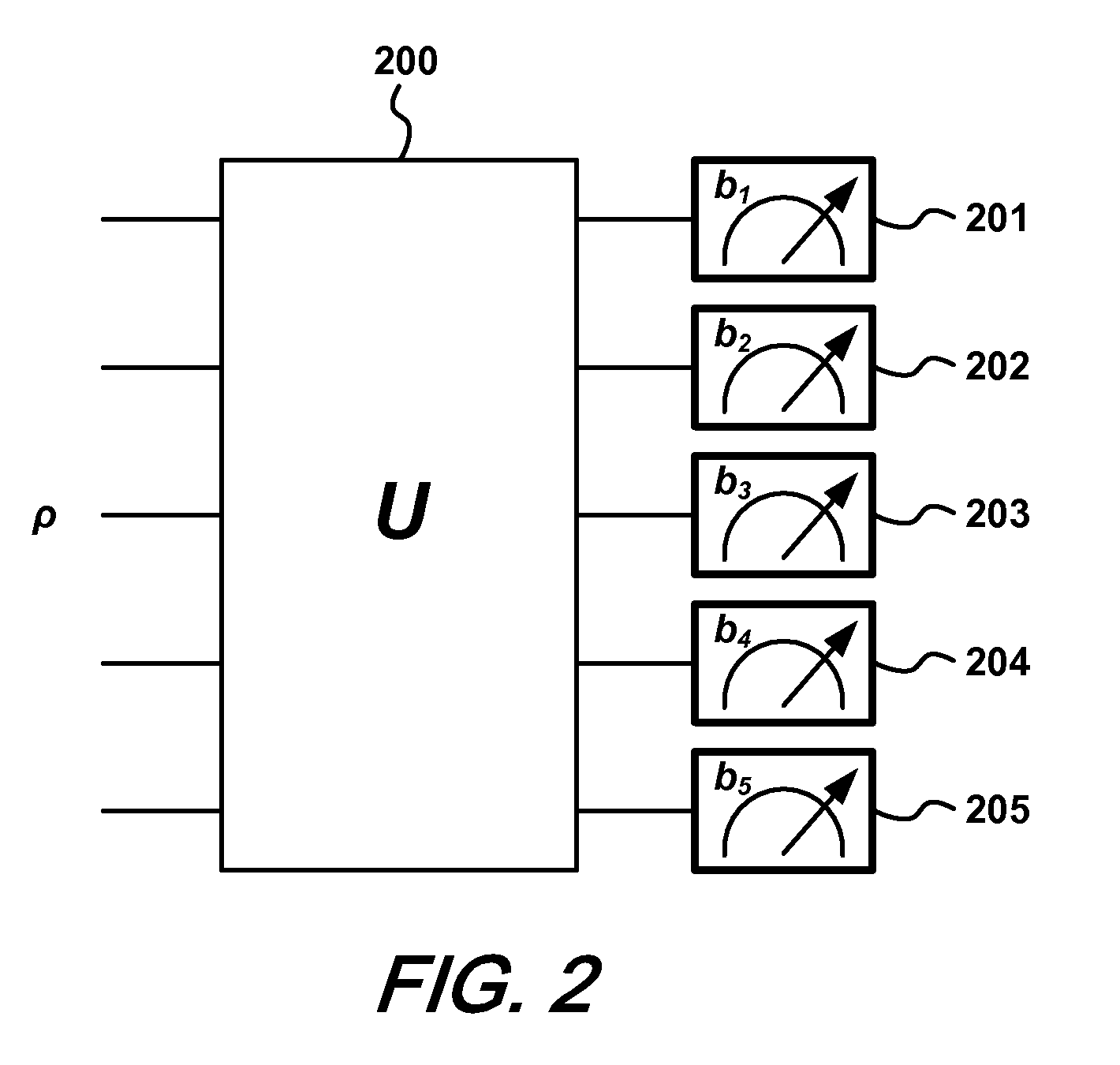
PatentInactiveUS8315969B2
Innovation
- A method using yes/no measurements of a single qubit to estimate the quantum state by applying a series of unitary operations and reconstructing the state with the expression ρ=(2d∑i=1d2-1piPi+(1-pi)(1-Pi))-(d2-2d)Id, where d is the system dimension, Pi are measurement projectors, and pi are their probabilities, allowing for efficient characterization of the quantum state with minimal measurements.
Quantum Error Correction Strategies
Quantum Error Correction (QEC) represents a critical frontier in quantum computing development, addressing the fundamental challenge of quantum decoherence and gate errors. Current quantum systems remain highly susceptible to environmental noise, with error rates typically ranging from 10^-2 to 10^-4 per gate operation—significantly higher than classical computing error rates. This vulnerability necessitates robust error correction strategies to achieve fault-tolerant quantum computation.
Surface codes have emerged as the leading QEC approach, offering practical advantages through their two-dimensional lattice structure and high error thresholds of approximately 1%. These codes encode logical qubits across multiple physical qubits in a way that allows errors to be detected and corrected without collapsing the quantum state. Recent experimental implementations by Google and IBM have demonstrated error detection capabilities, though full error correction remains challenging.
Topological quantum codes represent another promising direction, with Kitaev's toric code and color codes showing theoretical resilience against local errors. These approaches leverage topological properties to protect quantum information, potentially requiring fewer physical resources than traditional QEC methods. Microsoft's topological quantum computing initiative focuses on this approach, though experimental realization remains in early stages.
Quantum Low-Density Parity-Check (qLDPC) codes have recently gained attention for their potential to achieve good error correction with more favorable overhead requirements. These codes adapt classical LDPC principles to the quantum domain, with theoretical work suggesting they may approach the quantum Singleton bound more efficiently than surface codes.
Hardware-specific QEC strategies are also emerging, tailored to particular quantum computing architectures. For superconducting qubits, cat codes and bosonic codes exploit higher-dimensional Hilbert spaces to encode quantum information redundantly. In trapped-ion systems, sympathetic cooling techniques combined with error detection protocols have demonstrated promising results in maintaining qubit coherence.
Quantum error mitigation techniques complement formal QEC by reducing errors without full error correction overhead. Zero-noise extrapolation, probabilistic error cancellation, and dynamical decoupling protocols have shown practical utility in current NISQ (Noisy Intermediate-Scale Quantum) devices, extending coherence times and improving computational accuracy without the substantial qubit overhead required by full QEC implementations.
The resource requirements for implementing effective QEC remain substantial, with estimates suggesting that thousands of physical qubits may be needed per logical qubit to achieve fault tolerance. This overhead presents a significant scaling challenge that quantum hardware must overcome to realize practical quantum advantage in complex computational tasks.
Surface codes have emerged as the leading QEC approach, offering practical advantages through their two-dimensional lattice structure and high error thresholds of approximately 1%. These codes encode logical qubits across multiple physical qubits in a way that allows errors to be detected and corrected without collapsing the quantum state. Recent experimental implementations by Google and IBM have demonstrated error detection capabilities, though full error correction remains challenging.
Topological quantum codes represent another promising direction, with Kitaev's toric code and color codes showing theoretical resilience against local errors. These approaches leverage topological properties to protect quantum information, potentially requiring fewer physical resources than traditional QEC methods. Microsoft's topological quantum computing initiative focuses on this approach, though experimental realization remains in early stages.
Quantum Low-Density Parity-Check (qLDPC) codes have recently gained attention for their potential to achieve good error correction with more favorable overhead requirements. These codes adapt classical LDPC principles to the quantum domain, with theoretical work suggesting they may approach the quantum Singleton bound more efficiently than surface codes.
Hardware-specific QEC strategies are also emerging, tailored to particular quantum computing architectures. For superconducting qubits, cat codes and bosonic codes exploit higher-dimensional Hilbert spaces to encode quantum information redundantly. In trapped-ion systems, sympathetic cooling techniques combined with error detection protocols have demonstrated promising results in maintaining qubit coherence.
Quantum error mitigation techniques complement formal QEC by reducing errors without full error correction overhead. Zero-noise extrapolation, probabilistic error cancellation, and dynamical decoupling protocols have shown practical utility in current NISQ (Noisy Intermediate-Scale Quantum) devices, extending coherence times and improving computational accuracy without the substantial qubit overhead required by full QEC implementations.
The resource requirements for implementing effective QEC remain substantial, with estimates suggesting that thousands of physical qubits may be needed per logical qubit to achieve fault tolerance. This overhead presents a significant scaling challenge that quantum hardware must overcome to realize practical quantum advantage in complex computational tasks.
Quantum Computing Benchmarking Methodologies
Quantum Computing Benchmarking Methodologies have become increasingly critical as quantum technologies transition from theoretical constructs to practical implementations. The establishment of standardized evaluation frameworks enables objective comparison between different quantum computing platforms and algorithms. Current methodologies typically focus on three key dimensions: computational accuracy, execution time, and resource efficiency. These metrics provide a comprehensive assessment of quantum mechanical models when applied to specific computing tasks.
The quantum volume metric, introduced by IBM, represents one of the most widely adopted benchmarking approaches. This single-number metric quantifies the largest random circuit of equal width and depth that a quantum computer can successfully implement. Complementary to this, Quantum Approximate Optimization Algorithm (QAOA) benchmarks evaluate how effectively quantum systems can solve combinatorial optimization problems, while Variational Quantum Eigensolver (VQE) benchmarks assess performance on quantum chemistry simulations.
Cross-platform benchmarking initiatives have emerged to address the heterogeneity of quantum computing architectures. The Quantum Economic Development Consortium (QED-C) has developed technology-agnostic test suites that enable fair comparisons between superconducting, trapped-ion, photonic, and other quantum computing implementations. These standardized tests measure gate fidelity, coherence times, and algorithm-specific performance metrics across different hardware platforms.
Error mitigation benchmarks have gained prominence as researchers recognize that near-term quantum devices will operate without full error correction. These methodologies evaluate how effectively different quantum mechanical models can compensate for noise and decoherence effects. Techniques such as zero-noise extrapolation and probabilistic error cancellation are quantitatively assessed based on their ability to improve computational outcomes on noisy intermediate-scale quantum (NISQ) devices.
Application-specific benchmarks provide context-relevant evaluation frameworks for quantum mechanical models. For machine learning tasks, metrics focus on classification accuracy and training convergence rates. For cryptographic applications, benchmarks evaluate the efficiency of period-finding and integer factorization. Financial modeling applications are assessed based on portfolio optimization accuracy and option pricing precision.
The quantum computing community continues to refine these methodologies through collaborative initiatives like the IEEE Quantum Computing Performance Metrics Working Group. Their efforts aim to establish industry-wide standards that facilitate transparent reporting of quantum system capabilities and limitations, ultimately accelerating progress toward quantum advantage in practical computing tasks.
The quantum volume metric, introduced by IBM, represents one of the most widely adopted benchmarking approaches. This single-number metric quantifies the largest random circuit of equal width and depth that a quantum computer can successfully implement. Complementary to this, Quantum Approximate Optimization Algorithm (QAOA) benchmarks evaluate how effectively quantum systems can solve combinatorial optimization problems, while Variational Quantum Eigensolver (VQE) benchmarks assess performance on quantum chemistry simulations.
Cross-platform benchmarking initiatives have emerged to address the heterogeneity of quantum computing architectures. The Quantum Economic Development Consortium (QED-C) has developed technology-agnostic test suites that enable fair comparisons between superconducting, trapped-ion, photonic, and other quantum computing implementations. These standardized tests measure gate fidelity, coherence times, and algorithm-specific performance metrics across different hardware platforms.
Error mitigation benchmarks have gained prominence as researchers recognize that near-term quantum devices will operate without full error correction. These methodologies evaluate how effectively different quantum mechanical models can compensate for noise and decoherence effects. Techniques such as zero-noise extrapolation and probabilistic error cancellation are quantitatively assessed based on their ability to improve computational outcomes on noisy intermediate-scale quantum (NISQ) devices.
Application-specific benchmarks provide context-relevant evaluation frameworks for quantum mechanical models. For machine learning tasks, metrics focus on classification accuracy and training convergence rates. For cryptographic applications, benchmarks evaluate the efficiency of period-finding and integer factorization. Financial modeling applications are assessed based on portfolio optimization accuracy and option pricing precision.
The quantum computing community continues to refine these methodologies through collaborative initiatives like the IEEE Quantum Computing Performance Metrics Working Group. Their efforts aim to establish industry-wide standards that facilitate transparent reporting of quantum system capabilities and limitations, ultimately accelerating progress toward quantum advantage in practical computing tasks.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!