How to Refine Quantum Model Algorithms for Precision
SEP 4, 202510 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Quantum Algorithm Refinement Background and Objectives
Quantum computing has evolved significantly since its theoretical inception in the early 1980s, progressing from abstract mathematical concepts to increasingly practical implementations. The refinement of quantum algorithms for precision represents a critical frontier in this evolution, addressing the fundamental challenge of extracting reliable results from inherently probabilistic quantum systems. This technical domain has gained momentum particularly over the past decade, as quantum hardware capabilities have advanced beyond proof-of-concept demonstrations toward practical quantum advantage.
The historical trajectory of quantum algorithm development reveals a pattern of theoretical innovation followed by implementation challenges. Early quantum algorithms such as Shor's and Grover's demonstrated theoretical superiority over classical counterparts but remained largely academic exercises due to hardware limitations. Recent years have witnessed a shift toward hybrid quantum-classical approaches and error mitigation techniques, representing pragmatic adaptations to current technological constraints.
Current precision challenges in quantum algorithms stem from multiple sources: quantum decoherence, gate errors, measurement uncertainties, and the probabilistic nature of quantum mechanics itself. These factors collectively contribute to what researchers term the "quantum noise barrier" - a fundamental limitation that must be overcome to achieve reliable quantum computation at scale.
The technical objectives for quantum algorithm refinement center on several interconnected goals. Primary among these is the development of robust error correction and mitigation techniques that can function effectively on near-term quantum devices with limited qubit counts and coherence times. Equally important is the optimization of algorithm design to minimize circuit depth and gate requirements, thereby reducing opportunities for error accumulation.
Another critical objective involves improving the precision of quantum state preparation and measurement processes, as these represent the input and output interfaces between classical and quantum computational domains. Advances in these areas directly impact the overall reliability of quantum computational results.
The field is also pursuing algorithmic innovations that can extract maximum utility from noisy intermediate-scale quantum (NISQ) devices while simultaneously developing scalable approaches that will remain viable as quantum hardware capabilities expand. This dual-track approach acknowledges both near-term practical constraints and long-term aspirations for fault-tolerant quantum computing.
Industry expectations for quantum algorithm precision have evolved from theoretical interest to practical benchmarks, with increasing emphasis on demonstrating quantum advantage in real-world applications. This shift reflects growing investment in quantum technologies and heightened anticipation of commercial applications across sectors including cryptography, materials science, pharmaceutical development, and financial modeling.
The historical trajectory of quantum algorithm development reveals a pattern of theoretical innovation followed by implementation challenges. Early quantum algorithms such as Shor's and Grover's demonstrated theoretical superiority over classical counterparts but remained largely academic exercises due to hardware limitations. Recent years have witnessed a shift toward hybrid quantum-classical approaches and error mitigation techniques, representing pragmatic adaptations to current technological constraints.
Current precision challenges in quantum algorithms stem from multiple sources: quantum decoherence, gate errors, measurement uncertainties, and the probabilistic nature of quantum mechanics itself. These factors collectively contribute to what researchers term the "quantum noise barrier" - a fundamental limitation that must be overcome to achieve reliable quantum computation at scale.
The technical objectives for quantum algorithm refinement center on several interconnected goals. Primary among these is the development of robust error correction and mitigation techniques that can function effectively on near-term quantum devices with limited qubit counts and coherence times. Equally important is the optimization of algorithm design to minimize circuit depth and gate requirements, thereby reducing opportunities for error accumulation.
Another critical objective involves improving the precision of quantum state preparation and measurement processes, as these represent the input and output interfaces between classical and quantum computational domains. Advances in these areas directly impact the overall reliability of quantum computational results.
The field is also pursuing algorithmic innovations that can extract maximum utility from noisy intermediate-scale quantum (NISQ) devices while simultaneously developing scalable approaches that will remain viable as quantum hardware capabilities expand. This dual-track approach acknowledges both near-term practical constraints and long-term aspirations for fault-tolerant quantum computing.
Industry expectations for quantum algorithm precision have evolved from theoretical interest to practical benchmarks, with increasing emphasis on demonstrating quantum advantage in real-world applications. This shift reflects growing investment in quantum technologies and heightened anticipation of commercial applications across sectors including cryptography, materials science, pharmaceutical development, and financial modeling.
Market Applications for High-Precision Quantum Models
High-precision quantum models are poised to revolutionize multiple industries by offering unprecedented computational capabilities for complex problems. The financial sector stands as a primary beneficiary, with quantum algorithms enabling more accurate risk assessment models, portfolio optimization strategies, and fraud detection systems. Major financial institutions including JPMorgan Chase and Goldman Sachs have already established quantum computing research divisions to leverage these advantages in high-frequency trading and complex derivatives pricing.
In healthcare and pharmaceutical development, refined quantum models demonstrate exceptional promise for drug discovery and molecular simulation. These models can analyze molecular interactions with greater precision than classical computing approaches, potentially reducing drug development timelines from years to months. Companies like Roche and Pfizer are exploring quantum-enhanced algorithms for protein folding simulations and personalized medicine applications, where precision is paramount for treatment efficacy.
The manufacturing sector is embracing quantum precision for materials science applications, with automotive and aerospace industries leading adoption. Boeing and Airbus are investigating quantum algorithms for optimizing composite material designs and structural integrity simulations. These applications require extreme computational precision to model atomic-level interactions that determine macroscopic material properties.
Climate modeling represents another critical application area where precision quantum algorithms offer transformative potential. Current climate models suffer from significant uncertainty margins, but quantum-enhanced simulations could provide more accurate predictions of climate patterns, extreme weather events, and environmental changes. Government agencies and research institutions across Europe, North America, and Asia are investing in quantum climate modeling capabilities.
Logistics and supply chain optimization benefit substantially from high-precision quantum models through more efficient route planning, inventory management, and demand forecasting. Companies like Amazon and DHL are exploring quantum algorithms to solve complex optimization problems that classical computers struggle to address efficiently, potentially reducing operational costs while improving service reliability.
The cybersecurity sector represents perhaps the most urgent application area, as quantum computing threatens existing encryption standards while simultaneously offering new quantum-resistant security protocols. Financial institutions, government agencies, and technology companies are investing heavily in quantum-secure communications and cryptographic systems that rely on precisely calibrated quantum algorithms.
Market analysis indicates that early commercial applications of high-precision quantum models will focus on hybrid classical-quantum systems that address specific computational bottlenecks in existing workflows rather than complete system replacements. This approach allows organizations to incrementally adopt quantum advantages while managing implementation risks and infrastructure costs.
In healthcare and pharmaceutical development, refined quantum models demonstrate exceptional promise for drug discovery and molecular simulation. These models can analyze molecular interactions with greater precision than classical computing approaches, potentially reducing drug development timelines from years to months. Companies like Roche and Pfizer are exploring quantum-enhanced algorithms for protein folding simulations and personalized medicine applications, where precision is paramount for treatment efficacy.
The manufacturing sector is embracing quantum precision for materials science applications, with automotive and aerospace industries leading adoption. Boeing and Airbus are investigating quantum algorithms for optimizing composite material designs and structural integrity simulations. These applications require extreme computational precision to model atomic-level interactions that determine macroscopic material properties.
Climate modeling represents another critical application area where precision quantum algorithms offer transformative potential. Current climate models suffer from significant uncertainty margins, but quantum-enhanced simulations could provide more accurate predictions of climate patterns, extreme weather events, and environmental changes. Government agencies and research institutions across Europe, North America, and Asia are investing in quantum climate modeling capabilities.
Logistics and supply chain optimization benefit substantially from high-precision quantum models through more efficient route planning, inventory management, and demand forecasting. Companies like Amazon and DHL are exploring quantum algorithms to solve complex optimization problems that classical computers struggle to address efficiently, potentially reducing operational costs while improving service reliability.
The cybersecurity sector represents perhaps the most urgent application area, as quantum computing threatens existing encryption standards while simultaneously offering new quantum-resistant security protocols. Financial institutions, government agencies, and technology companies are investing heavily in quantum-secure communications and cryptographic systems that rely on precisely calibrated quantum algorithms.
Market analysis indicates that early commercial applications of high-precision quantum models will focus on hybrid classical-quantum systems that address specific computational bottlenecks in existing workflows rather than complete system replacements. This approach allows organizations to incrementally adopt quantum advantages while managing implementation risks and infrastructure costs.
Current Quantum Algorithm Limitations and Challenges
Despite significant advancements in quantum computing, current quantum algorithms face substantial limitations that impede their precision and practical implementation. Quantum decoherence remains one of the most formidable challenges, as quantum systems are extremely sensitive to environmental interactions. These interactions cause quantum states to lose their coherence rapidly, resulting in computational errors that compound throughout algorithm execution. Even with error correction techniques, maintaining quantum coherence for sufficiently long periods to complete complex calculations remains problematic.
Quantum noise presents another critical limitation, manifesting as random fluctuations that distort quantum signals and reduce computational accuracy. This noise arises from various sources including thermal vibrations, electromagnetic interference, and imperfections in quantum hardware. The signal-to-noise ratio in quantum systems deteriorates as the number of qubits increases, creating a significant scaling challenge for precision-oriented applications.
Gate fidelity issues further complicate quantum algorithm precision. Current quantum gates operate with error rates typically ranging from 0.1% to several percent per operation. While this may seem minimal, complex algorithms requiring thousands or millions of gate operations experience compounded errors that render results unreliable. The threshold theorem suggests that quantum error correction becomes effective only when gate error rates fall below certain thresholds, which many current implementations have yet to achieve.
The limited qubit connectivity in physical quantum processors constrains algorithm design and execution. Most quantum hardware architectures do not allow arbitrary qubit-to-qubit interactions, necessitating additional SWAP operations that increase circuit depth and error accumulation. This topology constraint significantly impacts algorithm precision, especially for problems requiring extensive qubit entanglement across the system.
Measurement errors represent another substantial challenge, as the process of extracting information from quantum systems is inherently probabilistic and prone to inaccuracies. Current measurement techniques often disturb quantum states in ways that introduce additional uncertainties into the final results.
Algorithm-specific limitations also exist. Quantum phase estimation, crucial for many quantum algorithms, requires extremely precise phase rotations that current hardware struggles to implement accurately. Similarly, quantum amplitude estimation techniques face precision barriers due to the finite sampling nature of quantum measurements.
The absence of standardized benchmarking methodologies further complicates progress assessment. Without consistent metrics for quantum algorithm precision across different hardware platforms and problem domains, comparing solutions and identifying optimal approaches becomes challenging. This lack of standardization hinders systematic improvement efforts in quantum algorithm refinement.
Quantum noise presents another critical limitation, manifesting as random fluctuations that distort quantum signals and reduce computational accuracy. This noise arises from various sources including thermal vibrations, electromagnetic interference, and imperfections in quantum hardware. The signal-to-noise ratio in quantum systems deteriorates as the number of qubits increases, creating a significant scaling challenge for precision-oriented applications.
Gate fidelity issues further complicate quantum algorithm precision. Current quantum gates operate with error rates typically ranging from 0.1% to several percent per operation. While this may seem minimal, complex algorithms requiring thousands or millions of gate operations experience compounded errors that render results unreliable. The threshold theorem suggests that quantum error correction becomes effective only when gate error rates fall below certain thresholds, which many current implementations have yet to achieve.
The limited qubit connectivity in physical quantum processors constrains algorithm design and execution. Most quantum hardware architectures do not allow arbitrary qubit-to-qubit interactions, necessitating additional SWAP operations that increase circuit depth and error accumulation. This topology constraint significantly impacts algorithm precision, especially for problems requiring extensive qubit entanglement across the system.
Measurement errors represent another substantial challenge, as the process of extracting information from quantum systems is inherently probabilistic and prone to inaccuracies. Current measurement techniques often disturb quantum states in ways that introduce additional uncertainties into the final results.
Algorithm-specific limitations also exist. Quantum phase estimation, crucial for many quantum algorithms, requires extremely precise phase rotations that current hardware struggles to implement accurately. Similarly, quantum amplitude estimation techniques face precision barriers due to the finite sampling nature of quantum measurements.
The absence of standardized benchmarking methodologies further complicates progress assessment. Without consistent metrics for quantum algorithm precision across different hardware platforms and problem domains, comparing solutions and identifying optimal approaches becomes challenging. This lack of standardization hinders systematic improvement efforts in quantum algorithm refinement.
Existing Precision Enhancement Techniques for Quantum Models
01 Quantum algorithms for enhanced computational precision
Quantum algorithms can significantly improve computational precision compared to classical methods. These algorithms leverage quantum superposition and entanglement to perform complex calculations with higher accuracy. By utilizing quantum properties, these algorithms can achieve exponential speedups for certain problems while maintaining or improving precision levels, particularly in simulations of physical systems and optimization problems.- Quantum algorithm optimization for enhanced precision: Quantum algorithms can be optimized to achieve higher precision in computational models. These optimizations involve refining quantum circuits, reducing noise interference, and implementing error correction techniques. By enhancing the precision of quantum algorithms, more accurate results can be obtained for complex computational problems, particularly in fields requiring high numerical accuracy.
- Quantum machine learning models for improved prediction accuracy: Quantum machine learning models leverage quantum computing principles to improve prediction accuracy beyond classical approaches. These models utilize quantum superposition and entanglement to process complex datasets more efficiently. By implementing quantum neural networks and quantum support vector machines, these systems can achieve higher precision in pattern recognition, classification tasks, and predictive analytics.
- Error mitigation techniques in quantum computational models: Various error mitigation techniques have been developed to enhance the precision of quantum computational models. These include noise-aware algorithm design, dynamical decoupling protocols, and zero-noise extrapolation methods. By systematically identifying and compensating for quantum noise sources, these techniques significantly improve the reliability and accuracy of quantum calculations, enabling more precise modeling of complex systems.
- Hybrid quantum-classical algorithms for precision enhancement: Hybrid quantum-classical algorithms combine the strengths of both computing paradigms to achieve higher precision in computational models. These approaches delegate specific precision-critical tasks to quantum processors while using classical computers for other operations. The synergistic integration allows for optimized resource allocation, noise reduction, and enhanced computational accuracy, particularly for applications in chemistry, materials science, and financial modeling.
- Quantum simulation frameworks for high-precision modeling: Specialized quantum simulation frameworks have been developed to enable high-precision modeling of complex physical systems. These frameworks utilize quantum algorithms specifically designed to simulate quantum mechanical phenomena with unprecedented accuracy. By leveraging quantum resources to model quantum systems, these approaches avoid the exponential complexity faced by classical computers, allowing for more precise simulations of molecular interactions, material properties, and quantum field theories.
02 Error mitigation techniques in quantum models
Various error mitigation techniques have been developed to improve the precision of quantum models. These include error correction codes, noise-resilient algorithm design, and hybrid quantum-classical approaches. By implementing these techniques, quantum computations can achieve higher fidelity results even on noisy intermediate-scale quantum (NISQ) devices, leading to more reliable and precise outcomes for complex computational tasks.Expand Specific Solutions03 Quantum machine learning models for precision enhancement
Quantum machine learning models combine quantum computing principles with machine learning techniques to enhance precision in data analysis and prediction tasks. These models utilize quantum circuits to process information in ways that classical computers cannot, enabling more accurate pattern recognition and classification. The quantum advantage in dimensionality and feature space exploration allows for improved precision in various applications including financial modeling, drug discovery, and materials science.Expand Specific Solutions04 Variational quantum algorithms for optimization precision
Variational quantum algorithms provide a framework for solving optimization problems with high precision. These hybrid quantum-classical algorithms use parameterized quantum circuits that are iteratively optimized to find solutions to complex problems. By adjusting the circuit parameters based on measurement outcomes, these algorithms can achieve precise results for optimization tasks in chemistry, finance, and logistics, even with limited quantum resources.Expand Specific Solutions05 Quantum simulation models for high-precision scientific applications
Quantum simulation models enable high-precision scientific applications by directly leveraging quantum systems to simulate other quantum systems. These models can accurately represent quantum mechanical phenomena that are computationally intractable for classical computers. The inherent quantum nature of these simulations allows for unprecedented precision in modeling molecular interactions, material properties, and chemical reactions, potentially revolutionizing fields such as drug development, materials science, and catalysis research.Expand Specific Solutions
Leading Organizations in Quantum Algorithm Development
Quantum model algorithm refinement is currently in an early growth phase, with the market expanding rapidly as quantum computing transitions from research to practical applications. The global market size for quantum computing is projected to reach significant scale by 2030, though precision refinement technologies remain in developmental stages. In terms of technical maturity, industry leaders like IBM, Google, and Fujitsu are making substantial advances in error correction and algorithm optimization, while specialized players such as Origin Quantum and Blaize focus on niche refinement approaches. Academic institutions including Beihang University and UCL collaborate with industry partners like Samsung and Huawei to bridge theoretical advances with practical implementations. The competitive landscape features both established technology corporations and quantum-focused startups working to overcome precision limitations in current quantum models.
Google LLC
Technical Solution: Google's approach to quantum algorithm precision refinement is built around their Quantum AI platform and Cirq framework. Their strategy employs dynamic decoupling sequences that shield qubits from environmental noise by applying precisely timed control pulses. Google has pioneered the use of quantum supremacy experiments to benchmark and improve algorithm precision, demonstrating a 53-qubit processor performing tasks exponentially faster than classical supercomputers. Their error mitigation techniques include Floquet calibration, which characterizes and compensates for coherent errors in quantum gates. Google has developed variational algorithms like QAOA (Quantum Approximate Optimization Algorithm) that are inherently more robust to certain types of noise. Their recent work on Sycamore and subsequent processors implements mid-circuit measurements with conditional operations, allowing for error detection and correction during algorithm execution. Google's quantum error correction research focuses on surface codes that can detect and correct errors with minimal overhead, achieving error rates below threshold levels required for fault-tolerant quantum computing.
Strengths: Advanced hardware architecture optimized for high-fidelity operations; strong focus on practical quantum advantage demonstrations; robust software tools for algorithm development and testing. Weaknesses: Their approach sometimes prioritizes quantum volume over error correction capabilities; some techniques require significant classical computing resources to process and correct quantum results.
International Business Machines Corp.
Technical Solution: IBM's approach to refining quantum model algorithms for precision centers on their Qiskit framework and error mitigation techniques. Their Quantum Error Correction (QEC) protocols implement logical qubits that are more resilient to noise than physical qubits. IBM has developed Zero-Noise Extrapolation (ZNE) which runs algorithms at different noise levels and extrapolates to zero-noise results, significantly improving precision. Their Probabilistic Error Cancellation (PEC) technique characterizes noise in quantum gates and inverts it mathematically. IBM's quantum volume metric helps quantify the effective computational power of quantum systems, allowing for targeted improvements. Recently, they've introduced dynamic circuits that adapt during execution based on intermediate measurements, reducing cumulative errors in complex algorithms. Their latest Eagle processor with 127 qubits implements advanced error suppression techniques that have shown up to 5x improvement in algorithm precision compared to previous generations.
Strengths: Comprehensive error mitigation toolkit that addresses multiple sources of quantum noise; industry-leading hardware with increasing qubit counts and coherence times; extensive software ecosystem supporting algorithm development. Weaknesses: Many error correction techniques require significant overhead in terms of additional qubits; some approaches are computationally intensive and may limit practical applications in near-term devices.
Key Innovations in Quantum Error Correction Methods
Amplitude estimation method
PatentPendingUS20250028988A1
Innovation
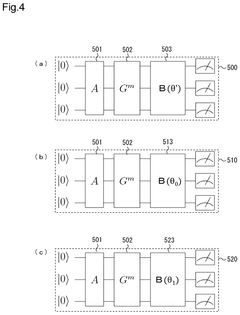
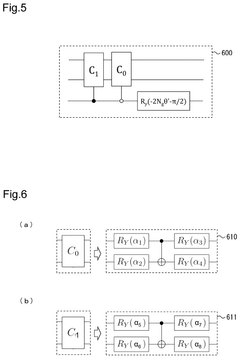
- The proposed method involves a three-stage computation process: pre-computation to adjust the parameter α of the variational quantum circuit, a preceding computation to obtain a rough estimated value of the parameter θ, and a subsequent computation to adjust the measurement basis using the estimated values of θ and α, thereby improving the estimation accuracy.
Optimizing development of a quantum circuit or a quantum model
PatentPendingUS20250131300A1
Innovation
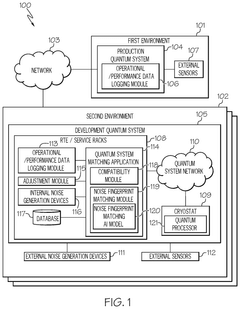
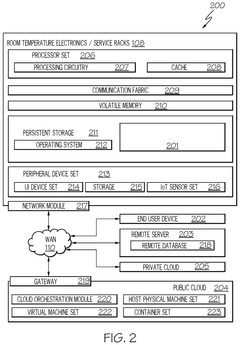
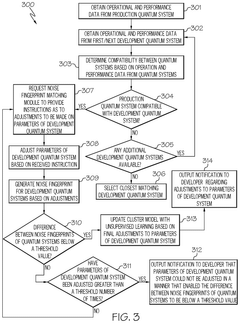
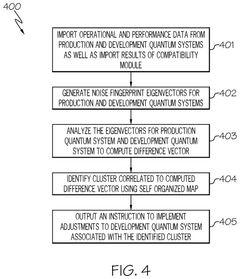
- The method involves obtaining operational and performance data from both development and production quantum systems, generating noise fingerprints for each, and adjusting the parameters of the development system until the difference between the two noise fingerprints is below a threshold value, thereby matching the noise environment of the production system.
Quantum Hardware-Algorithm Co-design Approaches
Quantum Hardware-Algorithm Co-design Approaches represents a paradigm shift in quantum computing development, where hardware capabilities and algorithmic design are considered simultaneously rather than in isolation. This integrated approach acknowledges the intrinsic relationship between quantum algorithms and the physical systems that execute them, enabling more precise and efficient quantum models.
The co-design methodology begins with understanding the specific constraints and capabilities of available quantum hardware platforms. Different quantum technologies—superconducting qubits, trapped ions, photonic systems, and topological qubits—each present unique characteristics regarding coherence times, gate fidelities, connectivity, and noise profiles. By tailoring algorithms to leverage the strengths and mitigate the weaknesses of specific hardware implementations, researchers can achieve significant improvements in computational precision.
Error mitigation techniques form a crucial component of hardware-algorithm co-design. Rather than developing generic algorithms and subsequently adapting them to hardware limitations, co-design incorporates error awareness from the outset. This includes noise-aware circuit compilation, where quantum operations are optimized based on the error characteristics of specific hardware components, and dynamic circuit restructuring that adapts to real-time measurements of hardware performance.
Variational algorithms exemplify successful hardware-algorithm co-design approaches. These hybrid quantum-classical methods, including Variational Quantum Eigensolvers (VQE) and Quantum Approximate Optimization Algorithms (QAOA), are inherently adaptable to hardware constraints. Their parameterized nature allows for optimization that accounts for device-specific noise patterns and connectivity limitations, effectively turning hardware constraints into features of the optimization landscape.
Recent advances in pulse-level control have further enhanced co-design capabilities. By moving beyond abstract gate-level programming to direct manipulation of the underlying control pulses, algorithms can be fine-tuned to maximize fidelity on specific hardware. This approach has demonstrated improvements in precision by reducing gate errors and optimizing implementation efficiency.
Industry-academia partnerships have accelerated progress in hardware-algorithm co-design. Companies like IBM, Google, and Rigetti collaborate with research institutions to develop algorithms specifically optimized for their respective quantum processors. These collaborations have yielded specialized compiler tools that translate abstract quantum algorithms into hardware-efficient implementations, considering factors such as qubit topology, native gate sets, and calibration data.
The future of quantum hardware-algorithm co-design lies in automated optimization frameworks that can dynamically adapt quantum algorithms to evolving hardware capabilities. Machine learning approaches are increasingly being employed to predict hardware behavior and automatically generate optimized circuit implementations, promising further refinements in quantum model precision without requiring manual intervention for each hardware iteration.
The co-design methodology begins with understanding the specific constraints and capabilities of available quantum hardware platforms. Different quantum technologies—superconducting qubits, trapped ions, photonic systems, and topological qubits—each present unique characteristics regarding coherence times, gate fidelities, connectivity, and noise profiles. By tailoring algorithms to leverage the strengths and mitigate the weaknesses of specific hardware implementations, researchers can achieve significant improvements in computational precision.
Error mitigation techniques form a crucial component of hardware-algorithm co-design. Rather than developing generic algorithms and subsequently adapting them to hardware limitations, co-design incorporates error awareness from the outset. This includes noise-aware circuit compilation, where quantum operations are optimized based on the error characteristics of specific hardware components, and dynamic circuit restructuring that adapts to real-time measurements of hardware performance.
Variational algorithms exemplify successful hardware-algorithm co-design approaches. These hybrid quantum-classical methods, including Variational Quantum Eigensolvers (VQE) and Quantum Approximate Optimization Algorithms (QAOA), are inherently adaptable to hardware constraints. Their parameterized nature allows for optimization that accounts for device-specific noise patterns and connectivity limitations, effectively turning hardware constraints into features of the optimization landscape.
Recent advances in pulse-level control have further enhanced co-design capabilities. By moving beyond abstract gate-level programming to direct manipulation of the underlying control pulses, algorithms can be fine-tuned to maximize fidelity on specific hardware. This approach has demonstrated improvements in precision by reducing gate errors and optimizing implementation efficiency.
Industry-academia partnerships have accelerated progress in hardware-algorithm co-design. Companies like IBM, Google, and Rigetti collaborate with research institutions to develop algorithms specifically optimized for their respective quantum processors. These collaborations have yielded specialized compiler tools that translate abstract quantum algorithms into hardware-efficient implementations, considering factors such as qubit topology, native gate sets, and calibration data.
The future of quantum hardware-algorithm co-design lies in automated optimization frameworks that can dynamically adapt quantum algorithms to evolving hardware capabilities. Machine learning approaches are increasingly being employed to predict hardware behavior and automatically generate optimized circuit implementations, promising further refinements in quantum model precision without requiring manual intervention for each hardware iteration.
Standardization Efforts in Quantum Algorithm Benchmarking
The quantum computing field has recognized the critical need for standardized benchmarking frameworks to evaluate and compare quantum algorithms effectively. Several international organizations have initiated collaborative efforts to establish common metrics, methodologies, and reporting standards for quantum algorithm performance. The IEEE Quantum Computing Working Group has developed the IEEE P7131 standard specifically addressing quantum algorithm benchmarking, providing guidelines for consistent performance evaluation across different quantum computing platforms.
The Quantum Economic Development Consortium (QED-C) has established a Technical Advisory Committee focused on performance metrics and benchmarks, bringing together industry leaders, academic researchers, and government representatives to create consensus-based standards for quantum algorithm precision assessment. Their framework includes standardized test suites designed to evaluate algorithmic accuracy under various noise conditions.
The International Organization for Standardization (ISO) has formed the ISO/IEC JTC 1/SC 42 committee, which is developing standards for quantum computing that include benchmarking protocols for algorithm precision. Their work emphasizes reproducibility and transparency in reporting quantum algorithm performance results.
Academic institutions have also contributed significantly to standardization efforts. The Quantum Algorithm Zoo, maintained by the National Institute of Standards and Technology (NIST), catalogs quantum algorithms and is working to incorporate standardized precision metrics. This resource serves as a reference point for researchers seeking to compare algorithm performance across different implementations.
Industry consortia like the Quantum Industry Consortium (QuIC) in Europe have established working groups dedicated to benchmarking standards, focusing on application-specific metrics that evaluate precision in real-world use cases rather than abstract theoretical measures. Their approach emphasizes practical utility in fields such as chemistry simulation, optimization, and machine learning.
Open-source initiatives have emerged as crucial enablers of standardization. Projects like Quantum Open Source Foundation (QOSF) and Quantum Benchmark Suite provide community-developed benchmarking tools that implement emerging standards, allowing researchers to evaluate their algorithms against established baselines. These tools typically include precision metrics such as quantum volume, circuit layer operations per second (CLOPS), and application-specific error rates.
The convergence of these standardization efforts is gradually creating a common language for discussing and evaluating quantum algorithm precision, enabling more meaningful comparisons between different approaches and accelerating progress toward practical quantum advantage.
The Quantum Economic Development Consortium (QED-C) has established a Technical Advisory Committee focused on performance metrics and benchmarks, bringing together industry leaders, academic researchers, and government representatives to create consensus-based standards for quantum algorithm precision assessment. Their framework includes standardized test suites designed to evaluate algorithmic accuracy under various noise conditions.
The International Organization for Standardization (ISO) has formed the ISO/IEC JTC 1/SC 42 committee, which is developing standards for quantum computing that include benchmarking protocols for algorithm precision. Their work emphasizes reproducibility and transparency in reporting quantum algorithm performance results.
Academic institutions have also contributed significantly to standardization efforts. The Quantum Algorithm Zoo, maintained by the National Institute of Standards and Technology (NIST), catalogs quantum algorithms and is working to incorporate standardized precision metrics. This resource serves as a reference point for researchers seeking to compare algorithm performance across different implementations.
Industry consortia like the Quantum Industry Consortium (QuIC) in Europe have established working groups dedicated to benchmarking standards, focusing on application-specific metrics that evaluate precision in real-world use cases rather than abstract theoretical measures. Their approach emphasizes practical utility in fields such as chemistry simulation, optimization, and machine learning.
Open-source initiatives have emerged as crucial enablers of standardization. Projects like Quantum Open Source Foundation (QOSF) and Quantum Benchmark Suite provide community-developed benchmarking tools that implement emerging standards, allowing researchers to evaluate their algorithms against established baselines. These tools typically include precision metrics such as quantum volume, circuit layer operations per second (CLOPS), and application-specific error rates.
The convergence of these standardization efforts is gradually creating a common language for discussing and evaluating quantum algorithm precision, enabling more meaningful comparisons between different approaches and accelerating progress toward practical quantum advantage.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!