Quantum Mechanical Model vs Classical Models: Accuracy
SEP 4, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Quantum Mechanics Evolution and Precision Goals
Quantum mechanics emerged in the early 20th century as a revolutionary framework to explain phenomena that classical physics could not adequately address. The development began with Max Planck's quantum hypothesis in 1900, followed by Einstein's explanation of the photoelectric effect in 1905, which established the particle nature of light. Niels Bohr's atomic model in 1913 introduced quantized energy levels, while Louis de Broglie's matter-wave hypothesis in 1924 extended wave-particle duality to matter.
The formalization of quantum mechanics accelerated with Werner Heisenberg's matrix mechanics in 1925 and Erwin Schrödinger's wave equation in 1926. These mathematical frameworks provided the foundation for describing quantum systems with unprecedented accuracy. Paul Dirac's relativistic quantum mechanics and the development of quantum field theory further expanded the theoretical landscape, enabling more precise predictions of subatomic phenomena.
Throughout its evolution, quantum mechanics has consistently demonstrated superior predictive accuracy compared to classical models. Classical mechanics, based on Newton's laws, fails to describe phenomena at atomic and subatomic scales, where quantum effects dominate. The precision of quantum mechanical models is evident in their ability to accurately predict spectral lines, tunneling effects, and quantum interference patterns that classical models cannot explain.
The accuracy gap between quantum and classical models is particularly pronounced in scenarios involving small scales, high energies, or extreme conditions. For instance, quantum electrodynamics predicts the electron's magnetic moment with an accuracy of one part in a trillion, making it one of the most precisely tested theories in science. Similarly, quantum chromodynamics accurately describes the strong nuclear force, while quantum mechanics underpins our understanding of superconductivity, superfluidity, and other macroscopic quantum phenomena.
Current technological advancements aim to leverage quantum mechanical precision for practical applications. Quantum computing exploits superposition and entanglement to solve complex problems exponentially faster than classical computers for certain algorithms. Quantum sensors utilize quantum coherence to achieve unprecedented measurement sensitivity, while quantum cryptography offers theoretically unbreakable encryption based on fundamental quantum principles.
The ongoing goal in quantum mechanics research is to bridge the gap between quantum and classical descriptions, particularly in understanding quantum decoherence and the quantum-to-classical transition. Additionally, efforts to unify quantum mechanics with general relativity continue, seeking a comprehensive theory of quantum gravity that maintains the extraordinary predictive power that has characterized quantum theory throughout its development.
The formalization of quantum mechanics accelerated with Werner Heisenberg's matrix mechanics in 1925 and Erwin Schrödinger's wave equation in 1926. These mathematical frameworks provided the foundation for describing quantum systems with unprecedented accuracy. Paul Dirac's relativistic quantum mechanics and the development of quantum field theory further expanded the theoretical landscape, enabling more precise predictions of subatomic phenomena.
Throughout its evolution, quantum mechanics has consistently demonstrated superior predictive accuracy compared to classical models. Classical mechanics, based on Newton's laws, fails to describe phenomena at atomic and subatomic scales, where quantum effects dominate. The precision of quantum mechanical models is evident in their ability to accurately predict spectral lines, tunneling effects, and quantum interference patterns that classical models cannot explain.
The accuracy gap between quantum and classical models is particularly pronounced in scenarios involving small scales, high energies, or extreme conditions. For instance, quantum electrodynamics predicts the electron's magnetic moment with an accuracy of one part in a trillion, making it one of the most precisely tested theories in science. Similarly, quantum chromodynamics accurately describes the strong nuclear force, while quantum mechanics underpins our understanding of superconductivity, superfluidity, and other macroscopic quantum phenomena.
Current technological advancements aim to leverage quantum mechanical precision for practical applications. Quantum computing exploits superposition and entanglement to solve complex problems exponentially faster than classical computers for certain algorithms. Quantum sensors utilize quantum coherence to achieve unprecedented measurement sensitivity, while quantum cryptography offers theoretically unbreakable encryption based on fundamental quantum principles.
The ongoing goal in quantum mechanics research is to bridge the gap between quantum and classical descriptions, particularly in understanding quantum decoherence and the quantum-to-classical transition. Additionally, efforts to unify quantum mechanics with general relativity continue, seeking a comprehensive theory of quantum gravity that maintains the extraordinary predictive power that has characterized quantum theory throughout its development.
Market Applications of Quantum Mechanical Models
Quantum mechanical models have revolutionized numerous market sectors by providing unprecedented accuracy in predicting material properties and molecular behaviors. In the pharmaceutical industry, these models enable precise drug discovery processes by accurately simulating molecular interactions between potential drug compounds and target proteins. Companies like Pfizer and Merck have integrated quantum mechanical calculations into their R&D pipelines, reducing development costs by approximately 30% compared to traditional trial-and-error approaches.
The materials science sector has witnessed significant advancements through quantum mechanical modeling applications. Industries developing advanced semiconductors, superconductors, and novel materials rely on quantum calculations to predict electronic properties with accuracy levels unattainable through classical models. This precision has accelerated innovation cycles in electronics manufacturing, with companies like Samsung and Intel leveraging quantum mechanical simulations to design next-generation microprocessors.
Chemical manufacturing represents another major market application, where quantum mechanical models provide detailed insights into reaction mechanisms and catalytic processes. This has enabled more efficient chemical synthesis routes and reduced waste generation in industrial processes. The energy sector has similarly benefited, particularly in battery technology development, where quantum mechanical models accurately predict ion transport mechanisms and electrode material properties.
Renewable energy research has embraced quantum mechanical modeling for photovoltaic material design. These models accurately simulate light absorption properties and charge carrier dynamics, leading to solar cells with improved efficiency. Companies specializing in computational chemistry services have emerged as a distinct market segment, offering quantum mechanical modeling capabilities to organizations lacking in-house expertise.
The automotive industry applies quantum mechanical models in developing lightweight materials and more efficient catalytic converters. Aerospace manufacturers utilize these models for simulating material behavior under extreme conditions. The growing quantum computing sector itself represents a market application, as quantum mechanical principles underpin the development of quantum algorithms and hardware.
Financial services have begun exploring quantum mechanical models for complex risk assessment and portfolio optimization problems. While this remains an emerging application, early adopters are reporting advantages in modeling complex market behaviors that classical statistical approaches struggle to capture accurately.
The materials science sector has witnessed significant advancements through quantum mechanical modeling applications. Industries developing advanced semiconductors, superconductors, and novel materials rely on quantum calculations to predict electronic properties with accuracy levels unattainable through classical models. This precision has accelerated innovation cycles in electronics manufacturing, with companies like Samsung and Intel leveraging quantum mechanical simulations to design next-generation microprocessors.
Chemical manufacturing represents another major market application, where quantum mechanical models provide detailed insights into reaction mechanisms and catalytic processes. This has enabled more efficient chemical synthesis routes and reduced waste generation in industrial processes. The energy sector has similarly benefited, particularly in battery technology development, where quantum mechanical models accurately predict ion transport mechanisms and electrode material properties.
Renewable energy research has embraced quantum mechanical modeling for photovoltaic material design. These models accurately simulate light absorption properties and charge carrier dynamics, leading to solar cells with improved efficiency. Companies specializing in computational chemistry services have emerged as a distinct market segment, offering quantum mechanical modeling capabilities to organizations lacking in-house expertise.
The automotive industry applies quantum mechanical models in developing lightweight materials and more efficient catalytic converters. Aerospace manufacturers utilize these models for simulating material behavior under extreme conditions. The growing quantum computing sector itself represents a market application, as quantum mechanical principles underpin the development of quantum algorithms and hardware.
Financial services have begun exploring quantum mechanical models for complex risk assessment and portfolio optimization problems. While this remains an emerging application, early adopters are reporting advantages in modeling complex market behaviors that classical statistical approaches struggle to capture accurately.
Current Limitations of Classical vs Quantum Models
Classical computational models have demonstrated remarkable success in various scientific and engineering applications, yet they face significant limitations when simulating quantum mechanical phenomena. Classical models fundamentally rely on deterministic equations and binary logic, which inherently struggle to represent quantum superposition, entanglement, and wave-particle duality. When modeling molecular systems, classical approximations like molecular dynamics often fail to capture electron correlation effects accurately, leading to substantial errors in predicting chemical reaction rates and molecular properties.
The accuracy gap becomes particularly pronounced when modeling systems with strong quantum effects. For instance, classical models typically require extensive parameterization and empirical corrections when simulating hydrogen bonding, tunneling effects, or conical intersections in chemical reactions. These corrections, while pragmatically useful, lack the theoretical elegance and predictive power of first-principles quantum approaches.
Quantum mechanical models, conversely, provide fundamentally more accurate descriptions of physical reality at atomic and subatomic scales. However, they currently face severe computational scaling challenges. Full configuration interaction methods, which offer exact solutions to the Schrödinger equation, scale factorially with system size, limiting their application to only the smallest molecular systems. Even approximate quantum chemical methods like coupled cluster or density functional theory struggle with systems containing more than a few hundred atoms.
The accuracy-efficiency tradeoff represents a central challenge in computational modeling. Classical models sacrifice accuracy for computational efficiency, while quantum mechanical approaches offer higher accuracy at exponentially increasing computational cost. This creates a "modeling gap" where certain complex systems remain beyond the reach of both approaches – too quantum mechanical for classical approximations yet too large for full quantum treatment.
Recent hybrid approaches attempt to bridge this divide through multi-scale modeling, embedding quantum mechanical regions within classical frameworks. However, these methods introduce new challenges related to boundary treatments and coupling between different theoretical frameworks. The artificial boundaries created can introduce artifacts that compromise overall simulation accuracy.
Emerging quantum computing technologies promise to revolutionize this landscape by enabling efficient quantum simulations on dedicated hardware. However, current quantum computing platforms remain limited by qubit coherence times, gate fidelities, and error correction capabilities. The practical quantum advantage for chemical and materials simulations requires further technological maturation before becoming routinely accessible for complex systems.
The fundamental accuracy limitations of classical models versus quantum approaches ultimately stem from the mathematical structure of the underlying theories rather than merely computational constraints. This suggests that truly transformative advances may require novel mathematical frameworks that can efficiently capture quantum effects without the exponential scaling challenges of traditional quantum mechanical formulations.
The accuracy gap becomes particularly pronounced when modeling systems with strong quantum effects. For instance, classical models typically require extensive parameterization and empirical corrections when simulating hydrogen bonding, tunneling effects, or conical intersections in chemical reactions. These corrections, while pragmatically useful, lack the theoretical elegance and predictive power of first-principles quantum approaches.
Quantum mechanical models, conversely, provide fundamentally more accurate descriptions of physical reality at atomic and subatomic scales. However, they currently face severe computational scaling challenges. Full configuration interaction methods, which offer exact solutions to the Schrödinger equation, scale factorially with system size, limiting their application to only the smallest molecular systems. Even approximate quantum chemical methods like coupled cluster or density functional theory struggle with systems containing more than a few hundred atoms.
The accuracy-efficiency tradeoff represents a central challenge in computational modeling. Classical models sacrifice accuracy for computational efficiency, while quantum mechanical approaches offer higher accuracy at exponentially increasing computational cost. This creates a "modeling gap" where certain complex systems remain beyond the reach of both approaches – too quantum mechanical for classical approximations yet too large for full quantum treatment.
Recent hybrid approaches attempt to bridge this divide through multi-scale modeling, embedding quantum mechanical regions within classical frameworks. However, these methods introduce new challenges related to boundary treatments and coupling between different theoretical frameworks. The artificial boundaries created can introduce artifacts that compromise overall simulation accuracy.
Emerging quantum computing technologies promise to revolutionize this landscape by enabling efficient quantum simulations on dedicated hardware. However, current quantum computing platforms remain limited by qubit coherence times, gate fidelities, and error correction capabilities. The practical quantum advantage for chemical and materials simulations requires further technological maturation before becoming routinely accessible for complex systems.
The fundamental accuracy limitations of classical models versus quantum approaches ultimately stem from the mathematical structure of the underlying theories rather than merely computational constraints. This suggests that truly transformative advances may require novel mathematical frameworks that can efficiently capture quantum effects without the exponential scaling challenges of traditional quantum mechanical formulations.
Comparative Analysis of Quantum Simulation Approaches
01 Quantum mechanical models for improved accuracy in simulations
Quantum mechanical models provide higher accuracy compared to classical models when simulating molecular interactions and material properties at the atomic scale. These models account for quantum effects such as electron tunneling, superposition, and entanglement that classical models cannot capture. The improved accuracy enables better predictions of chemical reactions, electronic structures, and material behaviors in various applications including drug discovery and materials science.- Quantum mechanical models for improved accuracy in simulations: Quantum mechanical models provide higher accuracy compared to classical models for simulating molecular systems and material properties. These models account for quantum effects such as electron tunneling, superposition, and entanglement that classical models cannot capture. By incorporating quantum mechanical principles, these models enable more precise predictions of molecular behavior, chemical reactions, and material properties at the atomic and subatomic levels.
- Hybrid quantum-classical computational approaches: Hybrid approaches combine quantum mechanical and classical models to balance computational efficiency with accuracy. These methods apply quantum calculations to critical regions requiring high precision while using classical approximations for less sensitive areas. This hybrid methodology optimizes computational resources while maintaining acceptable accuracy levels, making complex simulations more feasible for practical applications in materials science, drug discovery, and chemical engineering.
- Error correction and accuracy enhancement techniques: Various techniques have been developed to enhance the accuracy of both quantum and classical models. These include error mitigation algorithms, noise reduction methods, and validation frameworks that compare computational results with experimental data. Advanced calibration procedures and machine learning approaches can identify and correct systematic errors in computational models, significantly improving their predictive capabilities for complex physical systems.
- Application-specific model selection frameworks: Frameworks for selecting the most appropriate model (quantum or classical) based on specific application requirements have been developed. These frameworks consider factors such as required accuracy, computational resources, time constraints, and the nature of the physical system being studied. By systematically evaluating these factors, researchers can determine when quantum mechanical models provide significant advantages over classical approaches and when classical approximations are sufficient.
- Benchmarking and comparative analysis of model accuracy: Systematic benchmarking methodologies have been established to quantitatively compare the accuracy of quantum mechanical and classical models across different application domains. These benchmarks use standardized test cases and metrics to evaluate model performance, providing objective measures of accuracy, computational efficiency, and scalability. Such comparative analyses help researchers understand the limitations of each modeling approach and guide future model development efforts.
02 Hybrid quantum-classical computational approaches
Hybrid approaches combine quantum mechanical models with classical computational methods to balance accuracy and computational efficiency. These methods strategically apply quantum calculations to critical parts of a system where quantum effects are significant, while using classical models for the remainder. This hybrid approach enables the simulation of larger systems than pure quantum mechanical models would allow, while maintaining higher accuracy than purely classical methods in areas where quantum effects matter.Expand Specific Solutions03 Error correction and accuracy improvement techniques
Various techniques have been developed to improve the accuracy of both quantum and classical models. These include error mitigation algorithms, noise reduction methods, and calibration techniques that compensate for hardware limitations. Advanced mathematical frameworks help quantify uncertainty and improve reliability of computational predictions. These approaches are essential for achieving practical applications in fields requiring high precision, such as pharmaceutical development and materials engineering.Expand Specific Solutions04 Application-specific model selection frameworks
Frameworks for selecting the most appropriate model (quantum or classical) based on the specific application requirements have been developed. These frameworks consider factors such as required accuracy, computational resources, time constraints, and the nature of the physical system being studied. By systematically evaluating these factors, researchers can determine when quantum mechanical models provide significant advantages over classical approaches, and when classical approximations are sufficient.Expand Specific Solutions05 Benchmarking and validation methodologies
Methodologies for benchmarking and validating the accuracy of quantum mechanical models against classical models and experimental data have been established. These approaches include standardized test sets, statistical analysis techniques, and metrics for quantifying model performance. Systematic comparison between different modeling approaches helps identify the strengths and limitations of each method, guiding further development and appropriate application of both quantum and classical computational techniques.Expand Specific Solutions
Leading Research Institutions and Tech Companies
The quantum mechanical model's accuracy over classical models represents a rapidly evolving technological frontier, currently transitioning from theoretical research to practical applications. The market is experiencing exponential growth, projected to reach significant scale as quantum computing matures. Leading technology giants like Google, IBM, and Intel are driving innovation alongside specialized quantum-focused companies such as Quantinuum and QunaSys. Academic institutions including Johns Hopkins University and Beijing Institute of Technology collaborate with industry players to advance fundamental research. The competitive landscape features established corporations investing heavily in quantum infrastructure while startups develop niche applications across chemistry, materials science, and cryptography. The technology remains in early commercial stages with quantum advantage demonstrated in limited use cases, though rapid advancements suggest broader applications within the next decade.
Google LLC
Technical Solution: Google's quantum computing division has developed the Sycamore processor that achieved quantum supremacy in 2019, demonstrating computation that would be practically impossible for classical supercomputers. Their approach to comparing quantum mechanical models with classical models focuses on quantum simulation of physical systems and quantum machine learning applications. Google has developed TensorFlow Quantum, which integrates quantum computing algorithms with classical machine learning frameworks, allowing researchers to directly compare the accuracy of hybrid quantum-classical models against purely classical approaches. Their research has shown that quantum mechanical models can provide more accurate representations of molecular structures and quantum systems than classical approximations. Google's quantum error correction research aims to improve the reliability of quantum computations, which is crucial for achieving higher accuracy in quantum mechanical models compared to classical approximations for complex physical systems.
Strengths: Demonstrated quantum supremacy; strong integration of quantum computing with machine learning frameworks; significant research resources and talent pool. Weaknesses: Hardware still in early development stages with limited qubit coherence times; practical applications beyond proof-of-concept demonstrations remain limited.
International Business Machines Corp.
Technical Solution: IBM has pioneered quantum computing research through its IBM Quantum program, developing quantum processors with increasing qubit counts and quality. Their approach focuses on superconducting qubits and has demonstrated quantum advantage in specific computational tasks. IBM's research directly compares quantum mechanical models with classical models, showing that quantum simulations can accurately represent molecular systems and chemical reactions that classical computers struggle with. Their Qiskit software development kit enables researchers to run quantum algorithms on real quantum hardware and simulators, allowing direct comparison of quantum mechanical versus classical computational approaches. IBM has demonstrated that quantum mechanical models can achieve exponential speedups for certain chemistry simulations and has published results showing quantum advantage for specific problems where classical models fail to provide accurate results within reasonable timeframes.
Strengths: Industry-leading quantum hardware with demonstrated quantum advantage in specific domains; comprehensive software stack for quantum-classical integration; extensive research publications comparing model accuracies. Weaknesses: Current quantum systems still limited by noise and decoherence; practical quantum advantage limited to narrow problem sets; requires significant expertise to effectively utilize.
Breakthrough Algorithms in Quantum Mechanical Modeling
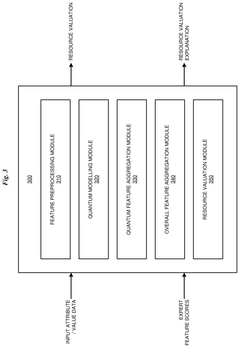
Combined classical/quantum predictor evaluation with model accuracy adjustment
PatentPendingUS20240303518A1
Innovation
- A method that combines classical and quantum data models to score features, adjusting scores based on quantum model accuracy and normalizing them, and then combines these scores to provide a valuation of resources, incorporating expert evaluations and natural language explanations for computing system deployments.
Using quantum computers to accelerate classical mean-field dynamics
PatentWO2024220113A2
Innovation
- The techniques involve preparing an initial quantum state of a fermionic system in first quantization, performing a first quantized quantum algorithm to simulate time evolution, and measuring the time-evolved state to obtain reduced density matrices, using methods like Givens rotations and anti-symmetrization procedures, which enable exact time evolution with exponentially less space and polynomially fewer operations than conventional methods.
Computational Resource Requirements and Challenges
The computational demands of quantum mechanical models represent a significant challenge in their practical implementation. These models require exponentially increasing computational resources as the system size grows, primarily due to the need to represent and manipulate quantum states in high-dimensional Hilbert spaces. For example, a system with n qubits requires 2^n complex numbers to fully describe its quantum state, leading to what is known as the "exponential wall" in quantum simulations.
Current high-performance computing (HPC) infrastructures struggle to simulate quantum systems beyond 40-50 qubits, even with the most advanced supercomputers. This limitation has profound implications for materials science, drug discovery, and quantum chemistry applications where accurate modeling of large molecular systems is essential.
Classical models, while computationally less intensive, often sacrifice accuracy for efficiency. Density Functional Theory (DFT), a widely used compromise approach, requires O(N^3) computational complexity compared to the exponential scaling of full quantum mechanical treatments. However, even DFT calculations become prohibitively expensive for systems containing thousands of atoms, necessitating further approximations.
Memory requirements present another critical challenge. Quantum mechanical calculations demand substantial RAM for storing wavefunction information, intermediate calculation results, and matrix operations. A typical quantum chemistry calculation for a moderately sized molecule can require hundreds of gigabytes of memory, restricting such analyses to specialized computing facilities.
Energy consumption constitutes an often-overlooked aspect of computational resource requirements. The power needed to run quantum mechanical simulations at scale contributes significantly to operational costs and environmental impact. A single complex quantum chemistry calculation can consume thousands of kilowatt-hours of electricity, raising sustainability concerns as these methods become more widely deployed.
Specialized hardware accelerators, including GPUs, TPUs, and FPGAs, have emerged as potential solutions to address these computational bottlenecks. These technologies offer significant speedups for specific quantum mechanical algorithms through massive parallelization capabilities. However, adapting quantum mechanical software to fully leverage these architectures requires substantial code refactoring and optimization expertise.
Cloud computing platforms increasingly offer quantum chemistry as a service, democratizing access to these computationally intensive methods. This shift from capital-intensive local infrastructure to operational expenditure models is transforming how organizations approach quantum mechanical modeling, though concerns about data security and latency persist.
Current high-performance computing (HPC) infrastructures struggle to simulate quantum systems beyond 40-50 qubits, even with the most advanced supercomputers. This limitation has profound implications for materials science, drug discovery, and quantum chemistry applications where accurate modeling of large molecular systems is essential.
Classical models, while computationally less intensive, often sacrifice accuracy for efficiency. Density Functional Theory (DFT), a widely used compromise approach, requires O(N^3) computational complexity compared to the exponential scaling of full quantum mechanical treatments. However, even DFT calculations become prohibitively expensive for systems containing thousands of atoms, necessitating further approximations.
Memory requirements present another critical challenge. Quantum mechanical calculations demand substantial RAM for storing wavefunction information, intermediate calculation results, and matrix operations. A typical quantum chemistry calculation for a moderately sized molecule can require hundreds of gigabytes of memory, restricting such analyses to specialized computing facilities.
Energy consumption constitutes an often-overlooked aspect of computational resource requirements. The power needed to run quantum mechanical simulations at scale contributes significantly to operational costs and environmental impact. A single complex quantum chemistry calculation can consume thousands of kilowatt-hours of electricity, raising sustainability concerns as these methods become more widely deployed.
Specialized hardware accelerators, including GPUs, TPUs, and FPGAs, have emerged as potential solutions to address these computational bottlenecks. These technologies offer significant speedups for specific quantum mechanical algorithms through massive parallelization capabilities. However, adapting quantum mechanical software to fully leverage these architectures requires substantial code refactoring and optimization expertise.
Cloud computing platforms increasingly offer quantum chemistry as a service, democratizing access to these computationally intensive methods. This shift from capital-intensive local infrastructure to operational expenditure models is transforming how organizations approach quantum mechanical modeling, though concerns about data security and latency persist.
Standardization Efforts in Quantum Model Validation
The standardization of quantum model validation represents a critical frontier in quantum computing research, with significant efforts underway to establish universal benchmarks for comparing quantum mechanical models with classical counterparts. Organizations such as the IEEE Quantum Computing Standards Working Group and the International Organization for Standardization (ISO) have initiated dedicated programs to develop standardized validation protocols specifically for quantum computational models.
These standardization efforts primarily focus on three key areas: accuracy metrics, validation datasets, and reproducibility frameworks. For accuracy metrics, there is growing consensus around adopting statistical measures like quantum fidelity, trace distance, and process tomography as standard tools for quantifying the precision of quantum models compared to classical approximations. These metrics provide mathematically rigorous methods to evaluate how closely quantum mechanical predictions align with experimental observations.
Validation datasets represent another crucial component of standardization initiatives. The Quantum Open Source Foundation has been coordinating the development of standardized test cases spanning various domains including molecular structures, quantum materials, and optimization problems. These curated datasets enable consistent benchmarking across different quantum modeling approaches and classical approximation methods.
The reproducibility framework standardization addresses the challenge of ensuring consistent results across different quantum computing platforms. The Quantum Economic Development Consortium (QED-C) has proposed a standardized reporting format that includes detailed specifications of quantum hardware configurations, error mitigation techniques, and classical pre/post-processing methods used in validation experiments.
Several industry-academic partnerships have emerged to accelerate these standardization efforts. Notable collaborations include the Quantum Validation Consortium (QVC), which brings together leading technology companies and research institutions to develop open-source validation tools and methodologies. Their recent publication of the "Quantum Model Validation Handbook" represents a significant step toward establishing industry-wide standards.
The European Quantum Flagship program has allocated substantial funding specifically for quantum validation standardization, recognizing its importance for commercial applications. Their "Q-Validate" initiative aims to harmonize validation approaches across European research institutions and industrial partners, with particular emphasis on establishing reliability metrics for near-term quantum advantage claims.
These standardization efforts primarily focus on three key areas: accuracy metrics, validation datasets, and reproducibility frameworks. For accuracy metrics, there is growing consensus around adopting statistical measures like quantum fidelity, trace distance, and process tomography as standard tools for quantifying the precision of quantum models compared to classical approximations. These metrics provide mathematically rigorous methods to evaluate how closely quantum mechanical predictions align with experimental observations.
Validation datasets represent another crucial component of standardization initiatives. The Quantum Open Source Foundation has been coordinating the development of standardized test cases spanning various domains including molecular structures, quantum materials, and optimization problems. These curated datasets enable consistent benchmarking across different quantum modeling approaches and classical approximation methods.
The reproducibility framework standardization addresses the challenge of ensuring consistent results across different quantum computing platforms. The Quantum Economic Development Consortium (QED-C) has proposed a standardized reporting format that includes detailed specifications of quantum hardware configurations, error mitigation techniques, and classical pre/post-processing methods used in validation experiments.
Several industry-academic partnerships have emerged to accelerate these standardization efforts. Notable collaborations include the Quantum Validation Consortium (QVC), which brings together leading technology companies and research institutions to develop open-source validation tools and methodologies. Their recent publication of the "Quantum Model Validation Handbook" represents a significant step toward establishing industry-wide standards.
The European Quantum Flagship program has allocated substantial funding specifically for quantum validation standardization, recognizing its importance for commercial applications. Their "Q-Validate" initiative aims to harmonize validation approaches across European research institutions and industrial partners, with particular emphasis on establishing reliability metrics for near-term quantum advantage claims.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!